


从根节点开始:
结点1的位置: { NULL }
结点2的位置: { 左 }
结点3的位置: { 右 }
结点4的位置: { 左,左 }
结点5的位置: { 左,右 }
结点6的位置: { 右,左 }
结点7的位置: { 右,右 }
结点8的位置: { 左,左,左 }
结点9的位置: { 左,左,右 }
结点10的位置: { 左,右,左 }
指路法通过根节点与目标结点的相对位置进行定位,可以通过避开二叉树递归的性质“线性”定位,,在C语言中,我们可以利用bit位进行指路,如下:
1 #define BT_LEFT 0
2 #define BT_RIGHT 1
3 typedef unsigned long long BTPos;
二叉树的存储结构是怎么样的呢?用结构体来定义二叉树的指针域,二叉树的头结点也可以用结构体来实现。
结点指针域定义如下:
1 typedef struct _tag_BTreeNode BTreeNode;
2 struct _tag_BTreeNode
3 {
4 BTreeNode* left;
5 BTreeNode* right;
6 };
头结点定义如下:
1 typedef struct _tag_BTree TBTree;
2 struct _tag_BTree
3 {
4 int count;
5 BTreeNode* root;
6 };
数据元素定义示例如下:
1 struct Node
2 {
3 BTreeNode header;
4 char v;
5 };
二叉树的操作
定位如下:
1 while( ( count > 0 ) && ( current != NULL ) )
2 {
3 bit = pos & 1;
4 pos = pos >>1;
5
6 count--;
7
8 parent = current;
9
10 if( bit == BT_LEFT )
11 {
12 current = current -> left;
13 }
14 elsf if( bit == BT_RIGHT )
15 {
16 current = current -> right;
17 }
18 }
二叉树的实现,代码如下:

1 #include <stdio.h>
2 #include <stdlib.h>
3 #include "BTree.h"
4
5 struct Node
6 {
7 BTreeNode header;
8 char v;
9 };
10
11 void printf_data(BTreeNode* node)
12 {
13 if( node != NULL )
14 {
15 printf("%c", ((struct Node*)node)->v);
16 }
17 }
18
19 int main(int argc, char *argv[])
20 {
21 BTree* tree = BTree_Create();
22
23 struct Node n1 = {{NULL, NULL}, 'A'};
24 struct Node n2 = {{NULL, NULL}, 'B'};
25 struct Node n3 = {{NULL, NULL}, 'C'};
26 struct Node n4 = {{NULL, NULL}, 'D'};
27 struct Node n5 = {{NULL, NULL}, 'E'};
28 struct Node n6 = {{NULL, NULL}, 'F'};
29
30 BTree_Insert(tree, (BTreeNode*)&n1, 0, 0, 0);
31 BTree_Insert(tree, (BTreeNode*)&n2, 0x00, 1, 0);
32 BTree_Insert(tree, (BTreeNode*)&n3, 0x01, 1, 0);
33 BTree_Insert(tree, (BTreeNode*)&n4, 0x00, 2, 0);
34 BTree_Insert(tree, (BTreeNode*)&n5, 0x02, 2, 0);
35 BTree_Insert(tree, (BTreeNode*)&n6, 0x02, 3, 0);
36
37 printf("Height: %d\n", BTree_Height(tree));
38 printf("Degree: %d\n", BTree_Degree(tree));
39 printf("Count: %d\n", BTree_Count(tree));
40 printf("Position At (0x02, 2): %c\n", ((struct Node*)BTree_Get(tree, 0x02, 2))->v);
41 printf("Full Tree: \n");
42
43 BTree_Display(tree, printf_data, 4, '-');
44
45 BTree_Delete(tree, 0x00, 1);
46
47 printf("After Delete B: \n");
48 printf("Height: %d\n", BTree_Height(tree));
49 printf("Degree: %d\n", BTree_Degree(tree));
50 printf("Count: %d\n", BTree_Count(tree));
51 printf("Full Tree: \n");
52
53 BTree_Display(tree, printf_data, 4, '-');
54
55 BTree_Clear(tree);
56
57 printf("After Clear: \n");
58 printf("Height: %d\n", BTree_Height(tree));
59 printf("Degree: %d\n", BTree_Degree(tree));
60 printf("Count: %d\n", BTree_Count(tree));
61
62 BTree_Display(tree, printf_data, 4, '-');
63
64 BTree_Destroy(tree);
65
66 return 0;
67 }
用Dev—C++实现代码的结构如下图,这里仅供大家参考体会。
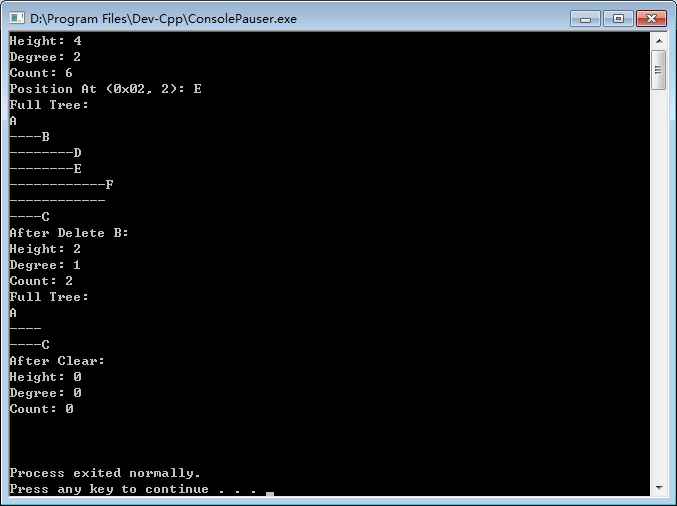
小结:
二叉树在结构上不依赖组织链表;通过指路法可以方便的定位二叉树中的结点;基于指路法的二叉树在插入,删除以及获取操作的实现细节上与单链表相似(单链表就是特殊的二叉树,实现上相似,知识更简单一点啦)
作者: 李肖遥, 来源:面包板社区
链接: https://mbb.eet-china.com/blog/uid-me-3912462.html
版权声明:本文为博主原创,未经本人允许,禁止转载!
 /4
/4 
文章评论(0条评论)
登录后参与讨论