


之前的几章里,大家已经做过不少练习了。现在大家手中的代数工具只有DeMorgen定理和推泡泡定理。那么在设计逻辑门的时候,有很多时候不止一种实现方法,各有不同的优势。那么怎样才能随心所欲的设计逻辑门电路呢。答案就是利用数学工具。数学?!头痛!没关系,只要动手做,就一定能学会。
说明一下,这里的形式采用和讲二进制时候一样。易懂而不罗嗦,以后忘了,来这一看就能想起来。
1。符号定义:和以前的规则一样 ~A 代表 “非”(NOT) A,A+B代表“A或B”(A OR B),A*B代表“A和B”(A AND B)
2. 优先权:和加减乘除类比,布尔代数优先权从高到低为NOT,AND,OR。
例Y=A+BC 等价于:Y=A+(BC)而不是Y=(A+B)C!所以括号用来改变运算优先权。
3.SOP(SumOfProduct)形式:
首先定义最小项(minterm):真值表的每一行一定会有一个使输入以AND组合后为“真”的表达式。。。神马意思,看例子:
这里minterm的组合形式均为AND的形式,观察两个例子中的输入和minterm项,无论输入是什么,minterm都是“1”(真)。
在(1)中,输出为Y为1的时候,minterm只有~AB的形式,所以第一个真值表的表达式是Y=~AB,同理第二个例子的表达式是
Y=~AB+AB。---神奇吧,再也不用一行一行看去找表达式了。没什么了,这是数学的小把戏。其实原理是这样的,我们分析真值表的
时候,只要找出当输出为1的输入组合(AND组合)就可以。因真值表枚举了所有输入进行AND的情况,只有符合Y的值的才可以入选,而逻辑运算除了只有NOT,AND,OR。而一个逻辑回路里,可以有很多输入组合其输出结果为1,所以只要把这些情况相(加)或就能得到表达式。
而(2)得到的表达式就是叫做SOP规范形式(sum of product)~~用来唬人的名字。因为式的意思是 把两个AND的结果相OR(把两个积相加)。
这里大家想起来概率的运算了吗?独立事件神马的。是的有着密切的关联!因为二进制数操作本身就是概率的操作。举例说,有8个空bits,那么我们就有8个位置去放0和1,那么总共的概率就是
2^8=256,也就是有256种放的方法,这不就是8bits的范围嘛(0~255)。所以二进制操作符合概率的计算。再举个例子,Y=~A~B~C+A~B~C+A~BC也是SOP形式。(大家改动手画它的真值表了,然后验证上面讲的!)感觉式子好长吧,画起线路图来很麻烦。
是的,我们这不是在探索捷径呢嘛~
4 POS(ProductOfSum)形式:
和SOP一样,不过先定义最大项(minterm):真值表的每一行一定会有一个使输入以OR组合后为“假”的表达式(原理:真值表枚举了所有输入进行OR的情况,只有符合Y的值的才可以入选),看例子:
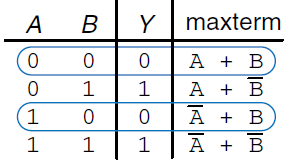 。大家自己用上面SOP的想法一步一步分析。我就不罗嗦了,不懂得留言。这个真值表的表达式即为Y=(A+B)*(~A+B)。
。大家自己用上面SOP的想法一步一步分析。我就不罗嗦了,不懂得留言。这个真值表的表达式即为Y=(A+B)*(~A+B)。
5.布尔代数(Boolean Algerbra)
就是和一般的加减乘除差不多,只比那个更简单。所以大家不要怕噢~。首先我要引入公理和定理的区别:公理不能被证明,而定理可以用一堆公理来证明。
其次就是双对的定义:如果1和0,AND和OR同时交换的时候,结果不变。我们说结果有双对的性质。例如:如果 ~B=1则B=0 和 如果 ~B=0则B=1 这两个描述的都是同一个事情,不过1和0交换了,就是这两个叙述成双对关系。
(如果不明白就跳过,学完之后回来再看一定会懂得)
(a)好了,现在把布尔代数中需要的定义拿出来:
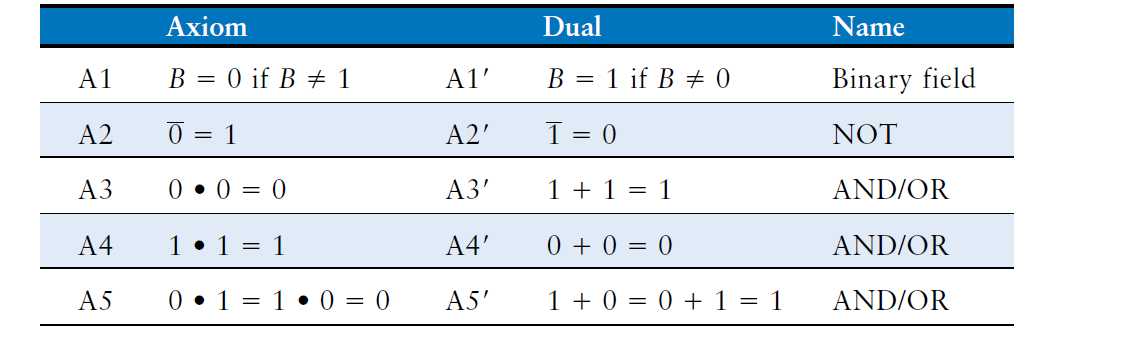 。解释一下:Axiom就是事实,Dual就是从另一个方向描述事实的双对。Name就是这个公理的名字。
。解释一下:Axiom就是事实,Dual就是从另一个方向描述事实的双对。Name就是这个公理的名字。
例如A1说的就是如果B不等于1,则B等于0.也就是说这是二进制领域(见Name)。其双对的描述就是:如果B不等于0则B一定是1.A1'和A1很对称吧~。剩下的一定要一个一个看完。要不继续讲可能会糊涂。
(b)只有一个变量的定理:
 。这里T代表Theorem,也就是可以用(a)里的公理证明的!注意Name里Identity就是代表“自己运算(经过某种运算后和原来相同)”
。这里T代表Theorem,也就是可以用(a)里的公理证明的!注意Name里Identity就是代表“自己运算(经过某种运算后和原来相同)”
数学里也叫 单位运算 。Null Element顾名思义 “零元素”,概念就是和任何数乘0都得0一样。0“与”任意输入都是0,而1或任意输入都是1.Idempotency就是等幂性。说的是,一个输入AND自己一下得到仍是自己,在AND一下还是自己,n次以后还是自己即B^n=B就是无论是几次乘积操作都是等同的(幂就是乘方)。Involution我们早已见过,就是求两次逆的操作。Complements就是互补,一个输入AND自己的互补结果一定是0.因为1的互补是0,0的互补是1..
好了就先写到这,下一结我们看如何如何用这些工具,以及更多变量的时候怎么处理。
 /2
/2 
用户440448 2013-10-12 21:45