原创 【博客大赛】PET系统时间信息之定时

PET系统时间信息之定时

概述

         在《PET系统基础之时间信息概述》一文中介绍了PET系统的时间信息，其实说白了，这个时间信息就是指事件发生的时间，或者说是粒子击中探测器的时间，也可以说是粒子到达时间（arrival time）。问题关键是如何精确地获取这个时间，所以需要精确的定时，在PET系统这个精度至少应该是亚纳秒级的。

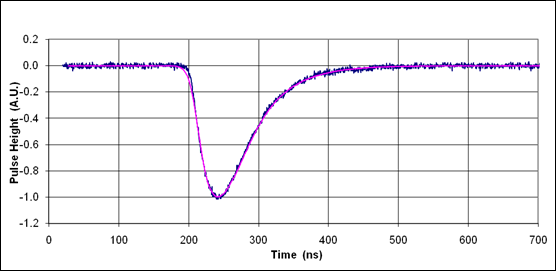
图1：LYSO得到的典型PMT输出脉冲信号

产生时间晃动的几个主要因素

         在《PET系统基础之时间信息概述》一文中提到了arrival time的晃动是导致测量误差重要因素。那么又是什么导致的时间晃动呢，主要有以下几个因素：

1、  探测器的固有晃动。

2、  噪声引起时检点路输出的时间晃动。

3、  幅度时间游动效应。

4、  上升时间游动效应。

以上几种因素在不同条件喜爱对晃动所起的影响是不同的，因为要具体加以分析，分清主次。应着重分析幅度和上升时间游动效应产生的时间晃动及其解决办法。另外，上述列出的因素，主要讨论的是信号调理阶段，也即模拟信号处理。在后端时间量化的时候，也会存在所谓的量化误差（比如TDC误差、时钟Skew和jitter等），这是另外一个概念，这里论述的是时间定时的基础，如果基础不精确也就谈不上后续TDC的测量精度了。

         首先我们来看探测器固有晃动，这是因为不同探测器元件的电流信号输出的时间晃动不一样，产生原因也不相同，大致因为载流子在探测器内运动途径不同造成。至于PET系统，其探测器是PMT，由于伽玛光子击中的位置不同使得光传输到PMT的时间不同，这样其输出信号的时间发生差异，而击中的位置往往是随机的，因为信号输出的时间产生晃动。对于这个因素，目前信号调理电路还没有好的办法应对，只能是在挑选PMT的时候下功夫，另外通过多次试验可以在后端对PMT传输时间进行Time Correction，这个Correction的参数通过大量实验获取，并能随时进行更新，所以现在也基本能保证对探测器固有晃动进行很好的补偿。

         第二个因素是噪声，噪声叠加在信号上会引起时检电路输出的时间晃动，这个需要通过提高调理电路设计来进行处理，这里不展开。

         第三个因素是幅度时间游动效应，探测器输出信号的随机变化造成了时间上晃动，称为幅度时间游动效应。不同幅度经过时检电路之后在输出时间上产生差异，如图2所示。

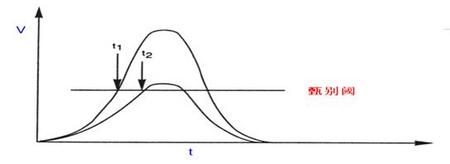
图2：幅度时间游动效应

         最后一个因素就是上升时间游动效应，PMT的输出信号上升存在随机变化，这就带来了时检电路的输出信号在时间上晃动，这称为上升时间游动效应。不同的上升时间的信号经过时间检测电路之后会产生在输出信号时间上的差异，如图3所示。

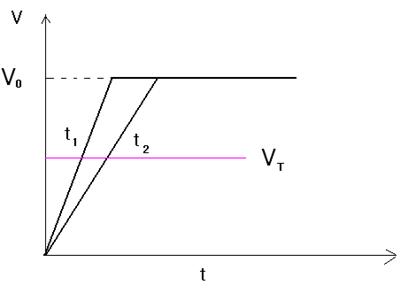
图3：上升时间游动效应

         通过图2和图3，那么我可以假设同一个信号通过不同的PMT那么得到不同的幅度以及不同的上升时间，按图示，我们必然会得到不同的定时，这种定时误差必须通过相应的时间检测电路进行避免。

时间晃动大小的度量

         具体的理论推导公式以及实验不是笔者的重点，相关的参考文件上可以找到详细的内容。这里借用参考材料上推论时间晃动大小度量时做的实验模型来说明另外一个问题。如图3所示，这是参考资料上实验示意框图。

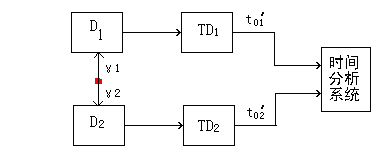
图4：时间晃动实验测量

         这里笔者需要强调的是，图4所示的实验，在PET系统设计中也用得到。一个PET设计完成之后，需要做大量如图4所示的实验，由于PET系统中探测器采用PMT，一个系统有好几百个PMT，尽管PMT采用同一厂家同一批次，但是PMT之间的差异总是存在的，应用图4所示的实验需要获取每一个PMT的光子传输时间信息，有了这些数据才能在后端数字处理的时候进行Time Correction补偿。

前沿定时甄别器-固定阈值甄别器

         甄别器是时间检测电路的核心，传统的方式就是直接对前沿进行甄别，后来发展到双沿甄别。

         首先我们来看所谓的前沿定时特性，如图5（a）所示，假设将输入信号近似看成线性上升，可以用下述关系表示：

V_i(t)=t     0<t<t_m

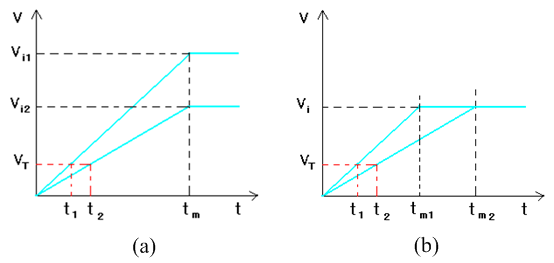
图5：信号前沿

         那么输出信号对输入信号的时间延迟可以表示为：t_d = t_t + t_a，其中t_t为输入信号从出现到上升为V_T所需时间，t_a为渡越时间，假定在快甄别器情况下，t_a很小，暂时不加以考虑。

t_d = t_t = t_m

         在V_i由V_i1变为V_i2时，ΔV_i = （V_i1 – V_i2），如果ΔV_i很小，则输出信号对输入信号的时间延迟差Δt_d = （t₂ – t₁）应为：

Δt_d = t_{m -} t_m = V_T*t_m() =  t_mΔV_i

         t_d随V_i变化而发生变化称为幅度时间游动效应。显而易见V_T和t_m越小，t_d变化量就越小，幅度时间游动效应就越小。

         上面的讨论时假设ΔV_i很小情况下，如果V_i变化很大时，服从某一种分布规律，要得到Δt_d必须V_i的概率密度函数求得t_d的概率密度函数，得到Δt_d。如果达峰时间t_m发生变化（也就是上升时间发生变化），延迟时间的变化为：

Δt_d =  t_m

这就是所谓的上升时间游动效应，如图5（b）所示。实际系统中这两种游动效应都要同时考虑。

         通过以上分析，信号前沿定时会有较大的定时误差。降低甄别阈值，是减少这个误差的重要措施。但是甄别阈值的减少会明显引起噪声误触发，为此设计了双阈甄别电路，利用低阈值来定时，高阈值进行选通的方案，既可以减少噪声影响，又由于甄别阈的降低，还可以减少由于幅度效应引起的时间游动。

         阈值设定通过DAC提供一个阈电压来实现，为了减少噪声和外部的干扰影响，得到稳定的阈电压，对DAC提供的输出电压采取了衰减和有源滤波等有效措施。如图5所示，为双阈甄别电路结构图。

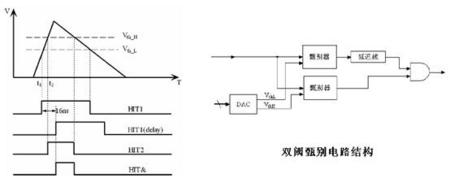
图6：双阈甄别电路结构

         在实际应用中，图6的结构经常出现double trigger的情况，这是因为将低阈值舍得太低，相邻的脉冲被放出去了，同时高阈值设置也不是合理使得这种情况被选通了。如图7所示的紫色通道，两个较宽的方波不是double trigger，这是两个挨得很近的事件形成的两次真触发，但是第二个脉冲后面跟了一个较窄的脉冲就是所谓的double trigger。

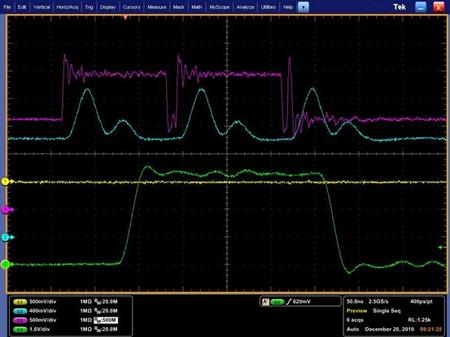
图7：Double trigger

恒比定时甄别器（CFD）

         由于双阈甄别器存在的一些问题，业界目前普遍采用CFD方法来实现甄别器。我们知道前沿定时有由于幅度游动效应引起的较大晃动的缺点，另外触发比不恒定是其另外一个重要缺点。

         另外，根据资料上的理论推导，探测器的固有时间晃动往往与外电路收集到的电荷量与总电荷量比值有关，在某个比值时，固有时间晃动可达到最小。这个比值恰好就是触发比P：

P =

         如果能对每一个信号做到恒定的触发比，就可以选择合适的比值，使得探测器的固有时间晃动最小，同时又能克服幅度游动效应。

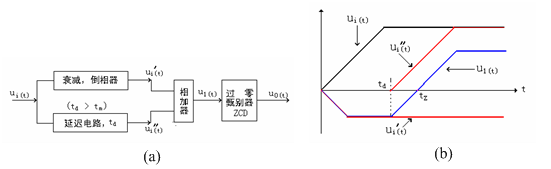
图8：恒比定时（CFD）甄别原理

         如图8-a所示，为CFD的电路原理图。输入信号分成两路，一路经过延迟，另外一路经过衰减并倒相。然后，将这两路信号相加产生一个双极性信号，该信号从负极性变到正极性的过零时刻与信号幅度无关，在此时刻的信号值和总幅度之比为一恒值。过零甄别器起到在双极性信号的过零时刻检出信号的作用。用u_i(t)来近似描述输入信号，那么

u_i(t) =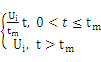

经过衰减倒相后，信号为（其中P为衰减因子）：

u_i’(t)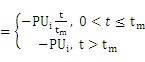

经过延迟后代的信号为：

u_i”(t)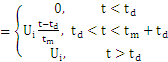

经过相加电路之后，是一个双极性信号：

u₁ (t)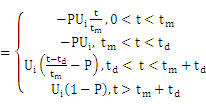

从负极性变到正极性的过零时刻：t_z = t_d + Pt_m

由此可知：

l  过零点与信号幅度无关

l  在t_z时刻，对于任何幅度都一样

因此t_z是一个理想的时刻，既克服了游动效应，又在此时刻的信号值与总幅度之比为一恒定值。在这一时刻检出信号可以达到恒比定时的目的。图7中，过零甄别器ZCD起到在信号过零时刻检出信号的作用。

幅度和上升时间补偿定时（ARC）

         CFD仅仅解决了幅度游动效应，未曾解决上升时间游动效应。ARC定时可以同时解决幅度和上升时间游动效应。ARC的电路结构和CFD完成相同，只是其延迟时间t_d应满足：

t_d < (1 - P)t_m

相加后的输出信号应为：

u₁ (t)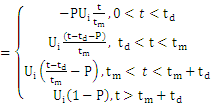

解得：

t_z =

在ARC定时中：

u_i” = ()         u_i’ = ()

对于延迟信号触发比：

f” = ()

对于衰减倒相信号的触发比：

f’ = ()

t_m不是常数时，f”和f’也就不是常数，因此不是真正恒比。

结论

         本文学习了PET系统中时间晃动的几个因素，并分析了产生这些因素，试图找到精确定时的方法。