原创 简介如何计算电路极值和电路统计分析

我们实际分析的电路的时候如果参数比较多，就很难分析到底如何选取参数组合得到最大最小值。这里使用多元偏微分的方法来运算。如果我们需要计算统计的进度，我们可以使用蒙特卡洛方法。
蒙特卡罗(MonteCarlo)方法，或称计算机随机模拟方法，是一种基于“随机数”的计算方法。
下面举个例子来说明吧，把各个参数分成正态分布和均匀分布分别讨论。
加一些说明和注释吧，否则大概看不太明白或者要费很多时间：
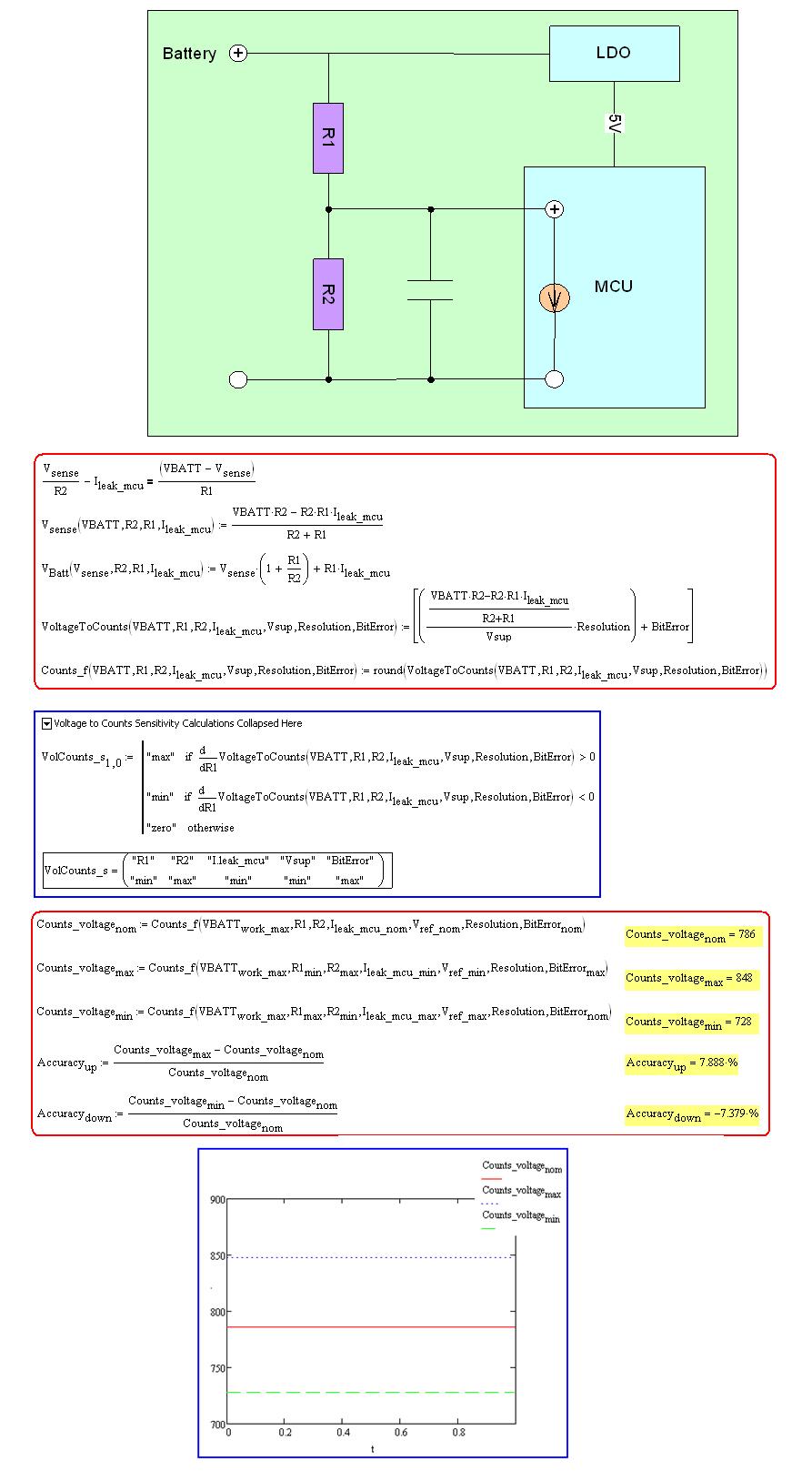
电路很简单，两个电阻分压，由单片机的自带AD采样。
电路的误差因素可以罗列为
电阻R1误差：一般电阻标定的1%为出厂精度，焊接过后，温度变化，温度冲击都会引起变化，在前面的博客中有介绍，具体不详细叙述。
电阻R2误差
Ldo输出电压作为单片机AD参考源产生误差
Ad采样的Bit误差
Ad存在输入电阻产生的漏电流
五个误差因素
然后列公式，首先是到AD口的电压分析，其次是电压转化为数值的分析。合在一起，有五个参数，如何确定最大值，当然你可以自己去分析那个参数对结果的影响。简单的方法是直接对每个参数求偏微分，如果变化区间不大的话，可以直接得出来正影响还是负影响。
然后得到数值变化图，最大值，最小值，正常值。
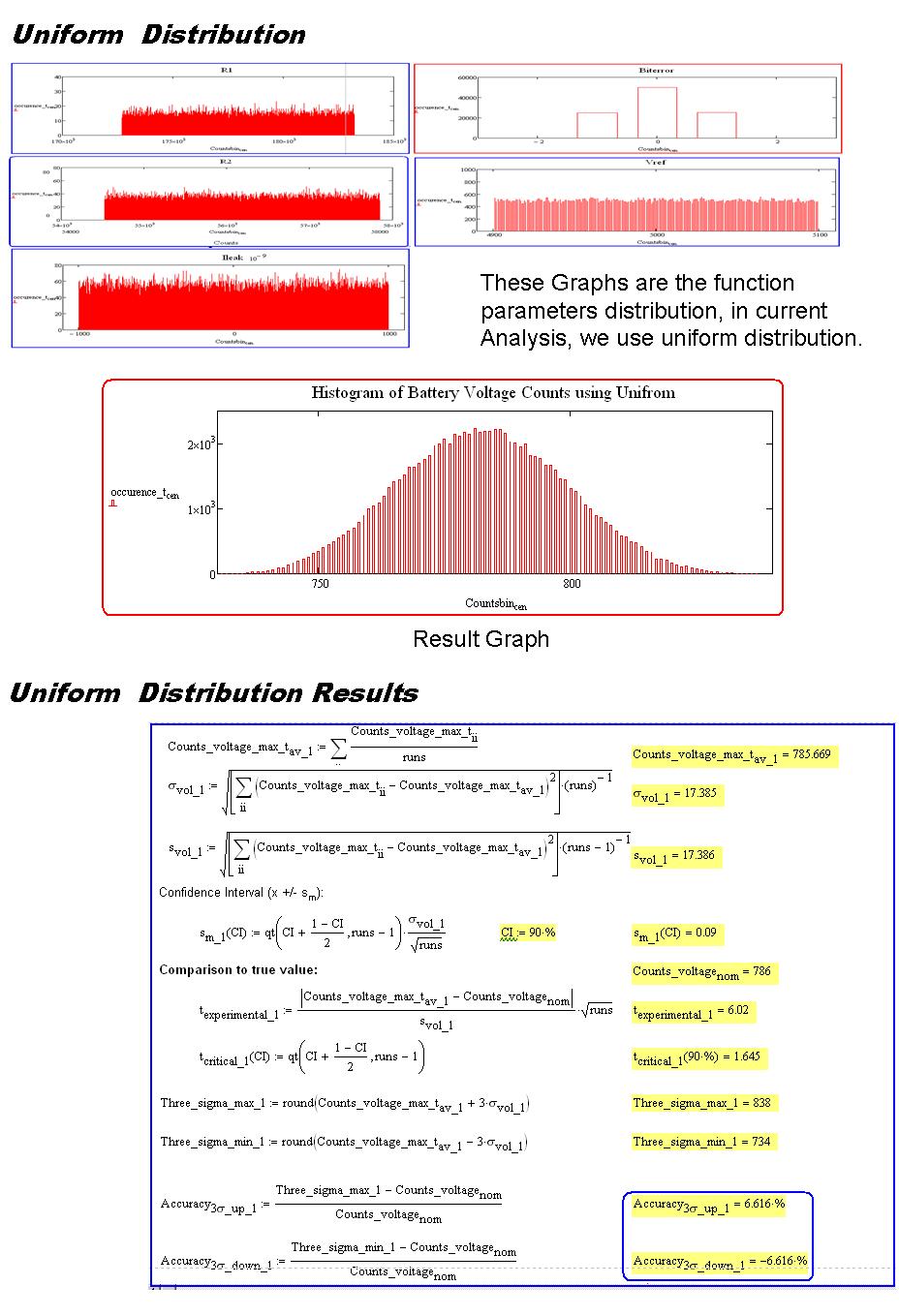
我们来检验一下，设定5万次抽样。
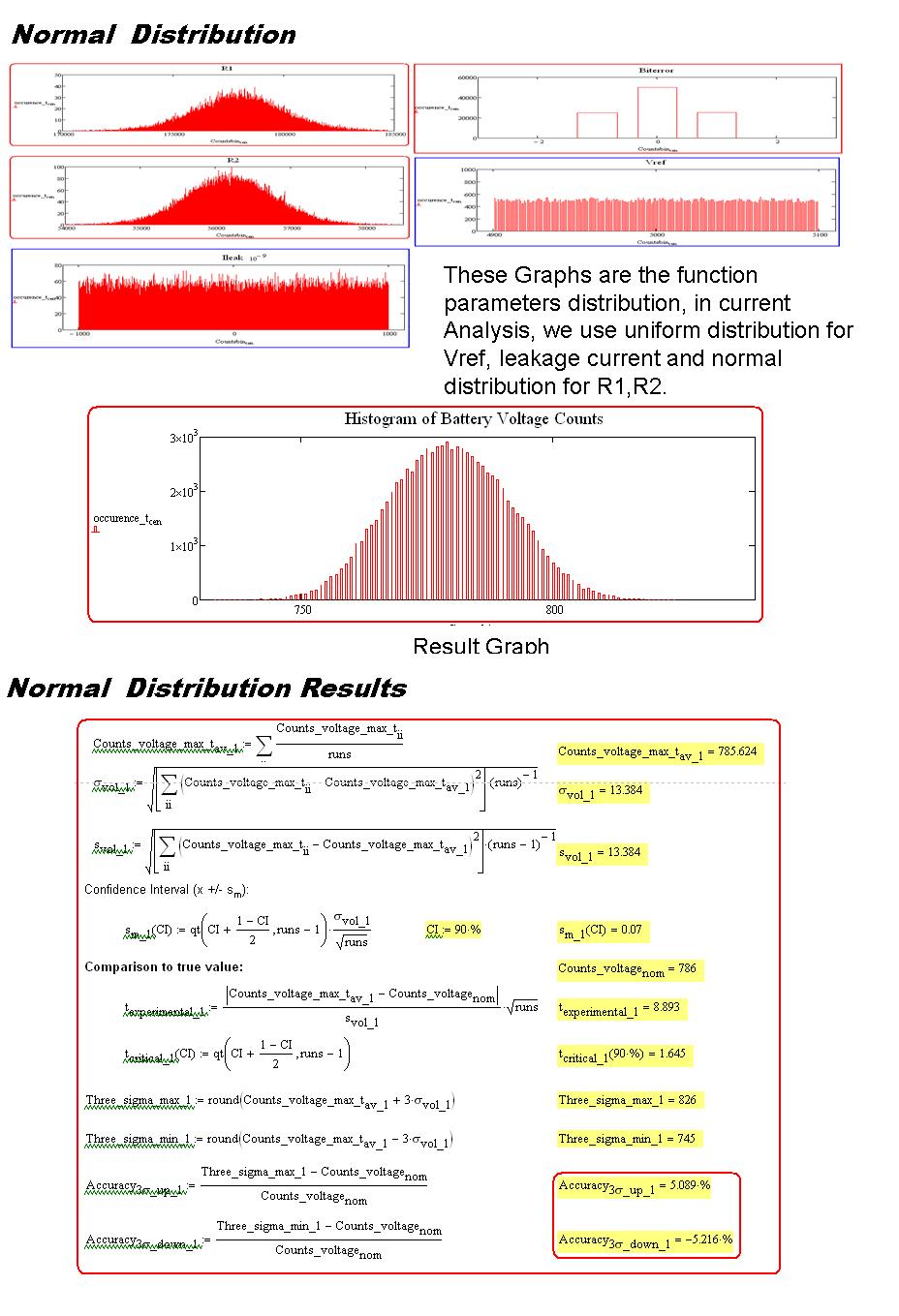
首先把所有的误差设定为平均分布，然后让参数随机产生，得出结果后，按照值的区间来做分布，可以得到曲线分布图。当然得到结果后，可以求出方差和标准差了，可以得到3标准差的精度了。这里只做介绍，以后我会单独拉出来分析分析。
对比误差平均分布和正太分布，可以发现结果差很多。所以如果我们不重视前期验证和设计的话，过个一两年老化，冲击之后，我们的参数都往外偏，可以想象一下我们为什么在实验室好好的，批量出来总会有个把“不听话”的了真正原因了。