原创 优思学院｜置信区间为什么用的是标准误而非标准差？

置信区间反映的是“样本均值”这个统计量的不确定性，因此使用的是标准误（standard error），而不是直接用样本标准差（standard deviation）。标准误体现的是均值的波动程度，而样本标准差体现的是个体数据的波动程度，两者并非一回事，就如下图所显示的一样。

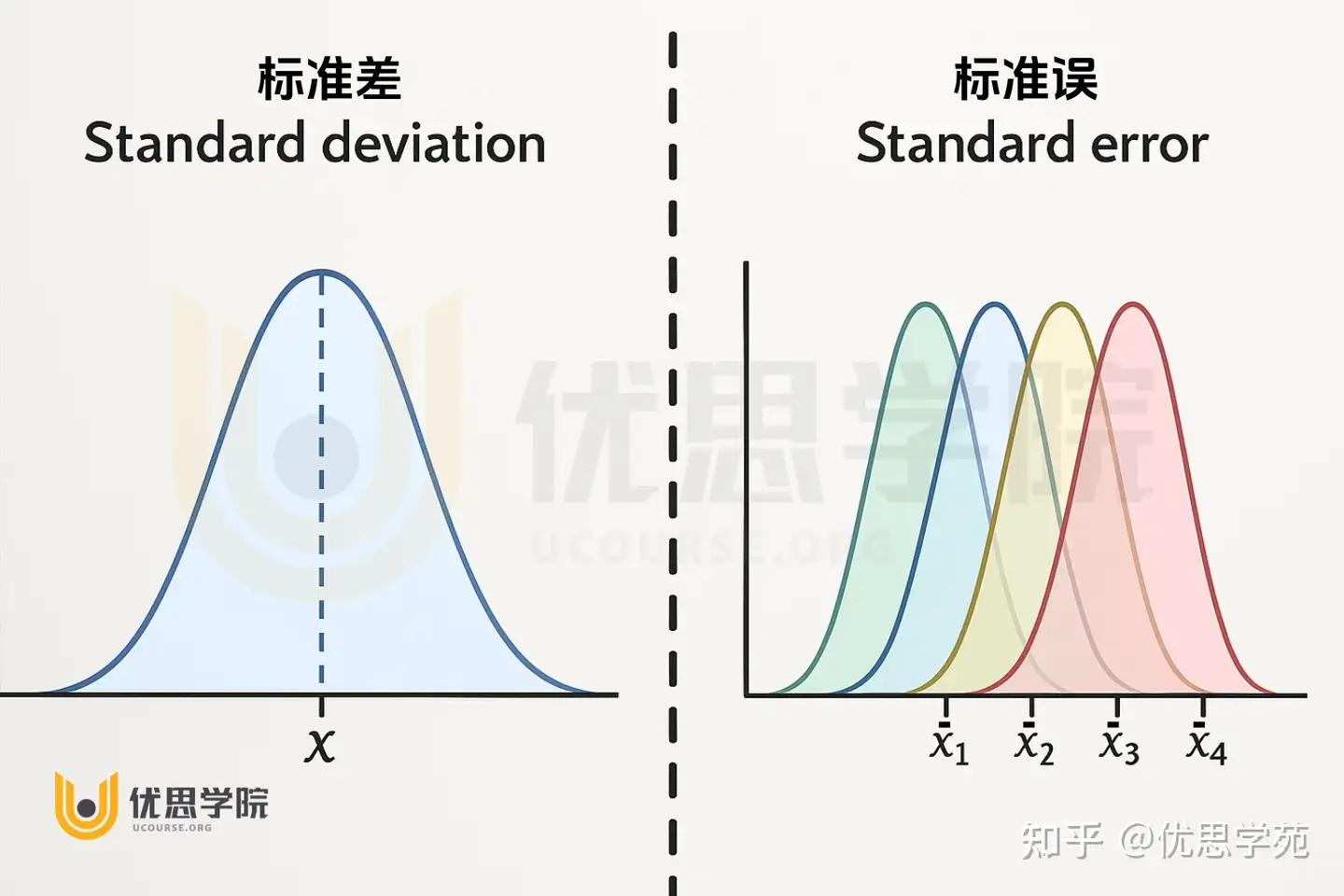
下面优思学院会一步一步解释清楚：

一、标准差和标准误，究竟差在哪？

很多同学对“标准差”和“标准误”这两个概念傻傻分不清楚，但其实差别明显：

• 标准差（Standard Deviation，σ或s）：
  是衡量单个数据点相对于平均值波动的程度，反映的是总体（或样本中每一个个体）数据的波动情况。
  
• 标准误（Standard Error，σ/√n 或 s/√n）：
  衡量的是样本均值这个统计量本身波动的程度，也就是抽取不同样本后得到的样本均值之间的波动程度。

简单来说：

• 标准差：看个体数据的波动
  
• 标准误：看样本均值的波动

两者衡量对象本质不同，因此不能混用。

二、为什么置信区间需要用标准误？

我们回到置信区间的本质来看：

置信区间的目标是什么？

是推测总体参数的范围，比如推测总体均值。这里用到的是“样本均值”这个统计量，而非单个样本数据本身。

由于样本均值每次抽样都会变化，每次抽样得到的均值都会和真实的总体均值存在一定偏差。这种偏差的波动程度，就是用“标准误”来描述的。

举个生动点的例子：

• 假设一个班有50名同学，真实的平均身高是170cm，标准差为10cm。
  
• 你每次随机抽取10个学生，算出一个样本均值，这个均值不会每次都刚好是170cm，可能171cm、168cm、169.5cm……
  
• 你抽很多次样本，每个样本的均值之间是有波动的，这个波动程度就要用标准误来衡量。
  
• 样本容量越大，抽取的样本均值就越接近真实均值（170cm），样本均值之间的波动就越小，因此标准误是 σ/√n，n越大，标准误越小。

因此，置信区间本质上是以样本均值为中心，向外延伸一定范围，来推测总体均值在哪个区间内。
这个向外延伸的范围就必须用标准误来决定，而不是直接用标准差。

三、为什么不能用样本的标准差？

很多同学在做题时发现，给定的是一个样本，样本也是正态分布啊，为啥不用样本自己的标准差呢？

原因是：

• 样本的标准差体现的是单个样本内部个体之间的波动。
  
• 但置信区间关注的是样本均值和总体均值之间的误差波动。

即便你只抽了一个样本，这个样本虽然也近似正态分布，但它的标准差描述的是数据之间的差异，而不是“样本均值”与“总体均值”之间的差异。

再形象一点：

• 一个样本数据的标准差体现的是样本内个体之间的差距；
  
• 但你做推断的时候，关心的是**“我的这个样本均值距离真实的总体均值有多远？”**
  
• 为了回答后面这个问题，你必须用标准误，而非标准差。

四、做题时看到的“σ/√n”和单个样本的关系？

做题时题目一般给你一个样本，常常还会给出总体标准差σ，或者让你用样本标准差s来估计σ（如果σ未知的话）。

题目里出现的：

• 若总体标准差σ已知，你直接用标准误 σ/√n 计算置信区间即可；
  
• 若总体标准差σ未知，那你必须用样本标准差s来替代σ，这种情况下标准误为 s/√n。

无论哪种情况，都必须是 σ/√n 或 s/√n，而不是 σ或s本身。

这和你只拿到一个样本，并不冲突。因为哪怕你只抽了一个样本，你做推断的基础仍然是“样本均值”这个统计量的波动程度，本质不会改变。

总结一下

标准误体现的是样本均值这个统计量的波动，而标准差体现的是个体数据的波动，两者衡量的是完全不同的东西。

置信区间关注的核心是推断总体参数（例如均值）落在哪个区间，因此用到标准误，而非样本本身的标准差。

理解了这一点，统计推断中关于标准差和标准误的问题也就迎刃而解啦！