原创 基于FPGA的数字滤波设计—理论知识1

基于FPGA的数字滤波设计—理论知识

2.1数字滤波基础

2.1.1 数字滤波理论

     数字滤波最明显的优势是几乎消除了无源元件随时间和温度的波动、运算放大器漂移(有源滤波器)等造成的滤波器误差。数字滤波器的特性可以通过软件控制轻松改变，广泛应用于自适应滤波。设计数字滤波器的基本步骤与设计模拟滤波器相同。首先确定所需的频率响应特性，然后计算滤波器参数。模拟滤波器与数字滤波器的主要差别在于：前者计算的是电阻、电容和电感值，而后者计算的是系数值。对于数字滤波器，数值取代了模拟滤波器的电阻和电容等物理元件。这些数值作为滤波器系数保存在存储器中，与来自ADC的数据一起用于执行滤波计算。

数字滤波器的功能就是把输入序列x(n)通过一定的运算变换成输出序列y(n)。不同的运算处理方法决定了滤波器实现结构的不同。

图2.1显示基本数字滤波功能：滤除一个低频信号中的高频噪声。原始波形必须利用一个ADC数字化，产生样本x(n) 。然后将这些数据值馈入数字滤波器。输出数据样本为y(n)，DAC利用它重建一个模拟波形。和模拟滤波器相比，ADC和DAC是新加入部分。

图2.1 基本数字滤波示意图

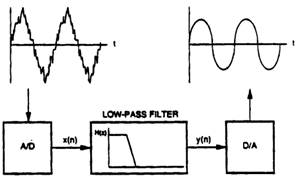
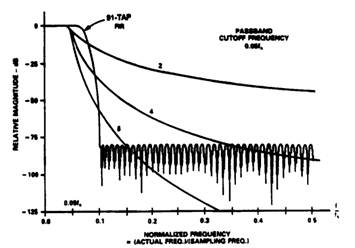
       图2.2显示了91抽头FIR滤波器响应与切比雪夫模拟滤波器响应的对比。一是针对1dB 带内纹波而优化的二阶、四阶、六阶理想切比雪夫低通模拟滤波器；一是针对0.2dB通带纹波而优化的91抽头数字FIR滤波器。可以看出几乎没有与之对应的模拟滤波器，因为硬件无法实现如此高阶的模拟滤波。FIR滤波器通带内的响应更平坦，通带内的相位失真可忽略不计，因为滤波器将所有频率成分均等延迟。

         图2.2数字滤波器和模拟滤波器的比较

从以上分析可以看出，数字滤波和模拟滤波相比优势在于如下几点：

1、  线性相位、恒定的群延时（FIR）；

2、  无器件变化导致的漂移；

3、  灵活，可实现自适应滤波；

4、  易于仿真和设计。

数字滤波存在的限制：

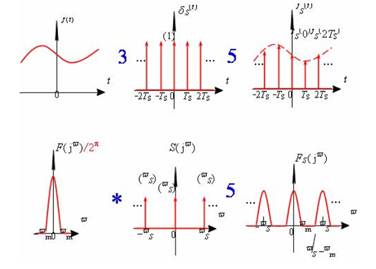
1、  仍然需要模拟滤波器用来抗混叠和高频处理（离散带来的频谱重复，如图2.3所示）；

2、  至少需要ADC器件，有时还需要DAC器件恢复模拟信号；

3、  对于高带宽信号，缺少高速ADC对其进行采样。

图2.3 离散后的频谱重复

2.1.2 FIR理论

FIR滤波器之所以得名为有限脉冲响应(FIR)滤波器，是因其脉冲响应的持续时间是有限的。也就是说：对于N阶FIR滤波器，在输入N个零值输入样本后，滤波器输出一定为0。如图2.4所示。

FIR计算公式（差分方程）：

                                                                                                                (2-1)

硬件实现结构：

图2.5  FIR实现的基本结构

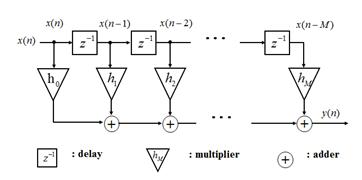
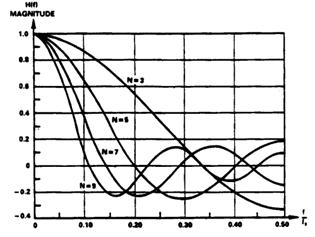
       提高抽头数N可以使FIR滤波器的滚降特性发生更急剧的变化（如图2.6所示），阻带衰减特性可以通过适当地选择滤波器系数来改善。FIR滤波器设计的本质在于选择合适的滤波器系数和抽头数，从而实现所需的频率传递函数（频率响应）H(f)。有多种算法可将频率响应H(f)转换成一组FIR系数h(n)（可直接利用MATLAB工具）。所以我们设计的重点是，把需求转化为频率响应H(f)。

图2.6抽头数对滤波器的影响

       FIR滤波器设计的关键法则是：FIR滤波器的系数h(n) 等于频率传递函数H(f) 的脉冲响应的量化值。反之，脉冲响应为H(f)的傅里叶变换。

在数字采样系统中，卷积运算可以通过一系列乘法和累加来实现。时域/频域中的卷积运算相当于频域/时域中的点与点乘法。从图2.7可以看出，频域中的滤波可以通过如下方式完成：将通带中的所有频率成分乘以1，并将阻带中的所有频率成分乘以0。即频域中的乘法，相当于时域中的卷积。反之，频域中的卷积相当于时域中的点与点乘法。

频域中的传递函数可以通过傅里叶变换转换到时域，这种变换会在时域中产生一个脉冲响应。由于频域中的乘法(信号频谱乘以传递函数)相当于时域中的卷积(信号与脉冲响应卷积)，因此可以将信号与脉冲响应卷积，从而对信号进行滤波。FIR滤波正是这样一个过程。

在连续时间系统中，拉普拉斯变换可以看作是傅里叶变换的一般情形。同样，可以对离散时间数据采样系统的傅里叶变换进行一般化处理，得到所谓z变换。

         图2.7时域和频域的对偶性

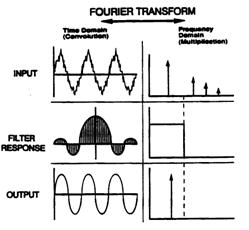
FIR滤波器设计关键：

1、  FIR 滤波器的系数h(n) 等于频率传递函数H(f ) 的脉冲响应的量化值。

2、  通过对H(f ) 进行傅里叶变换来计算脉冲响应。