原创 基于FPGA的数字滤波设计—理论知识2

基于FPGA的数字滤波设计—理论知识2

2.1.3 IIR理论

和FIR滤波器相比，IIR滤波器有对应的传统模拟滤波器(巴特沃兹、切比雪夫和椭圆滤波器)，并且可以利用我们更熟悉的传统滤波器设计技术进行分析和合成。

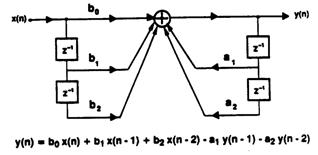
图2.8(a) 显示了一个模拟压控电压源低通滤波器，属于Sallen-Key 复极点拓扑结构，其对应的IIR数字滤波器如图2.8(b)所示。该二阶IIR滤波器称为“双二阶滤波器” (因为它是利用z域中的一个双二阶方程式来描述)，是更高阶IIR设计的基本构建模块。图中还给出了描述具有5个系数的该滤波器特性的差分方程。

(a)二阶低通有源滤波器

(b)对应的IIR滤波器

图2.8模拟滤波器和IIR对应关系

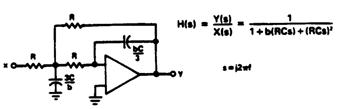
IIR滤波器系统函数表示为：

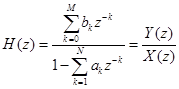(2-2)

由系统函数可以得到系统输入与输出关系的常系数线性差分程为：

(2-3)

IIR滤波器的单位抽样响应h(n)是无限长的，结构上存在着输出信号到输入信号的反馈，在z平面的有限区间(0<︱z︱<∞)有极点存在。

虽然可以直接根据此方程式构建一个高阶IIR滤波器(称为“直接形式”实现)，但量化误差(有限字长)引起的累计误差可能引起不稳定和较大的误差。因此，常常是级联几个具有适当系数的双二阶部分，而不是使用直接形式实现。双二阶部分可以独立缩放，然后级联起来（这种级联和模拟滤波设计思路类似），从而使系数量化和递归累计误差最小。级联双二阶滤波器比相应的直接形式滤波器执行得更慢，但更稳定，并且有限算法误差引起的误差影响降至最小。

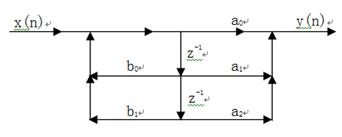
对于二阶的IIR数字滤波器，其传递函数为：

常系数线性差分方程为： (2-4)

(2-5)

其中a_1、a_2、a_3、b_1、b_2、b₃可以由MATLAB工具直接生成。

图2.9二阶结构方框图

IIR属性总结：

1、 反馈(递归)；

2、 可能不稳定；

3、 通常实现为级联双二阶滤波器，而不是直接形式滤波器；

4、 非线性相位；

5、 效率高于FIR滤波器；

6、 抽取输出时无计算优势；

7、 具有类似的模拟滤波器。