原创 基于FPGA的数字滤波设计—IIR设计2

基于FPGA的数字滤波设计—IIR设计2

4.2 系数的量化和归一化

4.2.1系数的量化

表4.1中是用小数来表示系数，如果在不做任何变换的前提来直接拿来计算卷积，那么必须采用单精度浮点数乘法来计算。这样势必给FPGA带来很大的资源消耗。

对系数的量化目的就是为了将小数乘法运算转化为整数乘法运算。量化的方法很简单，对公式4-1两边同时乘以2¹⁴，将系数可能的最大值2量化到2¹⁵，加上符号位整个系数长度刚好为16位，即系数为16bits带符号整型。同时在a2、a3加上符号，将差分方程调整为全加法计算，即，

4-3

得到的量化系数为：

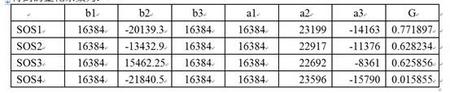
表4.2 量化后的4级SOS系数

将增益调整系数放进下一级SOS系数b1、b2、b3中，即

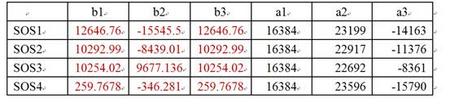表4.3 增益调整后的4级SOS系数

这样做的目的就是为了将低乘法器的使用。计算过程中就可以不再考虑增益调整问题，输入信号X经过四级SOS运算后，幅度没有增强。

4.2.2 系数的归一化

关于a1系数的量化，从差分公式中可以看出，原本a1的值是1，即不需要乘法运算。但是系数量化后a1=2¹⁴=16384那么在计算y(n)输出时带来了除法，而在FPGA中实现2的幂次倍的除法时可以直接利用移位操作来实现，即每个SOS输出结果向右移位14bits，即完成了除法。这个过程就是叫做去归一化。

4.2.3 量化精度对滤波效果的影响

1、量化位数越小，FIR对小信号滤波效果变差（频响、带内增益和带外衰减都存在问题）；

2、量化位数越大，虽然对滤波效果有很大的帮助，但是出现溢出的概率越高；

3、量化中有截断误差。

4.3 IIR的溢出

4.3.1 溢出的产生原因

从数学角度分析差分方程式4-3

假设每一级SOS输入的系数为16bits有符号数，数据为18bits有符号数，则乘法运算结果输出位宽为：

1sign bit+15bits+17bits=33bits，

每累加一次数据位宽增加一位。所以y(n)最大宽度为：

33bits+4bits=37bits。

去归一化之后，每一级SOS输出位宽为：

37bits-14bits=23bits

那么如果将计算位宽调整到23bits是不是就可以保证不会溢出呢？

我们要考虑两个问题，第一个是本级的输出作为下级的输入，如果下级SOS的位宽任然为18bits,那么从数学角度，溢出的情况是肯定会发生的；第二是，本级当前的输出作为下个数据的历史值（即反馈），注意以上位宽在计算时，我们假设数据都是18bits，很显然这是不科学的，因为反馈值y(n-1)和y(n-2)位宽可能已经超出了18bits。

由以上数学角度分析可以得出下面结论：

1、IIR滤波器的溢出是一定存在的；

2、溢出不仅是在IIR接联里某一级SOS产生，可能随着级数的增加而加深（或者说不可控）。

我们再从IIR系数角度分析溢出问题。

IIR每个SOS都可以由一个二阶模拟滤波器与之相对应，即每个SOS都有自己的增益。增益过大那么在本级计算过程中出现溢出的概率越高。所以，我们可以通过调整每级SOS之前的增益调整系数来避免溢出的出现，即，在具有大增益的SOS之前缩小输入值。但这样做带来的结果就是AD精度的丢失。丢失精度带来的结果是，波形存在很多毛刺，且小信号波形失真严重。

在资源有限的情况下，我们必须做此调整来保证不溢出。相对波形失真，我们更不愿意看出溢出。