原创 基于FPGA的数字滤波设计—IIR设计3

基于FPGA的数字滤波设计—IIR设计3

4.3.2调整每级SOS的输入和增益调整系数，将溢出控制在有效范围之内

       先看看表4.1系数在各级SOS处的增益。

图4.1

可以看出第三级SOS增益较大大，此级容易出现溢出现象。分析各级增益对输入输出位宽的影响。

图4.2

由上所述，将增益调整放在下级SOS中计算，所以每一级的SOS增益做了调整。SOS1和SOS2一共提供了大约4倍增益，即16bits左移2位，变成18bits数据，在此，由于我们就是采用18bits位宽计算，所以在两个SOS输出端出现溢出的几率较低。第三级SOS提供了14.2倍的增益，即左移4bits,变成了22bits数据，此时，已经完全溢出。第四级由于衰减系数比较小，所以增益缩小了0.02倍，即22bits右移6bits，又回归到了16bits。

       我们将所有的增益都乘起来得：

整个滤波系统增益为1。

       下面我们就保证系统增益不变的情况下，调整每级的输入位宽和增益调整系数来减低溢出概率。

1、  我们知道由于噪声的存在，16位AD采集到的数据低位都是噪声数据，所以在滤波时，可以丢弃低几位，在这里，我们采用15bits输入。即>>1；

2、  SOS3增益为16倍左右，即会使输入<<4，为了保证输出仍在18bits的动态范围之内，必须将17bits数据>>3后再输入到SOS3中，即>>3；

3、  SOS4本来的增益只有0.02，做了衰减，那么18bits进肯定不会产生溢出。但是我们考虑到SOS4之前我们已经将数据>>4，做了缩小操作，必须在后级中补回来才能保证整个系统的增益为1。我们可以将补偿放在增益调整系数里面，因为前级对信号做了缩小操作所以SOS4之前的增益缩减可以稍微弱点，我们将增益调整系数扩大16倍，即>>4。而曾个SOS4增益变成了0.32，即>>1bits。从数学公式，考虑18bits输入到SOS4中可能会出现溢出，那么我们将数据>>1。即17bits的数据进入SOS4，输出的刚好是16bits数据。

4、  从整个系统角度，数据被我们>>3位（AD缩小1位除外），增益调整系数<<4位，所在整个系统增益放大了1bits。IIR滤波变成了15bits进16bits出的带有增益的滤波器。

5、  数据每>>1一次，就丢失1bits精度，我们一共丢失了5bits的精度，带来的结果就是波形失真。

调整某些级的输入和改进增益调整系数的目的就是为了保证18bits计算无溢出，带来的不良结果是：小信号输入时波形失真严重；噪声变大；频响变差。

       IIR设计过程中的注意点：

1、  MAC的结果不但要给下级SOS，还要作为本级的反馈保存到RAM中，那么在本级反馈回来上，只能去归一化，不能做额外的移位。

2、 

4.4 利用FPGA实现IIR滤波器（32bits计算）

4.4.1 32bits计算精度的选择

       由以上分析可知，18bits计算IIR，在保证不溢出的条件下必须丢失5bits的精度。带来的不良后果是在小信号输入滤波时波形失真，频响失真。所以为了保证无溢出且滤波效果良好，必须采用32bits带符号计算。下面评估18bits和32bits计算下的硬件资源需求。

1.         18bits计算时，每个AD8221芯片需要4个SOS模块，每个SOS需要2个9*9的DSP单元，需要32（24）*8*16bits(18)=1M4K。那么3片AD8221做8阶IIR滤波，总共需要24个DSP和12个M4K。

2.         相同结构的32bits计算IIR资源需求，DSP和M4K都扩大2倍，分别为48和24。

我们知道，2C8器件DSP最大数量为36个，M4K也为36个。显而易见相同结构32bits计算无法在2C8上实现。DSP需求已经大于2C8所能支持的最大数量。所以在结构上面必须做优化。

4.4.2实现结构

       18bits计算时，我们为每路AD8221分配了一个滤波通道，每路滤波通道里面拥有单独的MAC单元。32bits计算时所需的乘法器成为了瓶颈。所以我们优化思想是将三路AD同时送入到一个滤波通道，分时的进入MAC计算。也就是说本来每个MAC只需要算24个模拟通道值，一共有3*4个MAC同时计算，优化后只有1*4个MAC，需要计算72个通道值。所需的DSP个数为16，存储单元的数量不变，2C8器件可以满足要求。

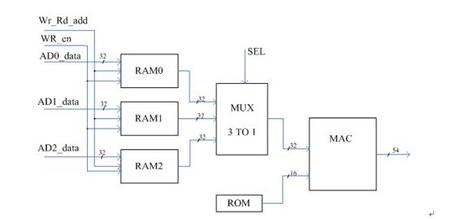
       每一级SOS中的数据路径如图4.3所示，3路AD值存储到3个RAM中，MUX分时将不同的值送到MAC单元中进行乘累加运算。

图4.3 优化后的SOS的数据路径