


在开发板的LCD测试程序中,实现画直线连接两个点的函数如下:
void Glib_Line(int x1,int y1,int x2,int y2,int color)
{
int dx,dy,e;
dx=x2-x1;
dy=y2-y1;
if(dx>=0)
{
if(dy >= 0) // dy>=0
{
if(dx>=dy) // 1/8 octant
{
e=dy-dx/2;
while(x1<=x2)
{
PutPixel(x1,y1,color);
if(e>0){y1+=1;e-=dx;}
x1+=1;
e+=dy;
}
}
else // 2/8 octant
{
e=dx-dy/2;
while(y1<=y2)
{
PutPixel(x1,y1,color);
if(e>0){x1+=1;e-=dy;}
y1+=1;
e+=dx;
}
}
}
else // dy<0
{
dy=-dy; // dy=abs(dy)
if(dx>=dy) // 8/8 octant
{
e=dy-dx/2;
while(x1<=x2)
{
PutPixel(x1,y1,color);
if(e>0){y1-=1;e-=dx;}
x1+=1;
e+=dy;
}
}
else // 7/8 octant
{
e=dx-dy/2;
while(y1>=y2)
{
PutPixel(x1,y1,color);
if(e>0){x1+=1;e-=dy;}
y1-=1;
e+=dx;
}
}
}
}
else //dx<0
{
dx=-dx; //dx=abs(dx)
if(dy >= 0) // dy>=0
{
if(dx>=dy) // 4/8 octant
{
e=dy-dx/2;
while(x1>=x2)
{
PutPixel(x1,y1,color);
if(e>0){y1+=1;e-=dx;}
x1-=1;
e+=dy;
}
}
else // 3/8 octant
{
e=dx-dy/2;
while(y1<=y2)
{
PutPixel(x1,y1,color);
if(e>0){x1-=1;e-=dy;}
y1+=1;
e+=dx;
}
}
}
else // dy<0
{
dy=-dy; // dy=abs(dy)
if(dx>=dy) // 5/8 octant
{
e=dy-dx/2;
while(x1>=x2)
{
PutPixel(x1,y1,color);
if(e>0){y1-=1;e-=dx;}
x1-=1;
e+=dy;
}
}
else // 6/8 octant
{
e=dx-dy/2;
while(y1>=y2)
{
PutPixel(x1,y1,color);
if(e>0){x1-=1;e-=dy;}
y1-=1;
e+=dx;
}
}
}
}
}
只用分析红色部分的代码,即斜率为0和1之间的直线,其他的斜率都可以通过坐标转换得到。这个就是传说中的Bresenham画线算法,以前在《windows游戏编程大师技巧》中看到过,计算机图形学的基础知识。下面找到一篇讲解比较详细的文章,转一下,并对作者表示感谢。
0.算法目的
这个算法是要画一条平滑的直线,这个工作的难点是确定两点之间的那些像素点,使其近可能的靠近手工绘制的直线。
1.基本算法描述
现在我们要在一个光栅格子上画一条直线,我们将直线的斜率严格控制在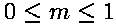 。
。
若我们进一步限定画线的路径:给定一个点后x轴要有一个增量来绘制这条直线的第二个点。这样一来,显而易见若给定点(x,y)后,线上的下一个点就只能在有限的范围之内进行选择了:
它可能是画在(x+1,y),或者画在(x+1,y+1)点。
所以我们在平面上转角为45度的位置进行画线,画线也就是在每个步长上决定这两种可能。
我们以下图为说明,注意这是个栅格的局部放大图,你可以想象是用一个高倍放大镜来看: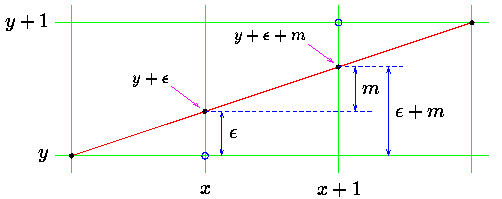
在点(x,y)处画一个点,那么线的路径一般就会在它本应该绘制成什么样子和屏幕的分辨率实际上允许怎样绘制成什么样子这两个问题上进行折衷。通常点 (x,y)的绘制是错误的,所谓“错误”也就是说在事实上,这些数学意义上的点是无法绘制在像素栅格上的。我们设每个实际绘制点的纵坐标y相对应的误差为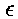 ,那么这些点的数学真值为
,那么这些点的数学真值为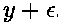 。这个误差应该在-0.5到+0.5之间。
。这个误差应该在-0.5到+0.5之间。
在从x移动到x+1间,我们对其数学上的y纵坐标也增加了斜率大小的值m。那么,若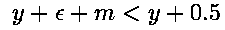 ,我们将选择绘制点(x+1,y)。否则,我们绘制点(x+1,y+1)。其实看看图中的含义,这一步大有四舍五入之感。我们在这一步所作的决定就是在使在屏幕上绘制出来的线和数学上所要画的线之间的总误差最小化。当然前者绘出的图像在局部看来是有些问题的,不过你就忍了吧,这毕竟是机器。
,我们将选择绘制点(x+1,y)。否则,我们绘制点(x+1,y+1)。其实看看图中的含义,这一步大有四舍五入之感。我们在这一步所作的决定就是在使在屏幕上绘制出来的线和数学上所要画的线之间的总误差最小化。当然前者绘出的图像在局部看来是有些问题的,不过你就忍了吧,这毕竟是机器。
这样,新绘制的点带来的误差我们再次记为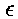 ,这样一来我们就能够在以下的绘制中重复这个过程。新的误差可能采用以下两个可能的值中的一个:若(x+1,y)被选择使用了,那么新的误差就满足
,这样一来我们就能够在以下的绘制中重复这个过程。新的误差可能采用以下两个可能的值中的一个:若(x+1,y)被选择使用了,那么新的误差就满足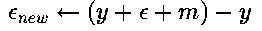 ,反之则新的误差就是
,反之则新的误差就是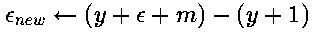 。这个是显而易见的,自己动手画一画就知道了。
。这个是显而易见的,自己动手画一画就知道了。
写成程序描述一下就是:
这依然需要浮点值,我们现在要做的就是将浮点数转化为整数,那么我们试着做如下运算: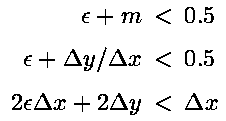
这样一来在这个不等式中出现的变量都成为整数了。
用 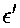 替代
替代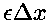 ,我们得到
,我们得到 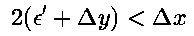 。
。
这就是我们来判断点的绘制所用的不等式了,都是整数运算。
每一步误差的更新也可以写成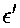 的形式:
的形式: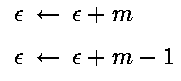
不等式两边都乘以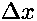 ,则得到
,则得到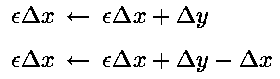
写成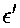 的形式则是:
的形式则是: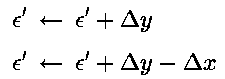
我们重新写一下这个整数版的bresenham算法描述: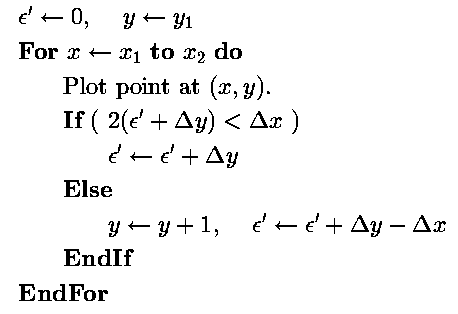
这个描述有一下特点:
都是整数运算当然速度上比较好,而且乘以2这个运算可以用左移运算这个为运算,速度上也不错。
我们用C语言描述的方式再写一遍这个算法:
void linev6(Screen &s,
unsigned x1, unsigned y1,
unsigned x2, unsigned y2,
unsigned char colour )
{
int dx = x2 - x1,
dy = y2 - y1,
y = y1,
eps = 0;
for ( int x = x1; x <= x2; x++ )
{
s.Plot(x,y,colour);
eps += dy;
if ( (eps <<1)>= dx )
{
y++;
eps -= dx;
}
}
}
 /3
/3 
文章评论(0条评论)
登录后参与讨论