原创 传输线_2

2 传输线模型[1.1]

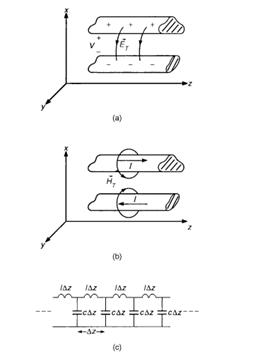
上图a是一条传输线，如果在线的一段施加电压，两条线之间就产生了电势差，从而形成了电场；因为这两条线是分开的，所以可以推断，这两条线之间存储了电荷，这就说明传输线有电容；同样，施加电流，两条导线就会产生磁场，由于磁场存在于这样一个闭合回路中，说明传输线有电感。因此，传输线可以用电容和电感来建模。如果考虑到导线还有电阻，而导体周围的介质还有损耗，传输线的模型还应该加上两项，R和G(电导)。[1.1]

2.1 集总参数建模RLCG模型[4]（双线传输线的情况）

一小段位于电磁场中的传输线可以用下图表示，z是垂直纸面的方向。

如果导体周围的介质具有非零的电导率以至于它是有损耗的，G就表示了这样的损耗。电导率代表了2个导体之间的传导电流，如果周围的介质是无损耗的，G就不存在；在传输线中，G代表了长电缆由于信号导体间的潮湿或绝缘不良而导致的电流泄漏效应的模型[2]。导体不是理想的导体，电位长度的电阻R代表了与导体有关的损耗。如果是无损耗的传输线，R，G都是0。这就是著名的传输线集总参数模型——RLGC模型，我们以后的很多讨论都会用到这个模型。

2.1.1 理想传输线

理想传输线具有3个特征：长度是无限的；线上传播的信号没有畸变；线上传播的信号在行进中不被衰减。即只有L，C，没有R，G。很明显，理想传输线是一个无损耗的传输线，能量只是在L/C之间进行转换。

<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />

2.2 传输线的方程

        要确定传输线上各点的电压和电流，需要用方程来描述。描述有两种方法，一种是在时域，另一种是在频域。

2.2.1 理想传输线的时域方程[1.1]

        由于已经知道了理想传输线的模型，我们就可以对这段模型直接列写方程。由于这一小段微元可以看成集总参数模型，因此，基尔霍夫定律仍然适用。（应用RLGC模型时注意集总参数模型成立的条件）

下面我们来为这个模型建立方程

从而得到两个方程：

将4.2a对z求偏导数，4.2b对t求偏导数，得到：

这两组方程基本上是相同的。4.2是一阶的方程，但是是耦合的；4.3是二阶的方程，但是是非耦合的。

然后，解这个偏微分方程组，得到：

注：这个方程组的解法可以在很多电磁场的书里面找到。

V是电磁波在导线上的传播速度。Zc叫做特性阻抗。其中，

而方程组的解中，V⁺，叫做前向行波，V^-，叫做后向行波，分别表示向前(向远端)和向后(向源端)传播的波。我们把在负载端V⁺ V^-比值叫做反射系数，很明显，这是电压的反射系数。电流也有，但不常用。

以上就是传输线方程的时域解。原则上，从这个方程，我们就可以得到传输线上任何一点，任何时刻的电压和电流。