加法器(Adder) 是非常重要的,它不仅是其它复杂算术运算的基础,也是 CPU 中 ALU 的核心部件(全加器)。在数字计算机中,两个二进制数之间的算术逻辑运算(加、减、乘、除),基本上都是化成若干步加法操作进行的。因此,学好数字电路,数字 IC 设计的入门,从学好加法器开始。
加法器分为 半加器(Half Adder) 和 全加器(Full Adder) 。全加器和半加器相比,只是 多了一个来自低位的单比特信号相加的进位输入 ,
全加器就是 3 位相加,半加器就是 2 位相加。例如,我们在做加法运算的时候,总是需要进行低位进位的判断,接着进行下一位的计算,这就是全加器的由来。此外,下文的 RTL 代码中的 {} 符号表示的是 “拼接位” ,即先计算 a 与 b 的值,当 a 与 b 分别为 “0” 和 “1” 时,它们之和为 1,那么就是{01},对应 cout 和 sum ;当 a 与 b 为 “1” 和 “1” 时,它们之和为 2,那么就是转换为二进制就是{10},同样对应 cout 和 sum 等等。
说太多,都不如底层硬件代码和设计电路看一看、学一学!!!
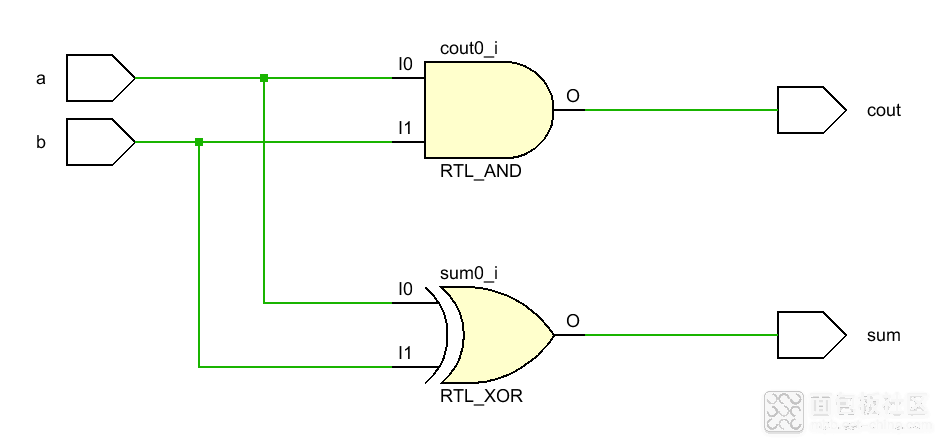
可基于多种方式描述的半加器的 Verilog 代码和 RTL 电路
Plaintext module Half_Adder( input wire a, // 加数 input wire b, // 加数 output reg sum, // 和 output reg cout // 进位输出 ); // 行为描述 always @(a or b) begin sum = a ^ b; // 实践证明,这里 <= 和 = 的结果都一样;都是纯粹的组合逻辑; cout = a & b; end // 数据流描述 // assign sum = a ^ b; // assign cout = a & b; // 门级描述 // and(cout,a,b); // xor(sum,a,b); endmodule
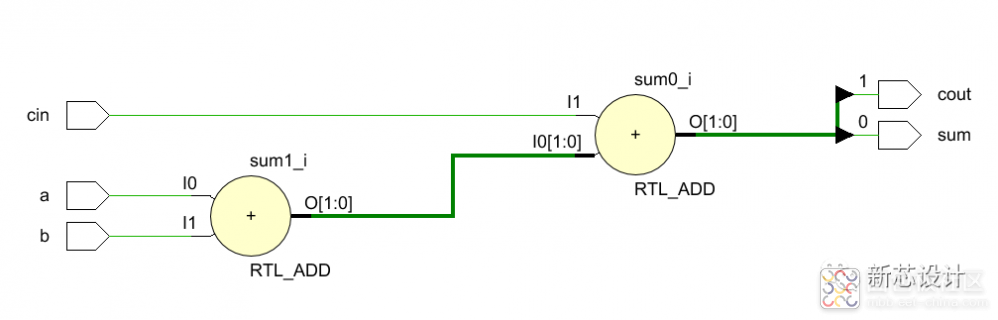
可基于多种方式描述的全加器的 Verilog 代码和 RTL 电路
Plaintext module Full_Adder( input wire a, // 加数 input wire b, // 加数 input wire cin,// 进位输入 output reg sum, // 和 output reg cout // 进位输出 ); // 行为描述 always @(a or b or cin) begin {cout,sum} <= a + b + cin; end // 行为描述 // always @(a or b or cin) begin // sum = a ^ b ^ cin; // 实践证明,这里 <= 和 = 的结果都一样;都是纯粹的组合逻辑; // cout = a & b | b & cin | a & cin; // end // 数据流描述 // assign {cout,sum} = a + b + cin; endmodule



 /4
/4 
文章评论(0条评论)
登录后参与讨论