原创 【博客大赛】在FPGA中利用LFSR实现PRBS

在FPGA中利用LFSR实现PRBS

概述

         LFSR（Linear Feedback Shift-Register），即线性反馈移位寄存器，可以用于创建Pseudo-Random Binary Sequence （PRBS），即伪随机序列，的一种逻辑电路。一个LFSR电路有一系列M寄存器和决定序列转换状态的反馈抽头组成。反馈抽头由模-2多项式描述。对于一个M级LFSR来说，最多可以有2^m个状态，全“0”状态不会转入其他状态，所以LFSR的最长周期是2^m-1。而PRBS是LFSR的二进制输出。

         LFRS和PRBS在数字系统被广泛使用。在SONET应用中PRBS7需要被用于数据扩展（Data Spreading）（每个数据位被一个PRBS位调制），而在CDMA无线通信里，PRBS序列被用于产生扩频数据（每个数据位被一个PRBS位调制）以及同步（基站发送已知的PRBS码）。在高速串行系统，PRBS需要被用于BER（bit-error-rate）测试（这个可以在ALTERA带GXB的器件中经常看到此应用）。在数据处理中，PRBS有时候还会用于白噪声的产生，例如，作为数字噪声源。

拓扑结构

图1显示了LFSR两种通用的拓扑结构，即斐波那契（Fibonacci）和伽罗瓦（Galois）。这两种拓扑结构和移项操作有关。图1显示了序列的移项方式，图1-a是Fibonacci，改变移项以及求和节点方向后就可以转换成图1-b所示的Galois拓扑。图1-c通过转换，得到和图1-a一样移项方向的Galois拓扑结构。

图1所示的“求和节点”其实就是一个模-2加法器，可以用典型的XOR门来实现。可以用XNOR门（即对求和取反）来替代XOR来实现求和节点。理由是基于XOR门的LFSR的无效状态时全零状态；由于事实上如果移位寄存器加载零值，模-2求和结果还是为零，这样LFSR状态就永远不会改变。而基于XNOR门的LFSR序列的无效状态是上述基于XOR的无效状态的补码（取反），所以这时候无效状态为全1。

图1显示了Fibonacci和Galois两种拓扑结构之间非常有趣的差异，即Fibonacci结构通过求和节点时（可能需要宽输入异或门）有一个潜在的长组合路径，而Galois形式的每个求和节点都是寄存器输出。这意味着，Galois更适合在FPGA中实现。然而，LFSR原始多项式一般只有2个、4个或者6个反馈抽头，这些反馈抽头用一个或者很少几个LE即可实现，所以两种结构并无明显比对方更容易实现优点。对于并行输出的PRBS，两种结构电路都是对多输入求和并寄存器输出，使得电路变成一个更复杂的系统，所以再次表明，这两种结构彼此之间并没比对方更优特点。

图1：LFSR两种通用拓扑结构

多项式符号

         LFSR反馈抽头由模-2多项式描述，反馈点由特征多项式决定。原始多项式（Primitive Polynomials）产生最长序列（即m序列），这时候特征多项式等于原始多项式。有多种形式可以表示多项式，比如抽头形式、功能形式以及二进制形式（也可以表现为十进制或者十六进制）。图1显示的两种拓扑结构中，Xⁿ表示了多项式反馈抽头。图2分别用这三种形式显示了一个7-bit LFSR（PRBS7）序列，其抽头为[7，6]，功能多项式为X⁷+X⁶+1，二进制形式为1100_0001b = C1h = 193。图2所示的拓扑结构还有一个镜像多项式，即X⁷+X¹+1，1000_0011b = 83h = 131。

         在使用多项式和对应硬件实现LFSR和PRBS时有许多的歧义使用，而且歧义产生源头有多处。你比如在图1移位方向上定义有抽头索引，在图2中，有相关于抽头的索引定义的移位寄存器索引。如果任何上述索引改变（比如取反）那么一个不同的LFSR就被实现了。另外，事实上LFSR存在的镜像多项式对（其实就是反向序列）也是产生歧义的源头之一。

图2：多项式X⁷+X⁶+1的PRBS7 LFSR拓扑结构

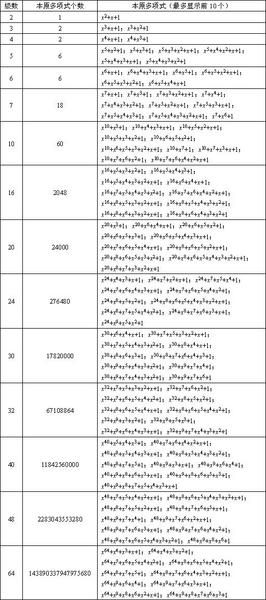
图3：某些级数下本原多项式个数以及前10个本原多项式的对照表

一个实例

以48级本原多项式x⁴⁸+x⁹+x⁸+x⁶+1为例，其周期为281474976710655（约256Tbits），假如以1Mbps的速率发送，发送一个完整周期的时间为约9年。其移位寄存器表示形式为BIN = B9 XOR B8 XOR B6 XOR B0。可以在FPGA中用如图4所示方法实现。

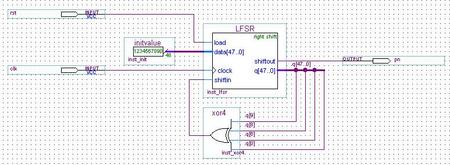
图4：48级PRBS在FPGA中的一个实现

移位寄存器在复位时，从data[47..0]载入常数1234567890作为种子。种子不同时生成的序列有很大差别。两个具有相同种子相同结构的PRBS发生器产生的序列完全一样。