二阶系统的直觉分析

实际上，我们很少在乎电路系统的暂态过程，因为它比较复杂，一段有限的时间后就会消失。超过95%的情况都只关心稳态响应。但在很多情况下暂态过程也比较重要，比如高速数字电路中。所以，本文简单整理一下二阶系统的暂态和稳态响应，以加深记忆。

这是需要考虑RLC暂态响应的一个例子，数字电路中如SPI信号线上添加电阻也是为了避免欠阻尼。

一、二阶系统

二阶系统即有两个独立的储能元件，可以是一个电感和一个电容，或者两个独立电容（可以合并成一个电容的不算），或两个独立电感（可以合并成一个电感的不算）等。当然还包括电源和电阻。这就构成了所谓的二阶系统。

只有一个电感和一个电容组成的二阶系统才有可能震荡，两个独立电容或电感构成的二阶系统是无条件稳定的。

常见的呈现震荡性质的物理系统几乎都是二阶系统，如钟摆，可能发生震荡的运放电路等，很常见。它与一阶系统的暂态过程完全不同。

二阶电路最终都可以化简成特征方程的标准形式（S^2+2aS+W0^2=0），知道了它就基本知道了关于它的一切。几个关键参数的计算公式参见表1，物理意义参见表2。

表1 二阶系统的几个关键参数-1

表2 二阶系统的几个关键参数-2

关键参数	物理意义
衰减因子a（rad/s）	1、a与W0的相对大小可以很方便的分为三种情况，a小于W0时为欠阻尼，大于时为过阻尼，等于时为临界阻尼； 2、W0为系统中无阻尼时正弦衰减震荡的频率；
无阻尼自然频率W0（rad/s）
有阻尼自然频率Wd（rad/s）	Wd为系统中有阻尼时正弦衰减震荡的频率；
频率因数Q	电路中任何支路变量的暂态响应都将是一个衰减的正弦，它的幅值在震荡的Q个周期内衰减至4%；当然，Q还有别的物理意义。

我们分析的电路参见图1。这是经过调整，成了一个欠阻尼电路，临界阻尼也类似，但过阻尼就不会震荡了。关键参数计算如图2。

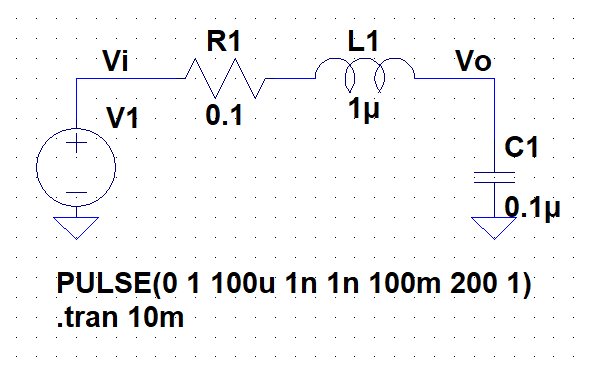
图1 二阶RLC电路

我们可以跟仿真结果对一下，看是否吻合。对比图2、3和4，可以看到计算与仿真结果基本是吻合的。但没有计算公式可以计算出震荡最大的幅值（最大不会超过2倍的输入电压）。

图2 根据第二节相关公式计算出关键参数数值

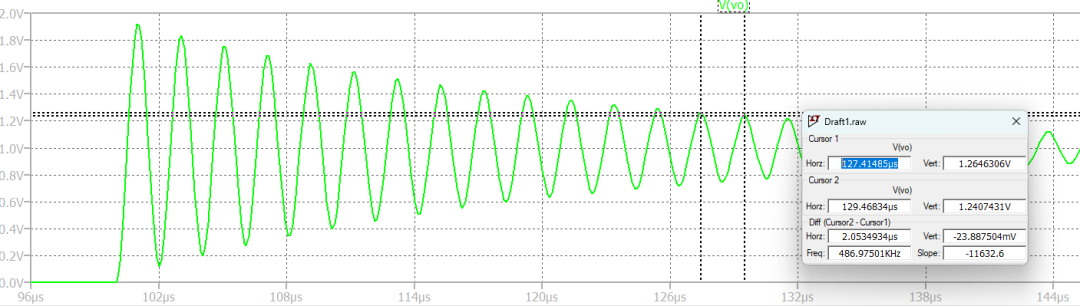
图3 震荡频率约2us，图2的Wd计算结果基本吻合

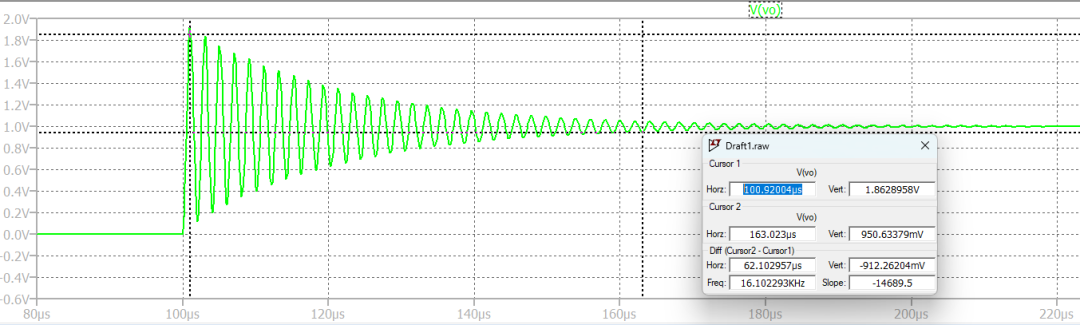
图4 Q个震荡周期大概62us后，暂态响应稳定在了950mV，与图2计算结果基本吻合

我们再从稳态角度看下图2电路的仿真结果，可以看到，它的震荡频率为502Khz，与图2计算得到的Wd是一样的。这说明阻抗法和微分方程最终得到了一样的结果。

所以我们只要学会并用好阻抗法就足够了。

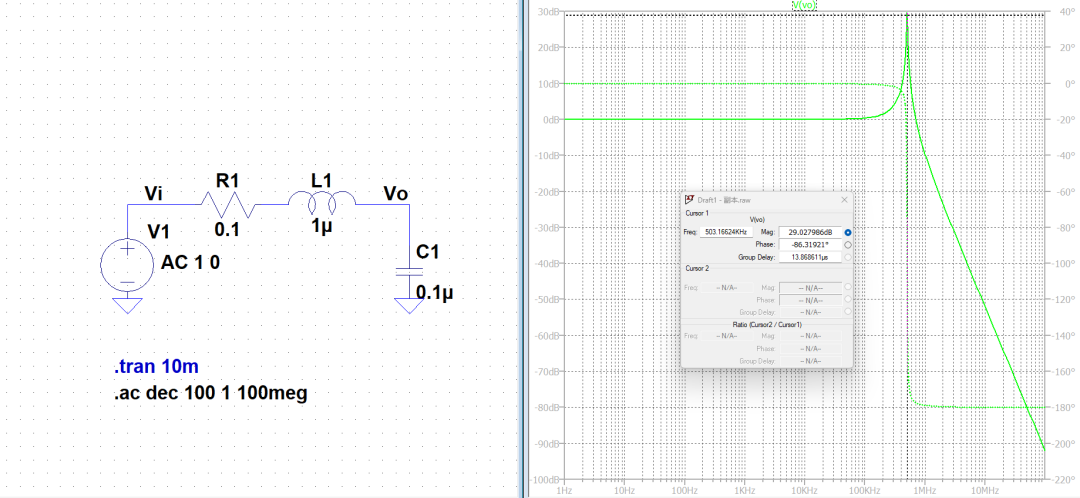
图5 二阶系统的稳态分析-频域响应