-
1.1 成正比
-
1.2 成反比
-
2.1 相关性定义
-
2.2 相关性分类
-
3.1 区分成正比和正相关
-
3.2 区分线性关系和非线性关系
-
3.3 线性模型和非线性模型的区别
一、成比例关系
成比例关系分为成正比和成反比。成正比和成反比都是指两种变量以某种确定性的关系相互关联,一种量变化,另一种量也随之变化。
1.1 成正比
两种变量的比值一定,称这两种量成正比,用数学语言表示为或,其中为常量且。
注意:形如和都是成正比的关系!也就是说,两种变量的比值可以为正、可以为负,只要比值一定,就一定是成正比关系。
1.2 成反比
两种变量的乘积一定,称这两种量成反比例,用数学语言表示为:或,其中为常量且。
注意:形如和都是成反比的关系!也就是说,两种变量的乘积可以为正、可以为负,只要乘积一定,就一定是成反比关系。
二、相关性关系
2.1 相关性定义
相关关系是客观现象存在的一种 非确定 的相互依存关系,即自变量的每一个取值,因变量由于受随机因素影响,与其所对应的数值是非确定性的。相关关系中的自变量和因变量没有严格的区别,可以互换。 因果关系一定是相关关系,反之不一定成立。
相关的概念常见于概率统计学,相关性的大小可以用相关系数描述,常用的相关系数是皮尔逊Pearson相关系数。随机变量的相关性本质是由协方差决定的。 当时,X和Y正相关;当时,X和Y负相关;当时,X和Y不相关。
2.2 相关性分类
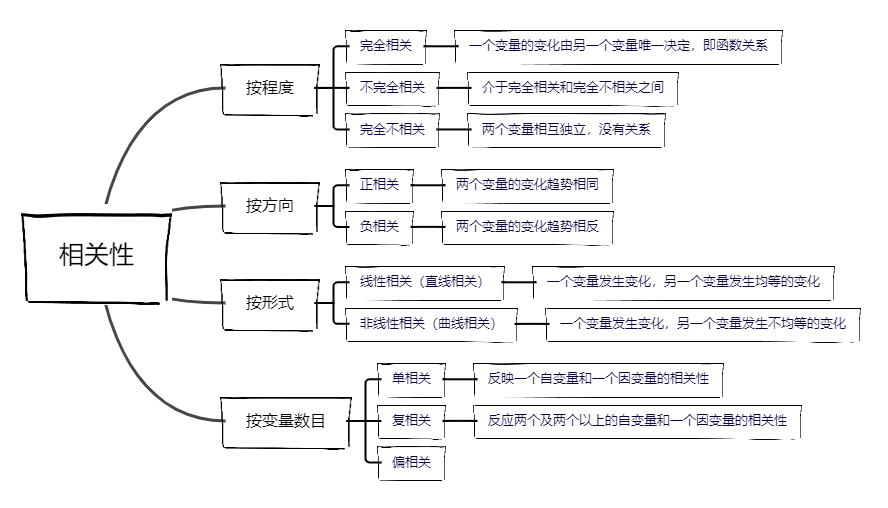
三、区分几组关系
3.1 区分成正比和正相关
正相关是一种概念,是统计学上通过大量的数据统计出来的变量关系:一个变量增大,另一个变量也增大。正相关可以是线性的,也可以是非线性的。比如常见的正相关函数有:, , , 等。而正比表现为直线,有具体的线性关系(可以用确切的数学公式表示出来)。
成正比是相关关系中的特殊情况,如下图,完全正线性相关和完全负线性相关都是成正比关系。成正比和正相关没有必然联系,成正比的变量不一定正相关,只有比例系数时,两个变量才是正相关;反之,正相关的变量不一定成正比,只有当时,且,两个变量才是成正比。(牢记并区分定义!)
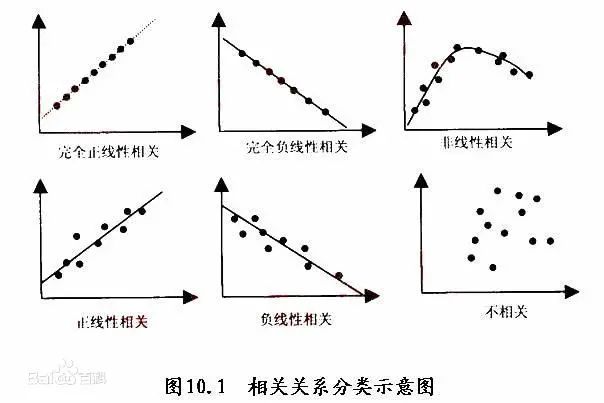
3.2 区分线性关系和非线性关系
线性关系是指自变量和因变量之间是按比例、成直线的关系,在图形上表现为规则、光滑、均等的运动,在数学上理解是一阶导数为常数的函数。线性方程又称一次方程,指自变量都是一次的方程,一般形式为:。
非线性关系是指自变量和因变量之间不是按比例、不成直线的关系,代表不规则地运动,一阶导数不为常数。非线性方程对比于线性方程,是含有高次项的方程,是一阶导数不为常数的方程组。线性关系是互不相干的独立关系,而非线性关系是相互作用的联系关系。
3.3 线性模型和非线性模型的区别
从数学上理解,因变量函数对自变量的依赖关系是否是线性,模型方程是否可以用一次线性方程来表示,或者因变量对所有自变量的偏导数是否均是常数;
从样本分布理解,量与量之间是否按照比例成直线关系,或者是否可以用直线将样本划分开;
要注意的是:线性模型可以用曲线拟合样本,但分类的决策边界一定是直线,例如logistics模型。区分是否是线性模型,主要看决策边界是否是直线。


 0
0










