SPC—统计过程控制,要解决两个问题:1.过程稳定不稳定?2.过程能力够不够?稳不稳定的问题,依靠“控制图”来解决;能力够不够的问题,依靠“过程能力”来解决。

图一休·哈特
它是将正态分布图逆时针旋转90°得到的,取±3σ(标准差)作为控制限。控制图由三部分组成:1)数据点;2)中心线centerline=CL;3)控制限UCL/LCL=X± 3σ,如图二所示。
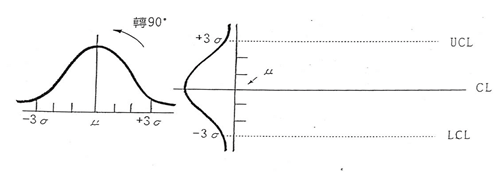
图二控制图的组成
控制图的理论依据有两个:1.质量波动原理;2.小概率事件。因此控制图有一定的抽样风险(错报或漏报),降低风险可借助8条判异原则,如图三所示。这8条判异原则可借助1、(2、3) 、(4、5) 、 6、8 、9、14 、15这些数字来方便记忆。
|
|
典型特殊原因识别准则的汇总 |
|
1 |
一个点远离中心线超过3个标准差 |
|
2 |
连续9点位于中心线一侧 |
|
3 |
连续6点上升或下降 |
|
4 |
连续14点交替上下变化 |
|
5 |
2/3的点距中心线的距离超过2个标准差(同一侧) |
|
6 |
4/5的点距中心线的距离超过1个标准差(同一侧) |
|
7 |
连续15个点排列在中心线1个标准差范围内(任一侧) |
|
8 |
连续8个点距中心线的距离大于1个标准差(任一侧) |
图三 8条判异原则
控制图跟数据类型有关,不同的数据类型对应不同的控制图,其对应关系如图四所示。
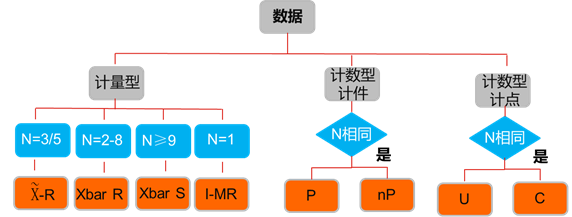
图四数据类型与控制图对应关系
控制图中最常用是均值—极差图,即Xbar—R控制图,其中心线和控制限的计算公式如下:

图五Xbar—R图中心线和控制限的计算公式
过程能力指数—Cpk,是指过程的加工质量满足技术标准的能力,计算公式Cpk=min{(USL-Xbar)/3σ,(Xbar-LSL)/3σ}。他的应用条件是过程稳定且数据是正态分布的质量特性。
过程能力指数Cpk值的评价参考标准如下:
|
Cpk值的范围 |
过程能力的评价参考 |
|
Cpk≥1.67 |
过程能力满足要求,可简化质量检验工作 |
|
1.33 ≤ Cpk < 1.67 |
过程能力尚可,但需要改善 |
|
1.00≤ Cpk< 1.33 |
过程能力不足 |
在中心值无偏移的情况下,Cpk值与不良PPM对应关系如下:
|
Cpk值 |
不良PPM |
|
1.0 |
2700 |
|
1.33 |
63 |
|
1.67 |
0.57 |
步骤1:确定质量指标,收集数据。一般取25个子组,子组大小为5。如对5A管梁左段孔径5.5±0.1mm尺寸进行连续抽样,并记录在预先设计好的表格中,数据如下:
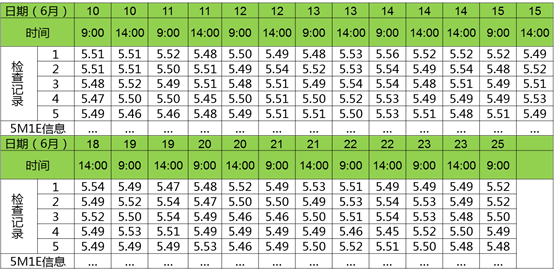
步骤2:计算观测值的总均值X=5.50,平均极差R=0.05。
步骤3:计算R图控制线、X图控制线,并作图。
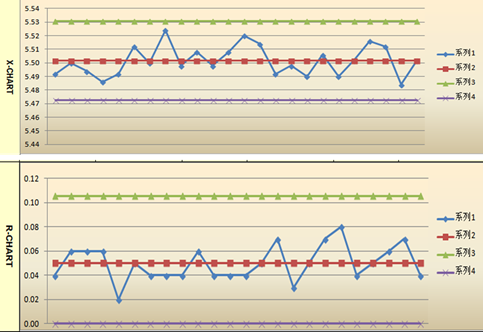
步骤4:依据判异原则判定,其生产过程处于稳定受控状态。
步骤5:计算过程能力指数Cpk=1.57,能力尚可,满足技术要求。
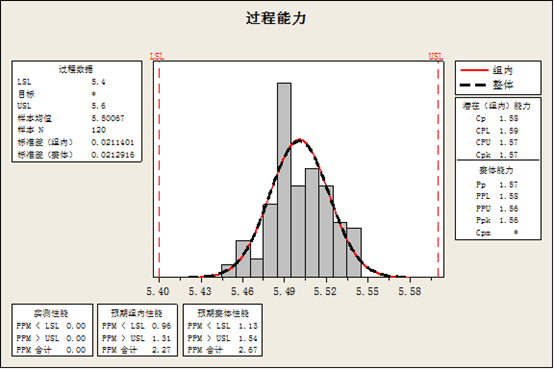
步骤6:延长X-R控制图的控制线,作控制用控制图,进行日常管理。


 0
0








