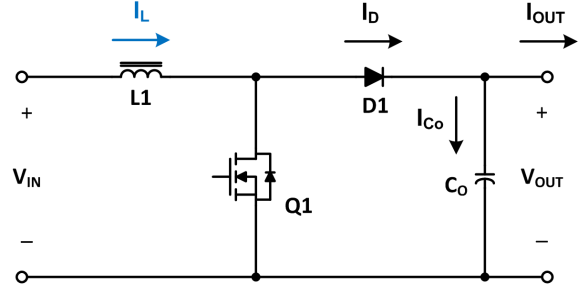
导通模式
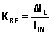 (1) , 其中
(1) , 其中 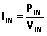 (2)
(2)在连续导通模式 (CCM) 中,正常开关周期内,瞬时电感电流不会达到零 (图1)。因此,当 ΔIL 小于 IIN 的2倍或 KRF <2时,CCM 维持不变。MOSFET 或二极管必须以 CCM 导通。这种模式通常适用于中等功率和高功率转换器,以最大限度地降低元件中电流的峰值和均方根值。当 KRF > 2 且每个开关周期内都允许电感电流衰减到零时,会出现非连续导通模式 (DCM) (图2)。直到下一个开关周期开始前,电感电流保持为零,二极管和 MOSFET 都不导通。这一非导通时间即称为 tidle。DCM 可提供更低的电感值,并避免输出二极管反向恢复损耗。
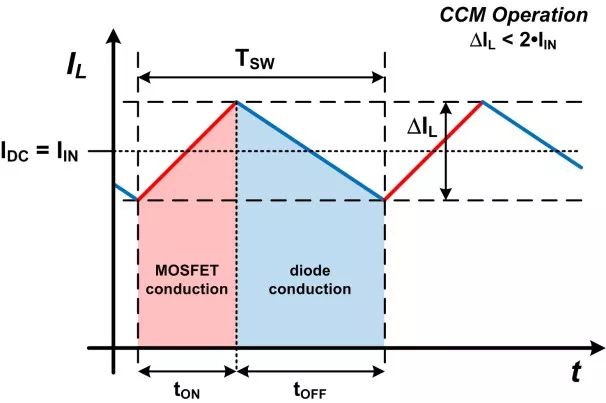
图1 – CCM 运行
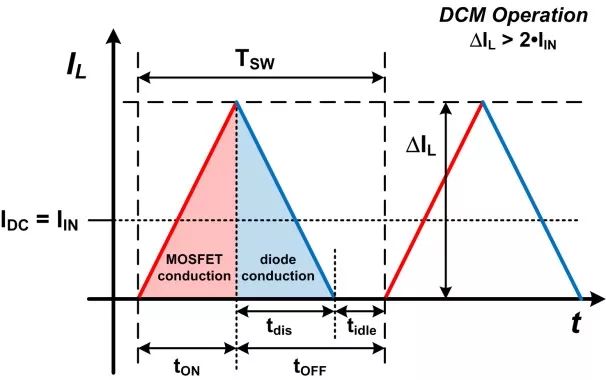
图2 – DCM 运行
当 KRF = 2 时,转换器被认为处于临界导通模式 (CrCM) 或边界导通模式 (BCM)。在这种模式下,电感电流在周期结束时达到零,正如 MOSFET 会在下一周期开始时导通。对于需要一定范围输入电压 ( VIN)的应用,固定频率转换器通常在设计上能够在最大负载的情况下在指定 VIN 范围内,以所需要的单一导通模式 (CCM 或 DCM) 工作。随着负载减少,CCM 转换器最终将进入 DCM 工作。在给定 VIN 下,使导通模式发生变化的负载就是临界负载(ICRIT)。在给定 VIN 下,引发 CrCM / BCM 的电感值被称为临界电感(LCRIT),通常发生于最大负载的情况下。
纹波电流与 VIN
根据
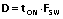 (3)、
(3)、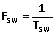 (4) 和
(4) 和 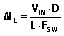 (5),
(5),并通过 CCM 或 CrCM 的电感伏秒平衡
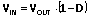 (6),
(6),则
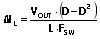 (7).
(7).将导数设置为零,
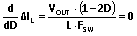 (8)
(8)我们就能得出
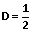 (9).
(9).
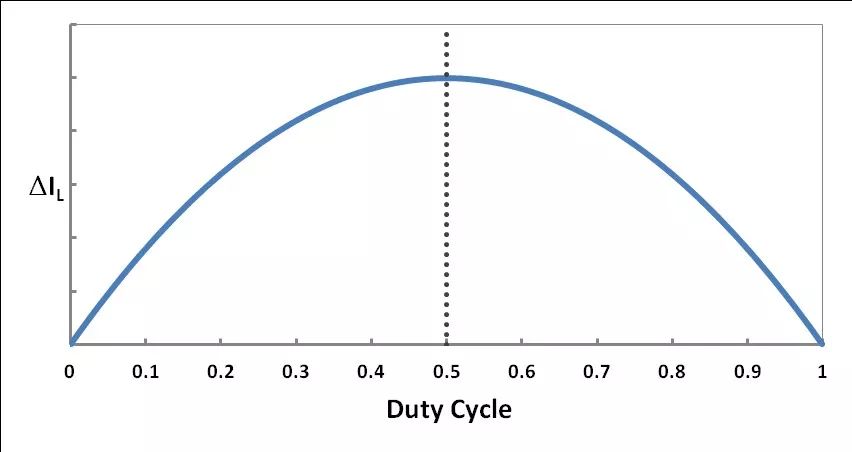
图3 – CCM 中的电感纹波电流
CCM 工作
假设 η = 100%, 则
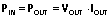 (10),
(10), 然后将(2)、(6)、(7) 和 (10) 代入(1) ,得出:
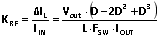 (11)
(11) 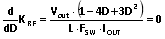 (12).
(12). 对 D 求解,可得
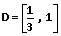 (13).
(13).D = 1 这一伪解可被忽略,因为它在稳态下实际上是不可能出现的 (对于升压转换器,占空比必须小于1.0)。因此,当 D =⅓ 或 VIN = ⅔VOUT 时的纹波因数 KRF 最高,如图4所示。使用同样的方法还能得出在同一点的最大值 LMIN、LCRIT 和 ICRIT。
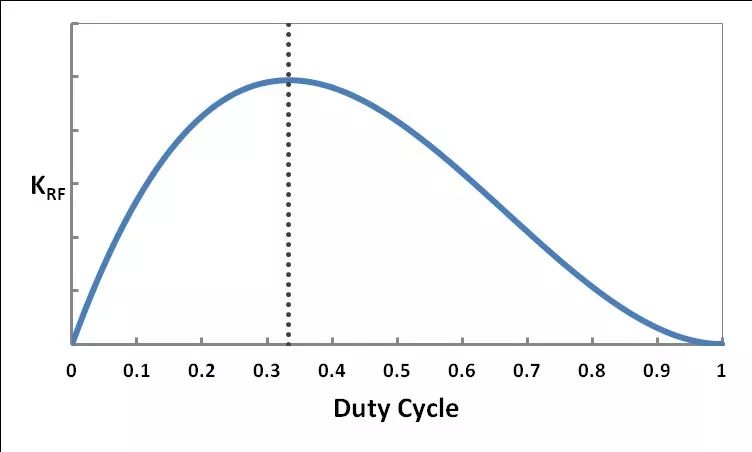
图4 – 当 D =⅓ 时 CCM 纹波系数 KRF 最高值
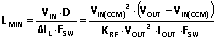 (14),其中 VIN(CCM) 为最接近⅔VOUT 的实际工作 VIN。
(14),其中 VIN(CCM) 为最接近⅔VOUT 的实际工作 VIN。 对于临界电感与 VIN 和 IOUT 的变化,KRF = 2,可得出
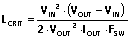 (15).
(15).在给定 VIN 和 L 值的条件下,当 KRF = 2时,即出现临界负载 (ICRIT):
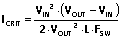 (16)
(16)DCM 工作
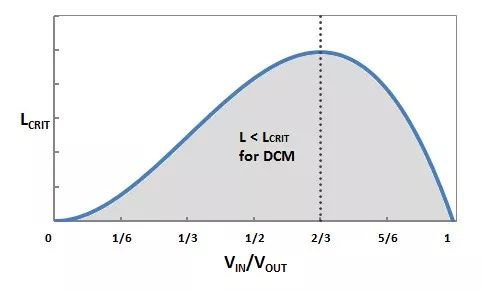
图5 – LCRIT 与标准化 VIN 的变化
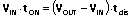 (17),其中
(17),其中 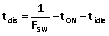 (18)
(18)可得出
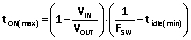 (19).
(19).平均 (直流) 电感电流等于转换器直流输入电流,通过重新排列 (17),可得出 tdis 相对于 tON 的函数。简单起见,我们将再次假设 PIN = POUT。
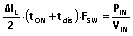 (20) ,其中
(20) ,其中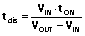 (21).
(21).将方程 (3)、(5)、(10)、(19) 和 (21) 代入 (20),求得 VIN (DCM) 下的 L
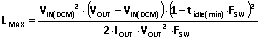 (22).
(22).LMAX 遵循类似于 LCRIT 的曲线,且同在 VIN = ⅔VOUT 时达到峰值。为确保最小 tidle,要计算与此工作点相反的实际工作输入电压 (VIN (DCM)) 下的最低 LMAX 值。根据应用的实际输入电压范围,VIN(DCM) 将等于最小或最大工作 VIN。若整体输入电压范围高于或低于 ⅔ VOUT(含⅔ VOUT),则 VIN(DCM) 是距 ⅔ VOUT 最远的输入电压。若输入电压范围覆盖到了 ⅔ VOUT,则在最小和最大 VIN 处计算电感,并选择较低 (最差情况下) 的电感值。或者,以图表方式对 VIN 进行评估,以确定最差情况。
输入电压模式边界
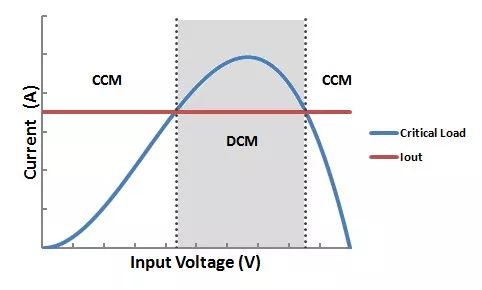
图6 – 输入电压模式边界
要想以代数方式呈现 VIN 的模式边界,首先将临界负载的表达式设置为等于相关输出电流,以查找交点: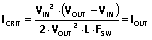 (23).
(23).这可以重写为一个三次方程,KCM 可通过常数计算得出
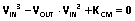 (24) 其中
(24) 其中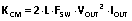 (25).
(25).这里,三次方程通式 x3 + ax2 + bx + c = 0 的三个解可通过三次方程的三角函数解法得出 [1] [2]。在此情况下,x1 项的“b”系数为零。我们将解定义为矢量 VMB。
我们知道
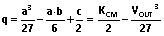 (26)、
(26)、 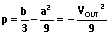 (27)、 以及
(27)、 以及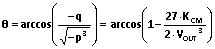 (28),
(28),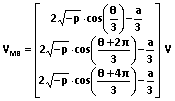
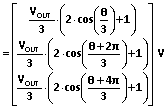 (29).
(29).由于升压转换器的物理限制,任何 VMB ≤ 0或VMB > VOUT 的解均可忽略。两个正解均为模式边界处 VIN 的有效值。
模式边界 – 设计示例
VOUT = 12 V
IOUT = 1 A
L = 6 μH
FSW = 100 kHz
首先,通过 (25) 和 (28) 计算得出 KCM 和 θ:
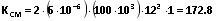
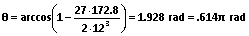 .
.将 VOUT 和计算所得的 θ 值代入 (29),得出模式边界处的 VIN 值:
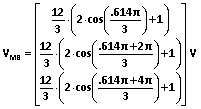
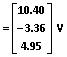 .
.忽略伪解 (-3.36 V),我们在 4.95 V 和 10.40 V 得到两个输入电压模式边界。这些计算值与图7所示的交点相符。
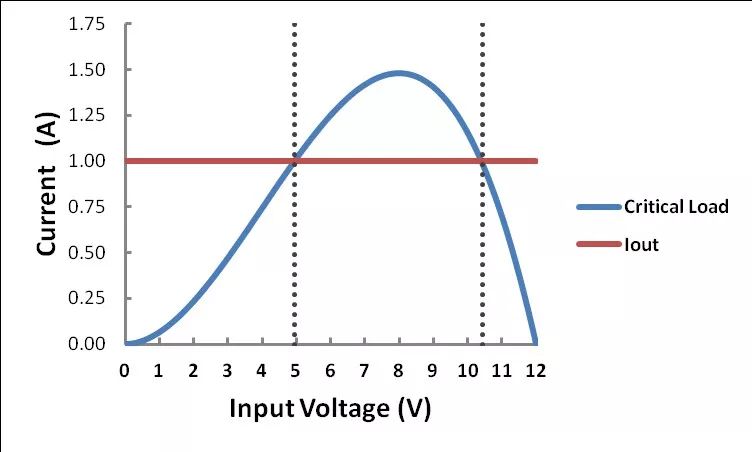
图7 – 计算得出的模式边界
结论
参考文献
[2] I. J. Zucker, "The cubic equation - a new look at the irreducible case," The Mathematical Gazette, vol. 92, no. 524, pp. 264-268, July 2008.


 0
0









