最近找到一本很好看的控制论主题的书，名字叫《The Fundamentals of control theory》。还很薄，只有一百五十多页。学习这本书真是一举两得，既能够学习一些控制论，还能够练习英语。

本文主要是我在学完线性时不变系统那节后，为了加深记忆和理解所记录的笔记。如标题所示，主要内容是线性时不变系统（LTI，linear time-invariant system）的三个性质。

在具体展开前，先介绍下背景吧。线性时不变系统是传递函数的第一小节，只有符合线性时不变性质的系统才能用传递函数的。那为啥非得用传递函数描述系统呢？因为简单。我们可以用任何方式描述系统的，如文字啦、图片啦还有方程；用方程的也有不少选择，如微分方程等。如果我们的目的是为了设计一个需要的工程系统，那么只用文字图片进行系统行为描述是完全行不通的，因为没有可操作性。所以方程成了主要系统行为描述工具，而微分方程求解是非常复杂的，所以为了简化就有了传递函数和状态空间表达式两种方式，一般称前者为古典控制论，后者为现代控制论。在原书中，作者对此做了举例解释，解释了为什么用文字及图片主要描述系统对于设计系统没有用处、用微分方程描述系统是如何的复杂。而传递函数是全书的第二章，第一章比较抽象，回头会再整理下以加深记忆。

如果我们描述系统行为时，把该系统当作线性时不变系统描述时，将大大简化工作。这样，你可以用的数学运算就只有六种了！见图1.如何你只用这六种运算的任意组合去描述系统的话，那么你将能够确定，输入的变化将会导致输出的怎样变化。这是因为线性时不变系统具有三个性质，齐次性、叠加性和时不变特性。正是这些性质让输出的行为变得可预测。下面分别介绍这三种性质。

图1

任何线性系统都具有齐次性和叠加性。我理解着，齐次性就是输入乘以一个常数后，输出就会乘以同样的常数。叠加行是两组输入和输出，如果两个输入相加，那么就等于每个输入对应的输出分别相加。这么描述可能太不准确了，详细解释见图2，3。

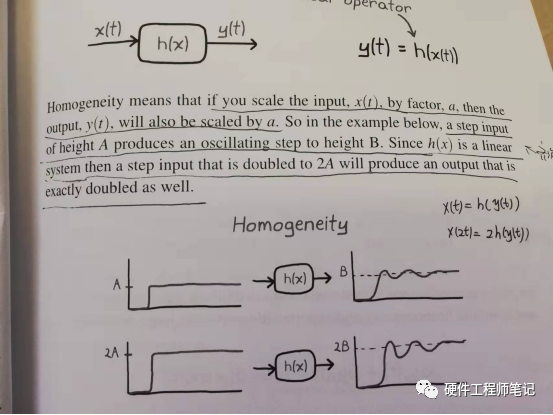
图2

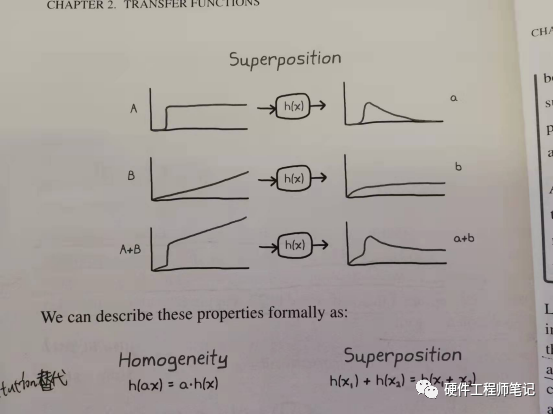
图3

如果一种系统具有这两种性质就可以认为它是线性的了。像电路里面的电阻电容电感就都是线性元件，因为描述他们电流电压关系的方程具有这两种性质。

作者特别提到，线性方程和线性系统是两回事。描述线性系统时，它是两个矢量即输入和输出的映射，映射关系满足齐次性和叠加性时，我们称其为线性系统。而线性方程是一种代数描述，这里每项都是变量的一次方乘以一个常数。见图4，直线方程不符合齐次性的一个例子。

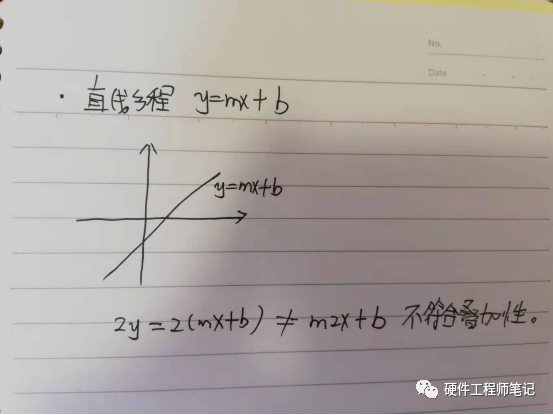
图4（不符合齐次性，图中有误）

另一部分是时不变特性，指的是不管什么时间，系统发生的行为都是一样的。有时候也指的是不管系统在任何地方、任何行为发生的行为都是一样的。见图5

图5

以上就是线性系统的三个性质了，齐次性、叠加性和时不变。可见线性时不变系统的限制是非常严重的，因为真实物理系统中同时满足这三种性质几乎是没有的。见图6，弹簧只在一定长度伸缩是基本满足线性系统的，超过这个长度伸缩就不再是线性系统了。

图6

那如果真实物理系统基本都无法满足线性系统的三条性质，那我们为什么学习它呢？它重要在哪里、又对理解传递函数有啥用处呢？它的重要性正如物理学家费曼所说，”linear system is important because we can solve them”.我们有很多数学工具可以求解线性系统，如果是非线性系统，就只能求解一些最简单的了。即使真实物理系统不符合LTI要求的条件，我们也有方法让它近似成为线性系统，如模拟电路中的小信号就是这样，信号比较小时，在二极管等这类非线性元件偏置点附近工作，我们是可以把它看作线性系统的，见图7。即在这个区域内，它是可以非常近似成线性系统的。还有一种近似成线性系统的方法是线性化，本书后面章节会讲，比如最小二乘法应该算吧。至于它为什么对于理解传递函数有帮助，即定义传递函数为什么都会要求系统是线性的，后面的脉冲函数章节会有解释。

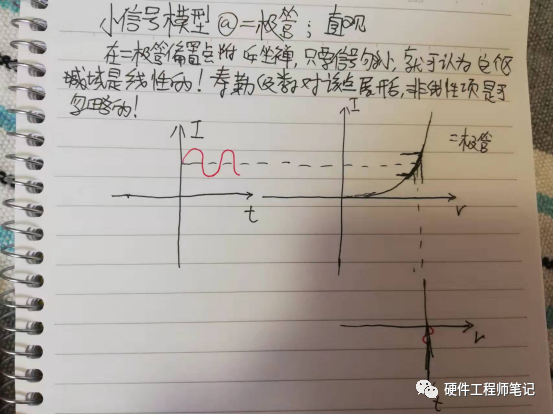
图7