一. FOC之使用Cordic算法求解sin/cos

在进行坐标变换的时候，需要计算角度的正余弦值，而在FPGA中是不能直接进行求解的，需要采用其它的方式进行求解。最常使用的方法有如下两种:

1. 基于ROM的查找表方式:  首先在PC上使用python等高级语言将一个周期内的正余弦值全部计算出来，角度的分辨率根据实际需求来确定，分辨率越精细，那么需要存储ROM的深度就越深，反之约小，然后将计算出来的正余弦值进行一个扩大取整保留数据精度，最后按照角度顺序依次存入ROM中。很明显，通过这种方式计算正余弦值所需要的时钟周期特别短，消耗FPGA的存储资源大。

2. 基于Cordic算法计算: Cordic算法并不直接求解正余弦值，而且通过旋转逼近的思想来进行拟合正余弦函数。该算法拟合的精度非常高，因而被广泛应用于计算机图形学、数字信号处理等领域。

Cordic算法运算过程中，只设计到移位和加减运算，这种运算是非常适合于FPGA的，从面积和计算速度两方面进行综合考虑，最终选择占用面积较小、计算速度略低的Cordic算法来求解sin/cos函数值。

首先如下图所示，假设单位圆上有任意两点Q和P，它们之间的角度关系已知，则它们的XY轴坐标可以表示如下:

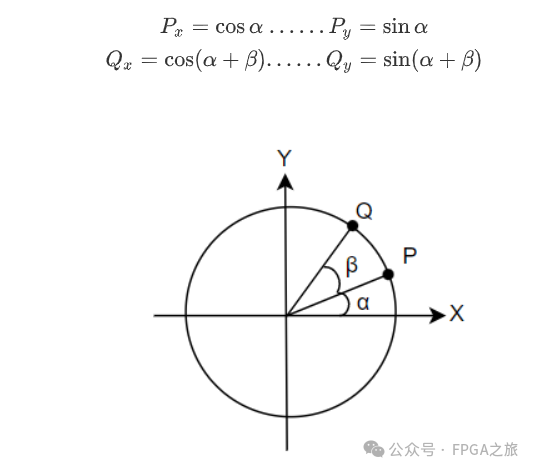
将Q点的坐标公式进行展开，然后再将P点的坐标公式代入其中可得:

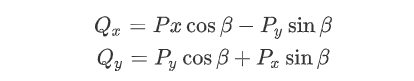
为了统一变量类型，将cos函数作为公共相提取出来，可以得到如下形式:

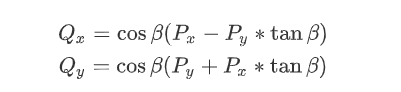
可以看出，由P点旋转至Q点后，Q点的最终表达式如上所示，这种形式便是Cordic算法旋转的基本公式了。如果将旋转初始点P设置为一个特殊位置：X轴上，那么很明显Q点的坐标值就是对应旋转角度的正余弦值。

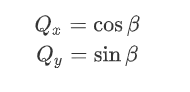
有了上述基本推论，就可以开始真正的进行旋转拟合了。P点直接一步旋转到Q点，肯定是不可取的。如果将P点经过多次旋转，每一次旋转的角度均为特殊角度,tan函数对应的角度值如下，这样就将乘法运算巧妙的转换成了左移运算。

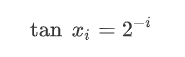
每一次旋转迭代的公式如下，每一次旋转的公式里面还包括了cos函数，这也是不方便在FPGA内计算的，观察表达式可以知道，cos函数在这里起到的作用是对坐标值起到等比例缩放的作用，并不会影响旋转的点对应向量的方向。

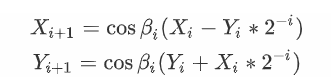
所以可以将每一次旋转过程中的cos函数提取出来，最后进行运算，这样就不用参与到每次的旋转计算中去，由于旋转的角度是已知的，所以当确定好旋转次数后，可以将这部分运算提取计算出来，作为一个系数K，K的表达式如下图所示。

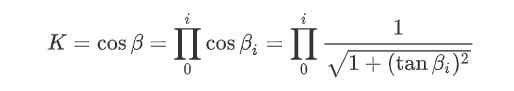
接下来就是需要研究每次旋转对应的角度值了，角度对应的tan函数值是已知的，可以通过Python直接求解出对应的角度，然后汇总成如下表格:

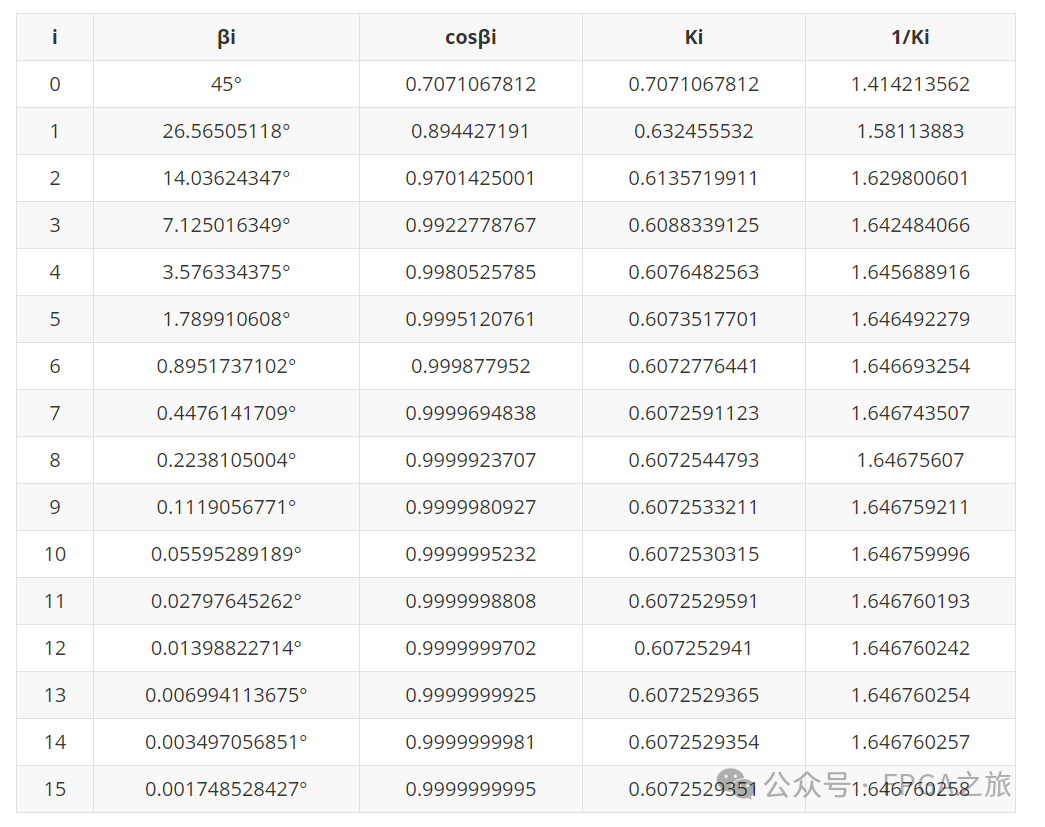
通过上表可以看出，当旋转到16次的时候，角度的误差只有千分之一了，而cosβ和K的值均趋近于一个定值，故Cordic旋转拟合是收敛的。在旋转的过程中，可能会出现旋转角度大于目标角度的情况，所以在旋转的过程中还需要增加一个变量d来控制旋转的方向，另外用z来表示旋转到的角度值，最终的旋转迭代公式如下:

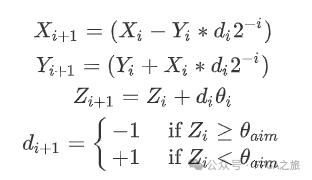
最终目标角度的正余弦值如下:

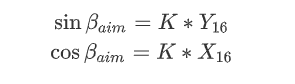
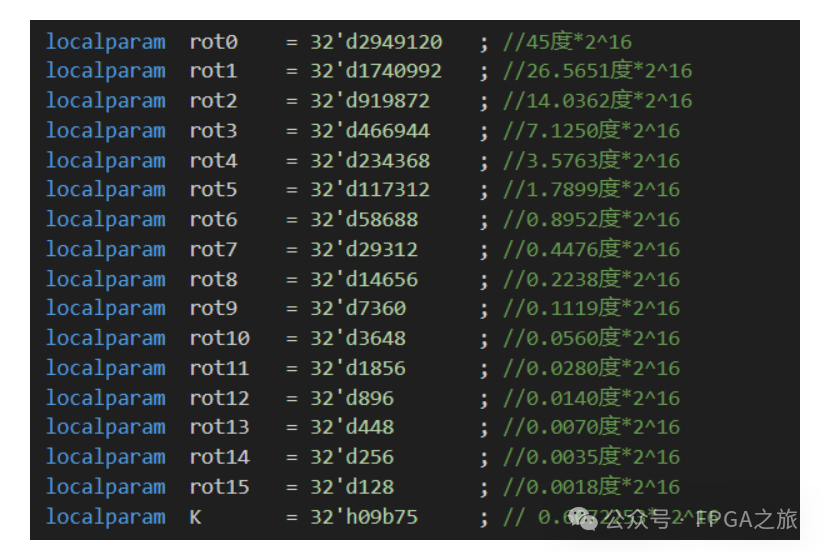
FPGA内部实现的过程中，需要对旋转角度值以及K值扩大2^16次方，然后取整，为的是在保持计算精度的情况下，免去数据的小数部分，这些都是固定值，不会根据目标角度的变化而变化，可以在程序中直接定义出来，如下图所示。

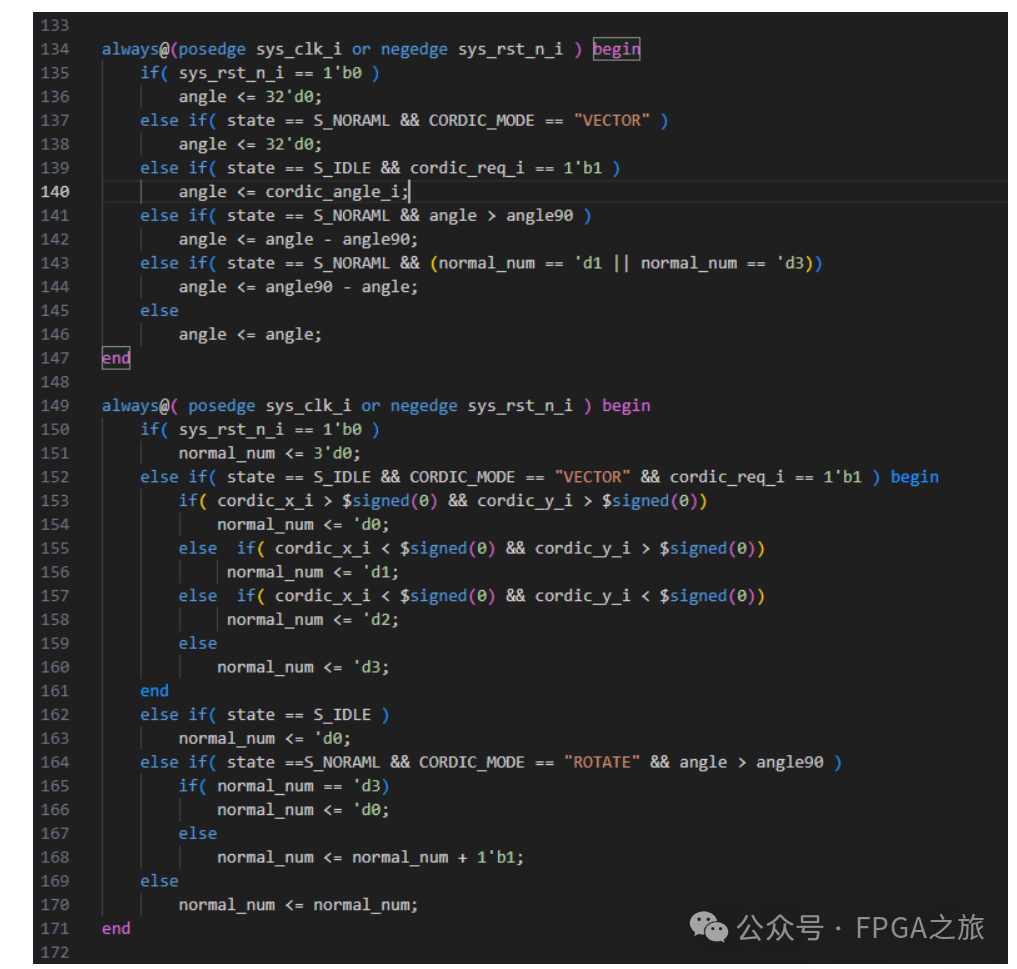
另外还要一个关键点需要注意的是迭代公式中使用的是tan函数，需要对目标角度限制在-90°到90°范围内，所以在目标角度输入模块之后，需要先对角度进行一个象限变换，为了处理的方便，本设计将目标角度变换到第一象限内，也就是0°到90°，如下图所示，象限变换不会影响正余弦数组的大小，只会影响其数值的符号，所以在迭代完成后，根据需要对坐标点进行取反运行即可。