背景介绍：
无人机、平衡车都可以通过“对姿态做pid”来控制。这里“姿态解算”对许多新人来说是个难点。
姿态解算入门系列推文从最基础的算法入手循序渐进，跟着学完会发现姿态解算原来并没有想象那么难。

姿态解算的最小依赖

惯性传感器数据是姿态解算的最小依赖。惯性传感器指：加速度计、陀螺仪。

我们回头再看一下 datasheet 上对这 6 个数据的图形表述：

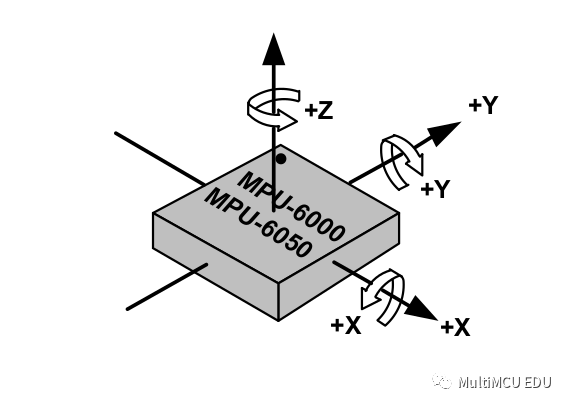
6 个独立的惯性传感数据需要经过算法的整合才能起到最大作用。“算法”两个字好像很难的样子，事实上只要认识清楚就会发现“算法”不过是一只挡路的纸老虎罢了。

笛卡尔右手系

我们最常使用的直角坐标系都符合“笛卡尔右手系”规则，右手系规则如下：

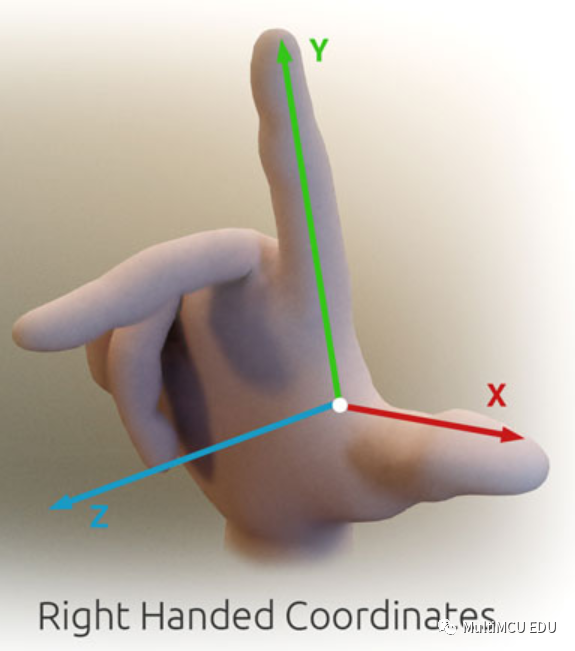
显然 MPU6050 的坐标定义也符合这个右手系规则。当前很多人工智能相关的姿态角定义都是在笛卡尔右手系下，比如：

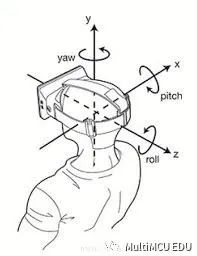
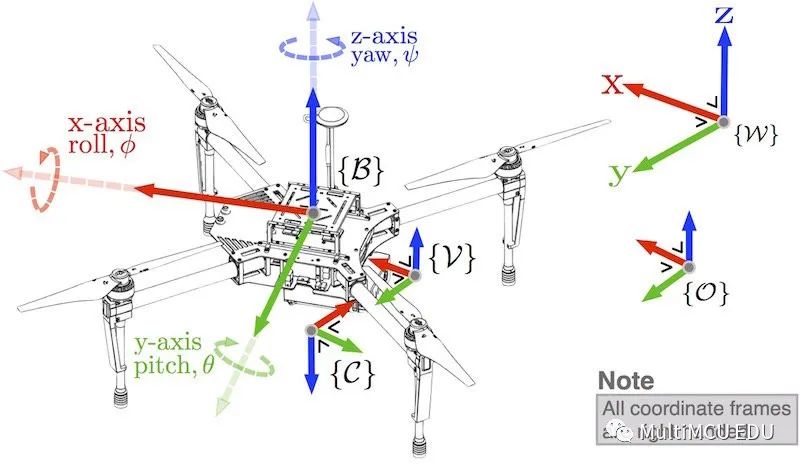
上图飞控的定义方式：绕 x 轴转为 roll、绕 y 轴转为 pitch、绕 z 轴转为 yaw。

开始第一步姿态解算

经过上面的知识铺垫我们可以开始在笛卡尔右手系下开始第一步姿态解算了，本篇我们只讲这一步，目标是：把这一步彻底弄清楚。

MPU6050 z 轴向上放置的时候，Z 方向的加速度是正 9.8 m/s/s 左右。这个地球的重力加速度就是本篇展开姿态解算的依据。

下面用二维的方式展现一下三维的笛卡尔右手系坐标，其中红色箭头就是 MPU6050 z 轴向上放置时测出的重力加速度。下面请盯住手机屏幕，硬把第一个二维图看出三维效果，并用右手验证过确实符合笛卡尔右手系规则后再往下进行。

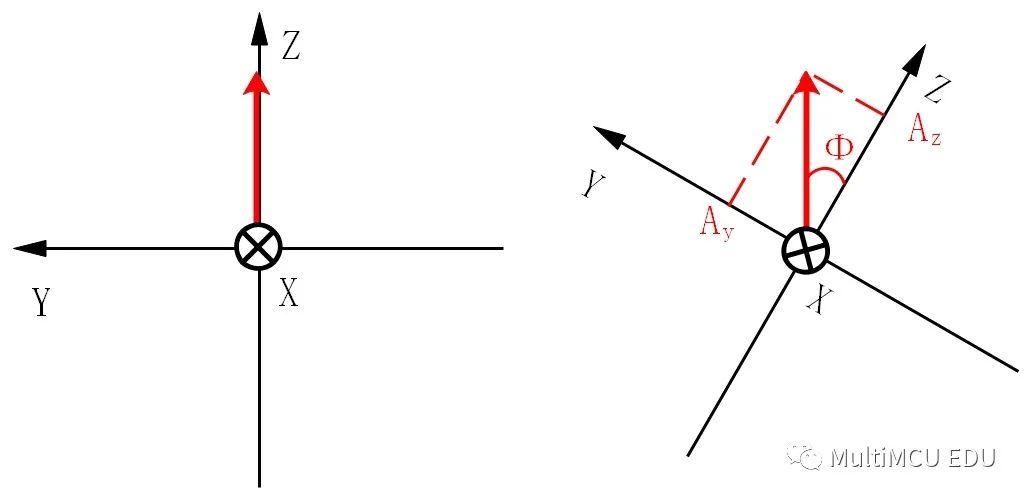
上图右侧的Ф就是 Sugar 要表示的横滚角 roll，此时 MPU6050 能够读到重力加速度在 y 轴和 z 轴上的分量 Ay 和 Az，显然：

tan(Ф) = Ay / Az，即：Ф = arctan(Ay / Az)

上面的公式就是本篇姿态解算的唯一核心内容，不难吧？

在 Sugar 习惯的 ardupilot 飞控定义下，横滚角 roll 指：重力加速度与“X-Z 平面”的夹角。上图中重力加速度在 X-Z 平面的投影正好与 z 轴重合，这是一种特殊情况。应用勾股定理推广到一般的情况是：重力加速度在 X-Z 平面的投影长度 = sqrt(Ax^2 + Az^2)。因此，我们能够得到 Ф 在三维空间内的通用公式：

Ф = arctan(Ay / sqrt(Ax^2 + Az^2))

至此我们得到了本篇用于解算横滚角 Ф 的公式。下面用同样的方法推一下俯仰角 θ 的公式。下面依然从用二维方式表示的三维笛卡尔坐标右手系入手。

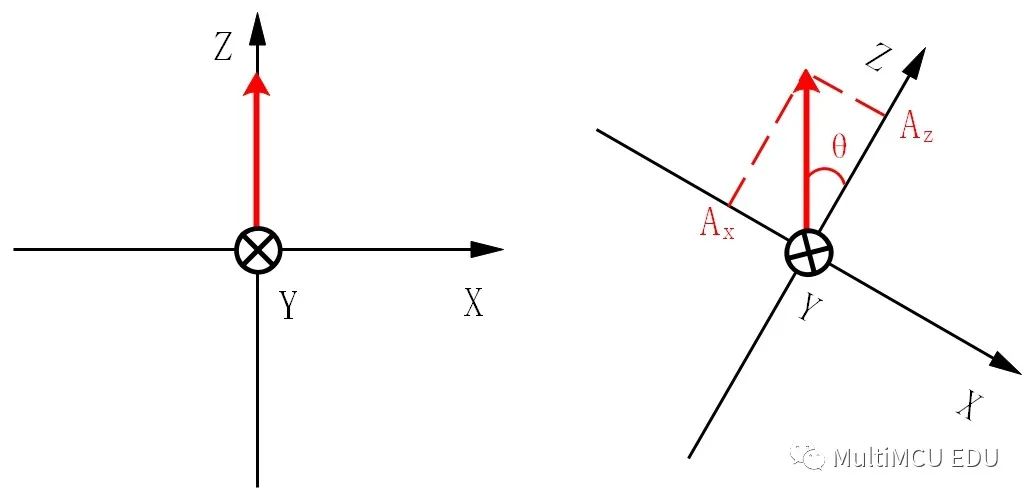
这里直接给出结果(注意坐标轴指向，这里 Ax 要取相反数-Ax)：

θ = arctan(-Ax / sqrt(Ay^2 + Az^2))

提醒：θ 表示重力加速度与“Y-Z 平面”的夹角。

姿态解算的起点 or 终点

至此，我们已经得到了需要的横滚角与俯仰角，似乎已经到达终点了。然而事实是：并没有。
本篇我们只用了 MPU6050 的加速度分量，由于加速度易受高频噪声干扰，因此算得的姿态角是很不稳定的，不能直接参与控制。

到这里已经完成了姿态解算入门系列的第二篇推文，恭喜能看到这里并理解本文内容的读者已经迈出了入门的第一步。