前言
本文用于记录学习CORDIC算法期间的收获,以供日后自己及他人参考;并且附上了使用Verilog实现CORDIC算法求解角度的正弦和余弦的代码、简单的testbench测试代码、以及在Modelsim下的仿真结果。
CORDIC的基本原理介绍
CORDIC(Coordinate Rotation Digital Computer)算法即坐标旋转数字计算方法,是J.D.Volder1于1959年首次提出,主要用于三角函数、双曲线、指数、对数的计算。该算法通过基本的加和移位运算代替乘法运算,从而实现旋转和向量计算,不再需要三角函数、乘法、开方、反三角、指数等函数。而移位和加法,很容易用纯硬件来实现,故CORDIC算法非常适合FPGA实现。
CORDIC算法可以在圆坐标系、线性坐标系和双曲线坐标系使用,从而可以演算出8种运算,而结合这8种运算也可以衍生出其他许多运算。下表展示了8种运算在CORDIC算法中实现的条件。

首先,我们先从旋转模式下的圆坐标系讲起,这也是CORDIC方法最初的用途。
-
CORDIC的几何原理介绍
假设在xy坐标系中有一个点P1(xi,yi),将P1点绕原点旋转θ角后得到点P2(xj,yj)。
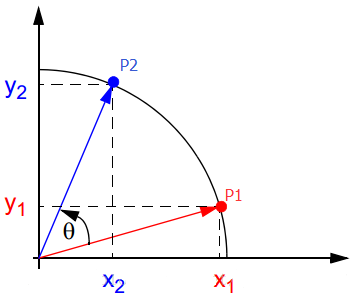
于是可以得到P1和P2的关系。
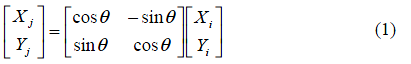
以上是CORDIC的几何原理部分,而我们该如何深入理解这个几何原理的真正含义呢?
从以上图解,我们可以知道,当已知一个点P1的坐标,并已知该点P1旋转的角度θ,则可以根据上述公式求得目标点P2的坐标。如果将上述复杂的三角运算操作转换为一种单一的“迭代位移”算法会怎么样?那么,接下来我们介绍优化算法部分。
2. CORDIC的优化算法介绍
我们先介绍算法的优化原理:将旋转角θ细化成若干分固定大小的角度θi,并且规定θi满足tanθi = 2-i,因此∑θi的值在[-99.7°,99.7°]范围内,如果旋转角θ超出此范围,则运用简单的三角运算操作即可(加减π)。
然后我们需要修改几何原理部分的假设,假设在xy坐标系中有一个点P0(x0,y0),将P0点绕原点旋转θ角后得到点Pn(xn,yn)。而旋转过程中经过n个 θi角,则相邻的两个点Pi与Pi+1之间的关系为:
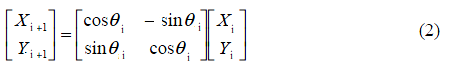
公式(2)提取cosθ,可修改为:
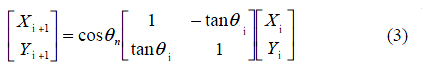
修改后的公式把乘法次数从4次改为3次,剩下的乘法运算可以通过选择每次旋转的角度去除,将每一步的正切值选为2的指数(二分查找法),除以2的指数可以通过右移操作完成(verilog)。
每次旋转的角度可以表示为:

所有迭代角度累加值等于最终需要的旋转角度θ:

这里Sn为1或者-1,根据旋转方向确定(后面有确定方法,公式(15)),顺时针为-1,逆时针为1。
Sn = {-1;+1}; (6)
可以得到如下公式:

结合公式(3)和(7),得到公式(8):
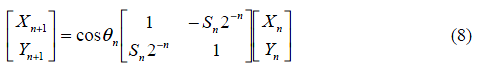
到这里,除了余弦值这个系数,算法只要通过简单的移位和加法操作完成。而这个系数可以通过预先计算最终值消掉。首先根据(4)重写这个系数如下:
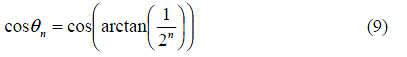
第二步计算所有的余弦值并相乘,这个值K称为增益系数。
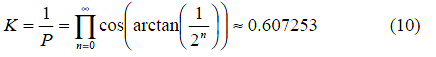
由于K值是常量,我们可以先忽略它。
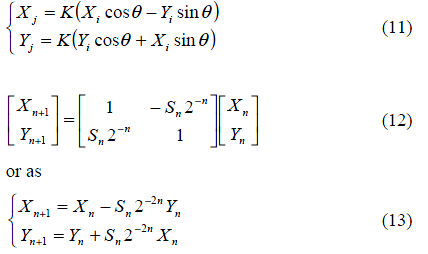
到这里我们发现,算法只剩下移位和加减法,这就非常适合硬件实现了,为硬件快速计算三角函数提供了一种新的算法。在进行迭代运算时,需要引入一个新的变量Z,表示需要旋转的角度θ中还没有旋转的角度。

这里,我们可以把前面提到确定旋转方向的方法介绍了,就是通过这个变量Z的符号确定。

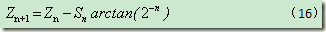
通过公式(5)和(15),将未旋转的角度变为0。
一个类编程风格的结构如下,反正切值是预先计算好的。
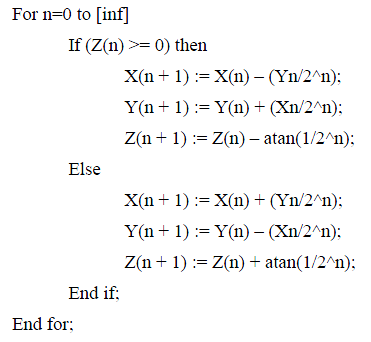
01
旋转模式:
旋转模式下,CORDIC算法驱动Z变为0,结合公式(13)和(16),算法的核心计算如下:
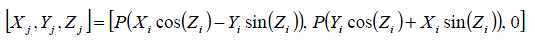
一种特殊情况是,另初始值如下:
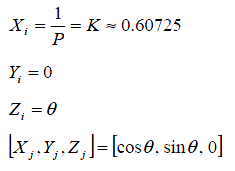
因此,旋转模式下CORDIC算法可以计算一个输入角度的正弦值和余弦值。
02
向量模式
向量模式下,有两种特例:
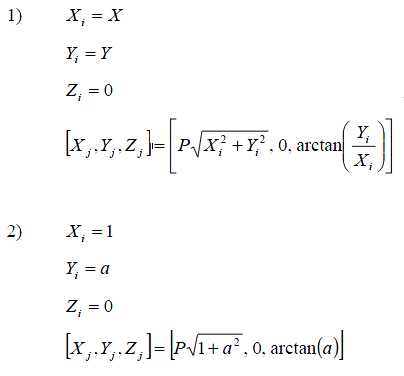
因此,向量模式下CORDIC算法可以用来计算输入向量的模和反正切,也能开方计算,并可以将直角坐标转换为极坐标。
硬件算法实现
CORDIC迭代算法的一种直接实现方式是反馈结构,此结构只设计一级CORDIC运算迭代单元、然后在系统时钟的驱动下,将本级的输出作为本级的输入,通过同一级迭代完成运算。这种方法硬件开销小、但控制相对复杂。
下面分段介绍下各部分代码:
首先是角度的表示,进行了宏定义,360读用16位二进制表示2^16,每一度为2^16/360。
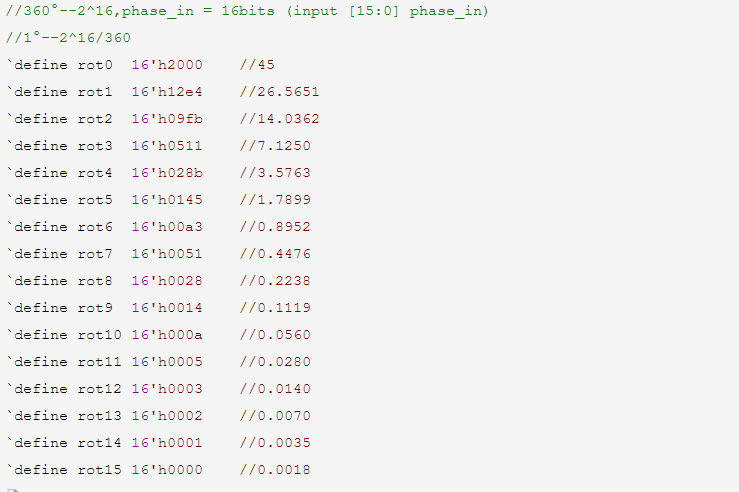
然后是流水线级数定义、增益放大倍数以及中间结果位宽定义。流水线级数16,为了满足精度要求,有文献指出流水线级数必须大于等于角度位宽16(针对正弦余弦计算的CORDIC算法优化及其FPGA实现)。增益放大2^16,为了避免溢出状况中间结果(x,y,z)定义为17为,最高位作为符号位判断,1为负数,0为正数。
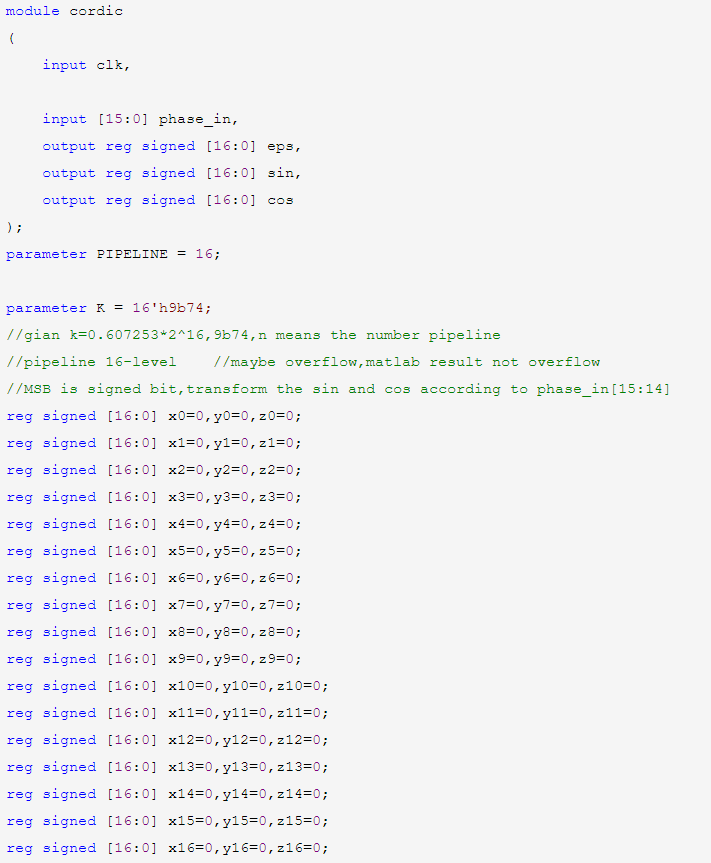
还需要定义memory型寄存器数组并初始化为0,用于寄存输入角度高2位的值。

接着,是对输入角度象限处理,将角度都转换到第一象限,方便处理。输入角度值最高两位赋值0,即转移到第一象限[0°,90°]。此外,完成x0,y0和z0的初始化,并增加一位符号位。

接下来根据剩余待旋转角度z的符号位进行16次迭代处理,即完成16级流水线处理。(见附录A完整代码)
其中使用到了算数右移(>>>)运算、所以在之前声明时将相应的reg/wire均声明为signed类型。
需要注意的是这里的算数移位运算,与之区分的是逻辑移位运算。
二者规则为:
逻辑左移和右移,空出的位均补零。
算数左移与逻辑左移相同,都在低位补零;算数右移、移出的高位比特使用符号位填充(0正1负)
举例说明,对8'b_1011_0111进行逻辑、算数移位的结果如下图所示:

比如这里的原数值是8'b10110111、为负数(补码形式)、换算成十进制为-73.
算数右移一位之后的结果是8'b11011011、由补码换算成原码再换算为十进制为-37.
由于进行了象限的转换,最终流水结果需要根据象限进行转换为正确的值。这里寄存17次高2位角度输入值,配合流水线结果用于象限判断,并完成转换。

最后,根据寄存的高2位角度输入值,利用三角函数关系,得出最后的结果,其中负数进行了补码操作。
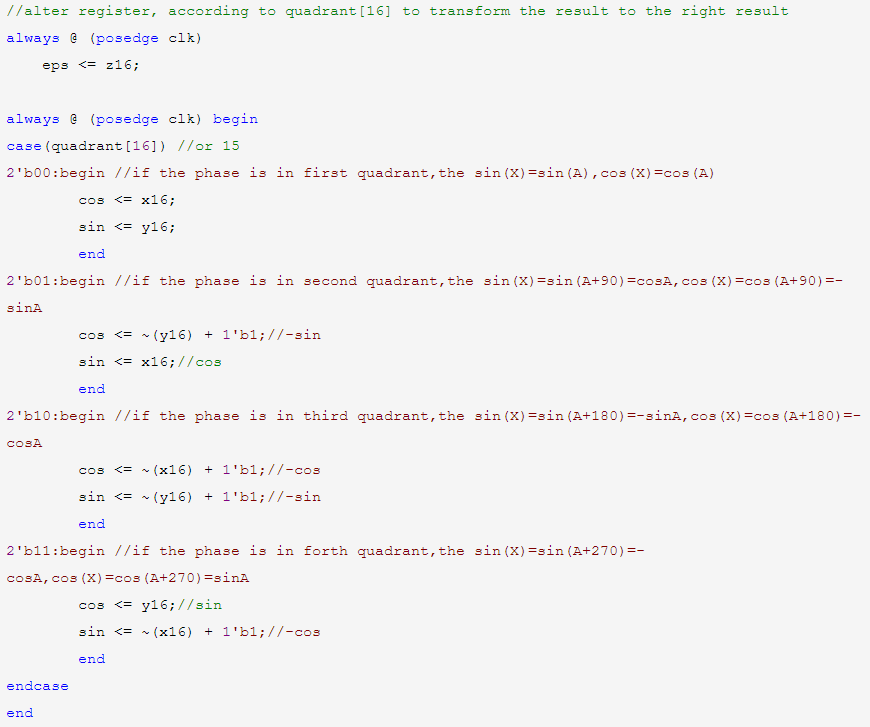
完整代码及 testbench代码见附录A
Modelsim仿真结果
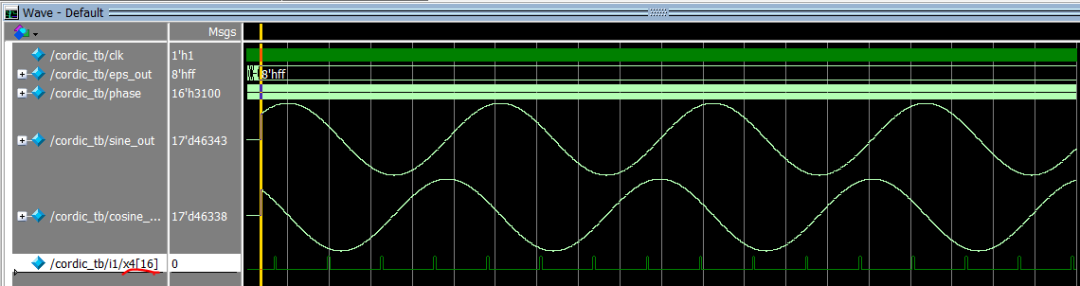
仿真结果的补充说明:
(1)程序全程未使用复位信号,testbench中第一个计算的角度为16'h2000也就是45度,如果以图示时刻为0时刻、仿真结果对应的波形即分别为sin(x+π/4)和cos(x+π/4)的波形。作为参考,0.5*√2*65535≈46340.
(2)关于运算过程中的位数溢出
根据仿真结果,本测试例下,x4出现过16位位数溢出。
(3)关于流水线设计的理解
前文提到过实现CORDIC迭代算法时可以使用反馈结构(只使用一级)、也可以使用流水线结构(多级),如果任务是只单独计算一个角度的正弦或者余弦值,那么所需要的迭代次数或者说消耗的时钟周期数量其实是相同的,本设计中为16个时钟。
流水线结构的威力是在连续、源源不断地计算一组多个角度的正余弦值的时候才展现出来,当初始流水线被填满之后,每经过一个时钟周期、都会在输出上获得一个更新的角度的正余弦结果值,上图仿真结果图中黄色cursor左侧的时间段内、流水线即被逐步填满。
换句话说,如果现在的任务是要计算n个角度的正余弦值、计算一个角度需要的迭代次数为x,反馈结构需要的时长为(n*x)个时钟周期,流水线结构只需要(n+x-1)个时钟周期。


 0
0







