1、什么是 PID 呢？
PID算法是一种闭环控制算法，它由比例（proportional）、积分（integral）、微分（derivative）三部分控制算法单元组成，是一种常见的用于保持目标参数或者目标对象稳定的控制算法。理论说的有点拗口，下面会一步一步解释的。首先，我们先来理解一下过程控制的思路。下面是一个简单的闭环控制系统的框图：
所以，上图中的调节器部分就是我们为了被控变量达到我们预设的目标值，而又能稳定的维持要采用的控制器（算法），而PID就是其中的一种算法。
上图中将调节器的部分改动一下，改为PID控制器，就变成如下的框图：
框图中 e(t) 和 u(t) 的关系式如下：
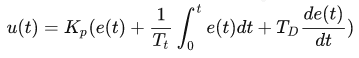将上面的传递函数展开，如下：
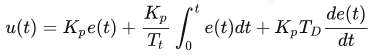然后：
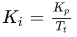
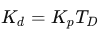由此可得：
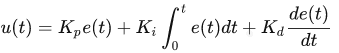
因此，上面的公式中：
Kp：比例时间系数；Ki：积分时间系数；Kd：微分时间系数；e(t)：误差t：时间
上面的式子中，把公式进行拆解，可以得到三种控制算法，每一种都可以单独使用，如下：
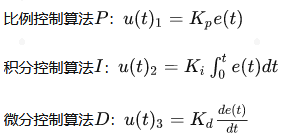从上面也可以看的出来，PID算法其实就是三个算法的组合，从数学的角度来看也就是三部分算法作用之后的的代数和！总结：PID 调节器是一种线性调节器，它将给定值 r(t)与实际输出值 c(t)的偏差的比例(P)、积分(I)、微分(D)通过线性组合构成控制量，对控制对象进行控制。
2、PID算法的 P、I、D 部分的作用和解释
（1）P - 比例的作用
比例P的作用：能够即时成比例的反映控制系统的偏差信号e(t)，一旦有偏差的产生，调节器能立即产生作用减少偏差。这是什么意思呢？是不是不好理解？
简单点说：比例部分其实就是对系统设定值和输出值的偏差的放大倍数。举个例子：如果有一个电机的两端电压为U，系统采用P控制，P=0.4，设定的目标值是800，而现在的反馈值实际是1000，那么此时输出到电机两端的电压应该变为 U+0.4*(800-1000)，以此来实现调节电机速度的目的。由此也可以看的出来，P越大，电机转速回归到输入值的速度就越快，反应就越迅速，即调节的灵敏度就越高。
但是，P也不是越大越好，虽然P大的时候调节的灵敏度会变高，但是也容易导致调节之后的目标值在预设值的附近振荡，使系统稳定性下降，会造成系统不稳定。
（2）I - 积分的左右
针对上面提到的振荡的问题，引入积分是可以解决的。积分的目的其实就是对预设值和反馈值之间的偏差在时间上进行累加，从而消除系统的稳态误差，提高系统的无差度。总而言之，只要系统还存在误差，那么积分环节就会进行调节，直到系统没有误差为止。但是，积分作用也不是越强越好，积分的作用过强的话，会导致系统的调节效果出现滞后。总的来说，积分环节的作用就是反应系统的累计偏差，使系统消除稳态误差，提高无差度，只要有误差的存在，积分调节就会进行，直至无误差；
（3）D - 微分的作用
还是接着上面的电机的转速来说明，微分的存在其实就是反映电机转速的变化率，能够通过之前误差的变化预测电机转速的误差变化的趋势，具有超前调节的作用，并且D越大，超前预测的作用越明显。简单来说，微分的存在是为了预测偏差的变化趋势，产生超前的控制作用，在偏差没有形成之前，就通过微分的调节左右消除偏差，改善系统的动态性能。关于PID的知识就先简单讲这么一点点，后期再继续学习补充。下面是我在网上找到的一个关于PID的调节的一个演示，很生动的说明了PID调节过程中P、I、D三个控制参数作用到系统的调节效果，方便大家理解PID，如下：
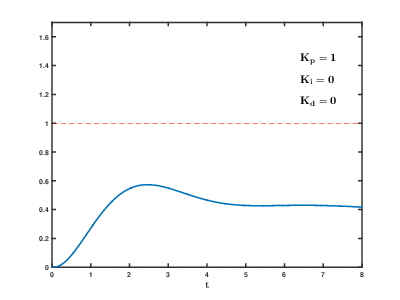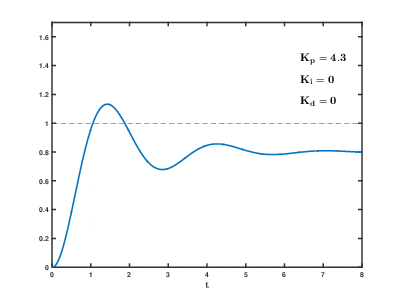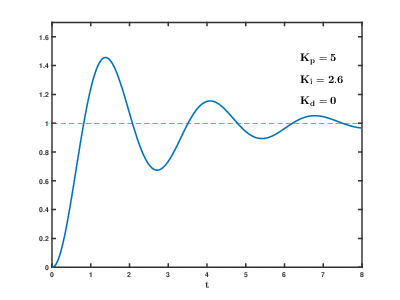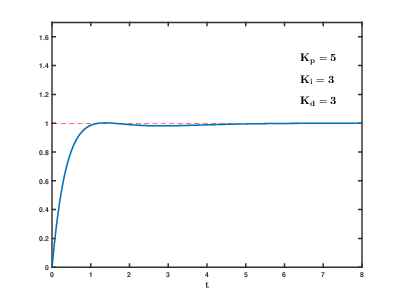从上面的动图可以看出：1、Kp越大，越能快速接近目标值1.02、只调整Kp可能会存在稳定误差3、加入Ki可以减小稳定误差，但同时也使得系统震荡加剧4、加入Ki加快了整体的响应速度5、加入Kd可以减小震荡，但也降低了响应速度(可以通过观察图像什么时间t首次碰到目标1.0)
0
