一阶RC低通滤波器很常见，课本上有详细的公式和解释，各种资料都很多。但是两个一阶RC组成的二阶RC低通滤波器，或更多RC级联，信号链上其实很常见，参见图1，但相关的资料却不是很常见。最近在ADI新出的《电路设计常见指南》中看到了相关的公式，所以这里特别记录一下。

图1 一个典型的TIA信号链（如果后级LPF截止频率与TIA一样，那么信号链的总截止频率会比第一级TIA低，所以通常后级LPF截止频率要大于TIA的至少十倍，才能符合设计目标）

一、一阶RC低通滤波器

先简单复习一下的一阶RC低通滤波器。这里我们使用TI的Analog Engineer’s calculator小工具，可以快速了解它的瞬态和频域响应。

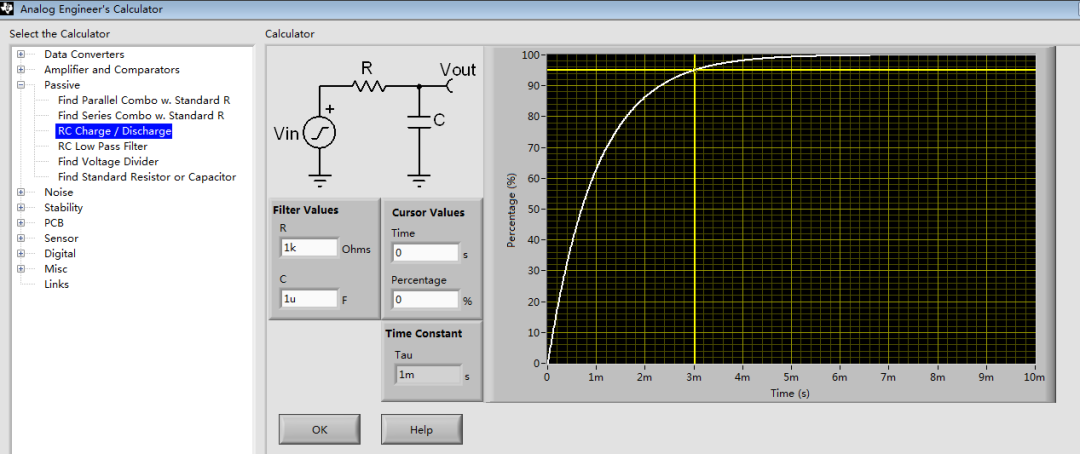
图1 一阶RC的瞬态响应（充放电时间）

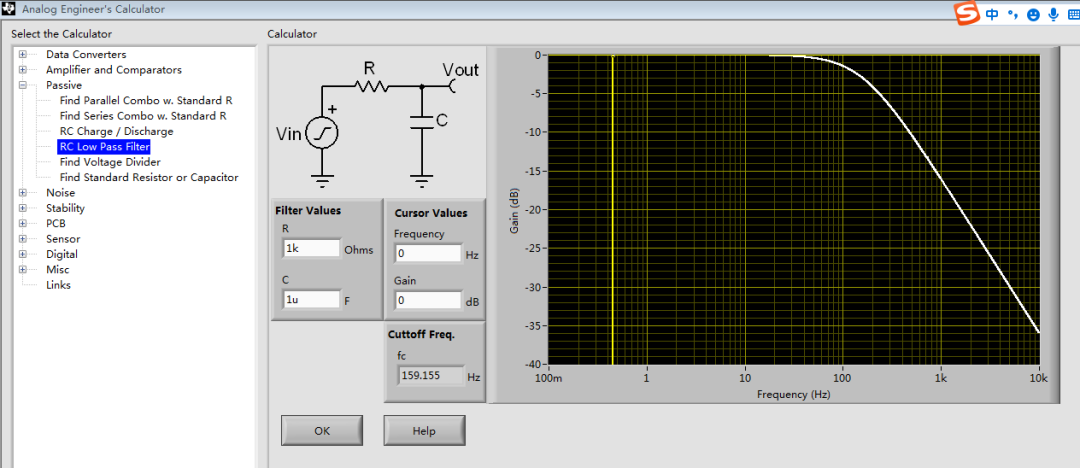
图2 一阶RC的频域响应（截止频率）

二、二阶RC低通滤波器

这里只是初步给出二阶RC低通滤波的截止频率如何计算，不会涉及公式推导等；实际上我也不太感兴趣，我现在认为会用就足够了。

图2为二阶无源RC LPF原理图和仿真结果。我们可以看到，Vo1的截止频率为180Hz，符合一阶RC低通滤波器的截止频率计算公式。后面增加一个同样截止频率的RC后，最终的截止频率变成了120Hz。借此我们知道了两阶RC级联后的总截止频率会低于一阶的。

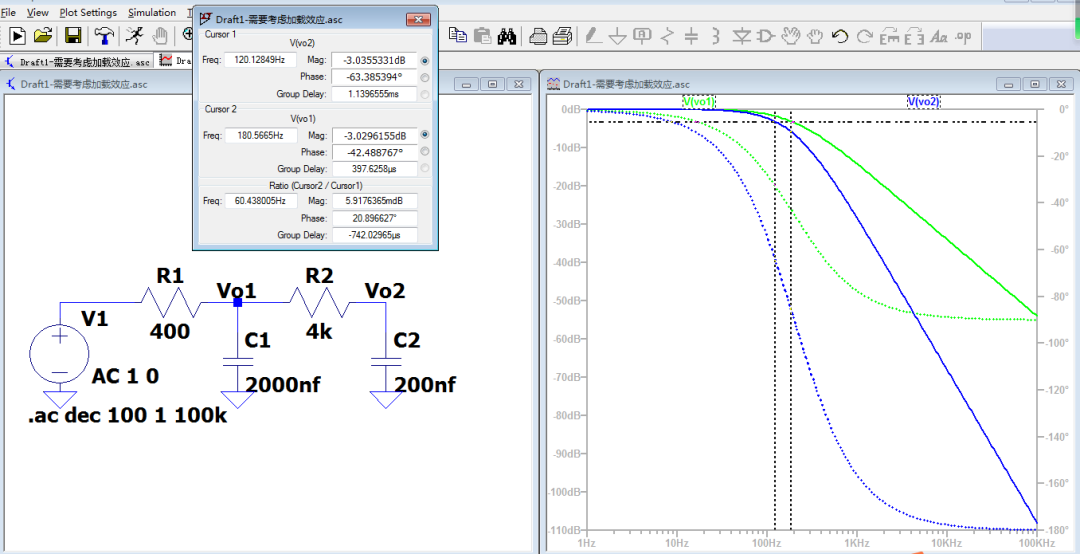
图2 二级无源RC低通滤波器

那我们怎么计算这种电路的截止频率呢？它的公式参见图3，其中n为滤波器阶数，如果是三阶或者更高，那么相应的调整公式即可；代入公式后得到的结果跟仿真是一致的。

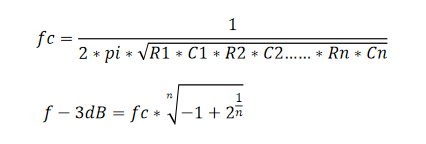
图3 二阶RC低通滤波器的截止频率计算公式

应该注意的是，这种电路设计要考虑加载效应。它的意思是，后级RC可能会成为前级的负载（主要是R）。所以一般后级R是前级的10倍，相应的，C应是前级的1/10，像图2那样。否则，截止频率跟按照图3公式计算得到的会有差异，参见图4。

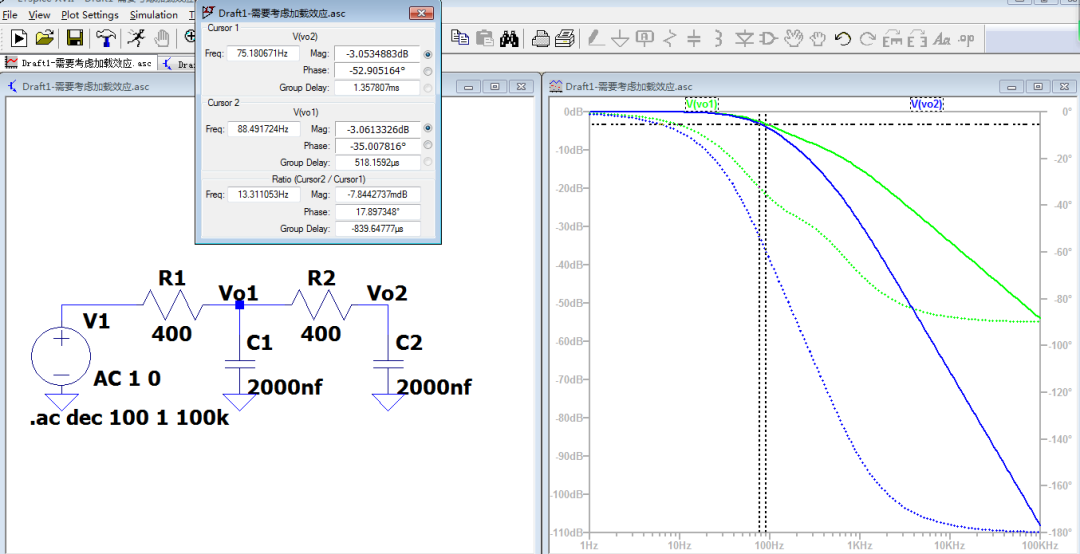
图4 未考虑加载效应的二阶LPF仿真结果，小于公式计算得到的结果

但如果是图5这种有运算放大器的二阶RC低通，那么是无需考虑加载效应的，结果与按照公式计算的一致。

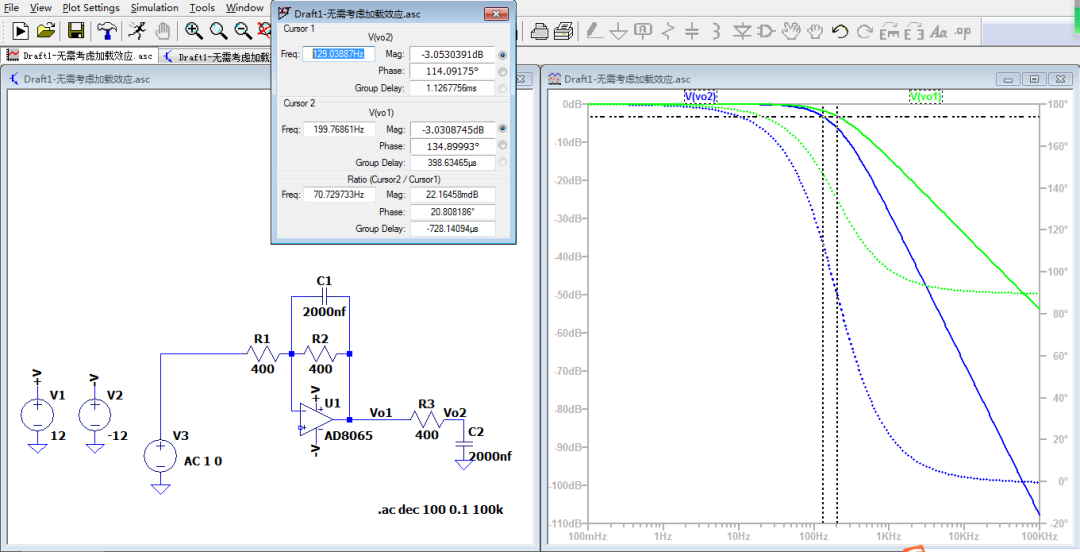
图5 无需考虑加载效应的二阶RC LPF

三、RC滤波器中的取值

这里简单总结一下我积累的RC滤波器取值的经验。截止频率固定的情况下，电阻R取值一般主要考虑热噪声和功耗，二者是没法兼得的。电阻R取值大，电容C可比较小。好处是功耗会比较低，电容C可以选型NP0材质的，因为它比较小（NP0材质电容温度和偏压特性都比较好，用于SAR型ADC驱动时特别推荐）。电阻R取值小，电容C需较大才能满足需求。此时，功耗会比较差，但是噪声性能会好。

四、总结

本文主要是整理了二阶无源RC LPF截止频率如何计算，三阶或者更多阶也是一样的公式。但如果是仅有无源RC搭建的多阶滤波器，需要考虑加载效应。