摘要：近年来，为了减小电动汽车系统中DC-DC转换器的尺寸、重量和成本，集成车载充电器（OBC）将OBC转换器与低压DC/DC转换器（LDC）结合在一起受到关注。本文提出了一种新的集成OBC转换器，具有车网互联（V2G）和辅助电池充电功能。在所提出的集成OBC中，OBC由带主动钳位电路的双向全桥转换器和带相移全桥（PSFB）及正激的混合LDC转换器组成。所有主开关都能实现零电压开关（ZVS），滞后开关几乎能实现零电流关断（ZCS），适用于所有工作条件。在所提出的LDC转换器的次级侧，采用由电容和两个二极管组成的附加电路来钳位整流二极管上的振荡电压并消除环流。由于正激转换器的输出电容与辅助电池充电器的输出电容串联连接，因此在续流期间可以将来自动力电池的能量传递至辅助电池，并且有助于减少输出电感器的电流纹波 ，导致输出电感体积更小。为了验证所提出拓扑的性能，设计了一个1 kW的原型转换器。实验结果表明，所提出电源转换器的最大效率达96%。

一、简介：

电动汽车（EV）和插电式混合动力电动汽车（PHEV）中的储能系统通常由两种电池组成（400 V 高压电池和 24 V 或 48 V 低压电池）。一种是动力电池，为电动机提供高直流电压；另一种是辅助电池，为照明、娱乐、信号电路和音频系统等低压电气设备提供低直流电压。为了给这两个电池充电，通常需要两个不同的转换器：用于动力电池的车载充电器（OBC）和用于辅助电池的低压直流/直流转换器（LDC）转换器。在EV或PHEV上的传统DC-DC转换器系统中，由于这两个转换器单独工作，所以DC-DC转换器系统的尺寸变得庞大。为了解决这个问题，人们推出了集成OBC，将OBC转换器与LDC转换器相结合，以实现更小的体积、更轻的重量和更低的成本。集成 OBC 转换器可以执行三种不同的功能：(1) 从电网到车辆 (G2V) 的充电操作、(2) 从车辆到电网 (V2G) 的放电操作和从动力电池到辅助电池的充电 。

OBC可分为两类：两级OBC和OBC转换器。在两级 OBC 转换器中，非隔离升压转换器普遍用于PFC级 。对于DC-DC转换器采用隔离转换器拓扑，例如相移全桥 (PSFB) 转换器 、双有源全桥 (DAFB) 转换器 和谐振转换器 等。在单级 OBC 转换器中，ACDC 转换器和 DC-DC 转换器相结合，利用单个电感器实现所有操作模式（制动、充电和驱动）。然而，使用单个电感器会导致直流母线电容器包含低频电压纹波并引起电池的振荡电流。此外，单级 OBC 转换器的使用存在安全性问题，因为它们无法实现电网和电池之间的电流隔离。

集成 OBC 转换器的推出是为了最大限度地减小电动汽车系统中 DC-DC 转换器的尺寸和体积，这是提高电动汽车燃油经济性的关键因素。然而，集成OBC转换器的主要问题之一是，要使集成OBC转换器中的LDC转换器具有与独立LDC转换器一样的性能并不容易。可以采用LLC谐振转换器作为LDC转换器来为低压电池充电。然而，由于动力电池的输入电压变化较大，通常为250 V至500V，LLC谐振转换器需要在大范围内改变其开关频率，这导致效率较低。也可以使用两个串联的全桥（FB）转换器的车载充电机。然而，LDC转换器的效率不够好，因为两个串联FB转换器的许多组件的连接路径较长，导致传导损耗较高。另外，由于该变换器的变压器匝比为双向应用而选择接近1，因此降压比主要取决于全桥变换器的占空比。因此，占空比越小，变换器的环流就越大，从而由于较高的传导损耗而导致变换器的效率较低。当然还可以采用高匝数变压器的三次绕组以避免小占空比运行，然而，其缺点在于，当变压器的两个次级绕组处的电压不匹配时，可能会失去软开关特性。

本文会介绍一种新型集成 OBC和LDC的方案 ，如图 1 所示。可实现双向OBC的功能 。

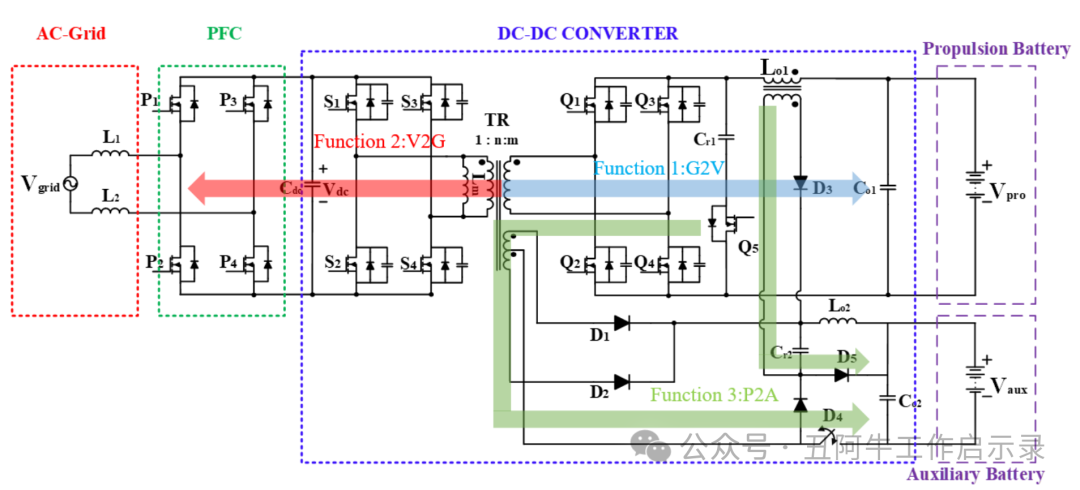
图1、新型集成OBC

二、集成OBC的LDC

集成 OBC 的 LDC 转换器电路图如图 2 所示。初级侧由输入电容器 Co1、带 Cr1 的有源钳位电路和有源开关 Q5 以及和开关 Q1、Q2、Q3 和 Q4 的 移相全桥组成。移相全桥的变压器为 TR1，其磁感为 Lm1，漏感为 L1k1，匝数比为 n1:1。正向转换的变压器为 TR2，磁化电感为 Lm2，漏感为 L1k2，匝数比为 n2:1。移相全桥的次级侧包括整流二极管 D1 和 D2，以及由 Cr2、D4 和 D5 组成的无源缓冲电路。与输出电感器 Lo2 并联的电容器 Cr2 也起到了正向转换输出电容器的作用，可降低输出电流纹波。每种工作模式的关键波形和等效电路分别如图3和图4所示。为简化起见，除开关的输出电容外，所有电路元件均为理想元件，且假设所有开关的输出电容相同。

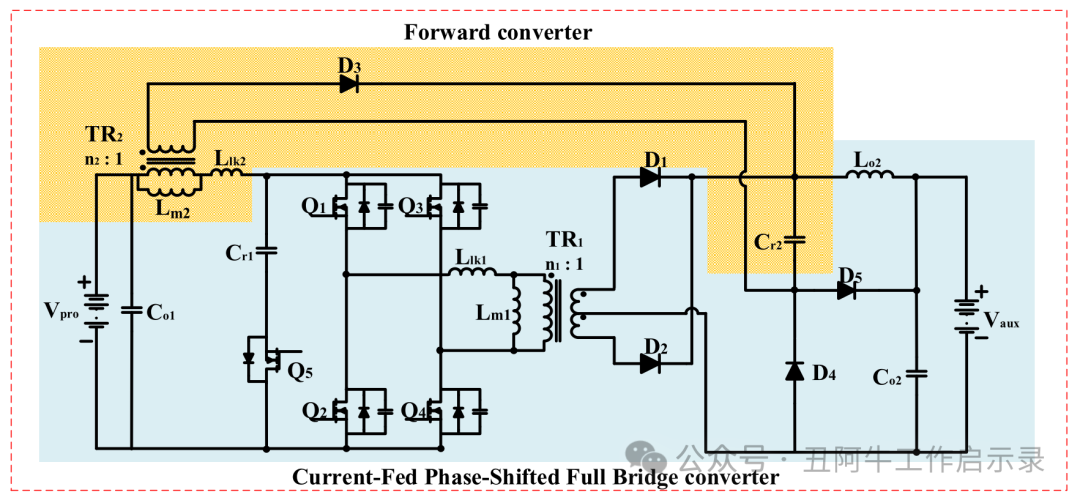
图2、集成OBC的LDC

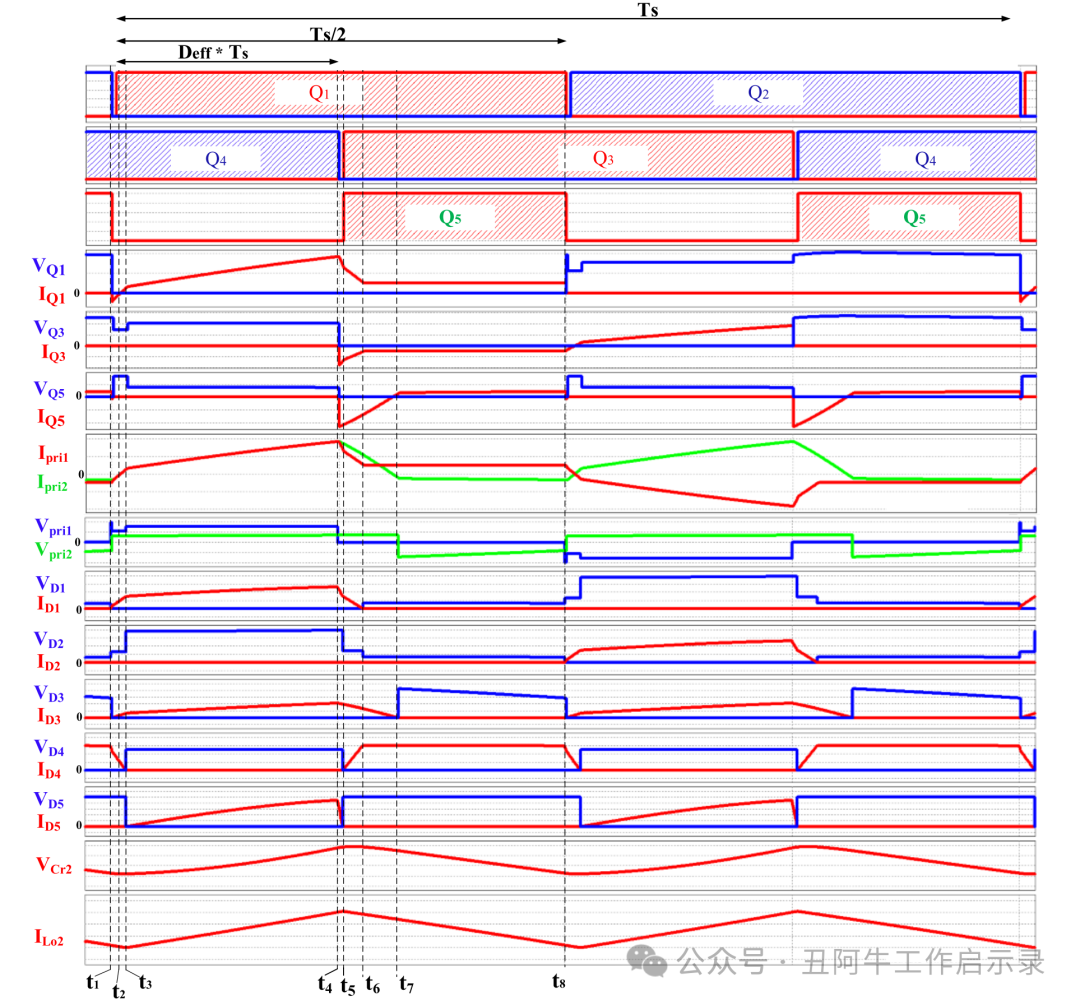
图3、LDC的关键波形

模式 1 [t1–t2]，如图 4a。

在 t = t1 时，Q4 导通，Q3 截止。Q2和Q5关断，它们的寄生电容被充电。Q1的寄生电容放电，其体二极管正向偏置，为 Q1 创造 ZVS 导通条件。功率通过变压器TR1和TR2传输到负载。

在次级侧，二极管D2和D5反向偏置。D1、D3 和 D4 为正向偏置。谐振电容器 Cr2 与输出电感器LO2 谐振并将能量释放到输出。

模式 2 [t2–t3]，图 4b。

在 t = t2 时，Q1 导通，而 Q4 在模式 1 下已导通。Q2、Q3 和 Q5 关闭。Q1 的体二极管反向偏置，电流流过 Q1。次级侧的工作方式与模式 1 相同。由于 Cr2 和 LO2 之间的谐振，流经 D4 的电流降至零，并在此模式结束时实现 D4 的 ZCS 关断。

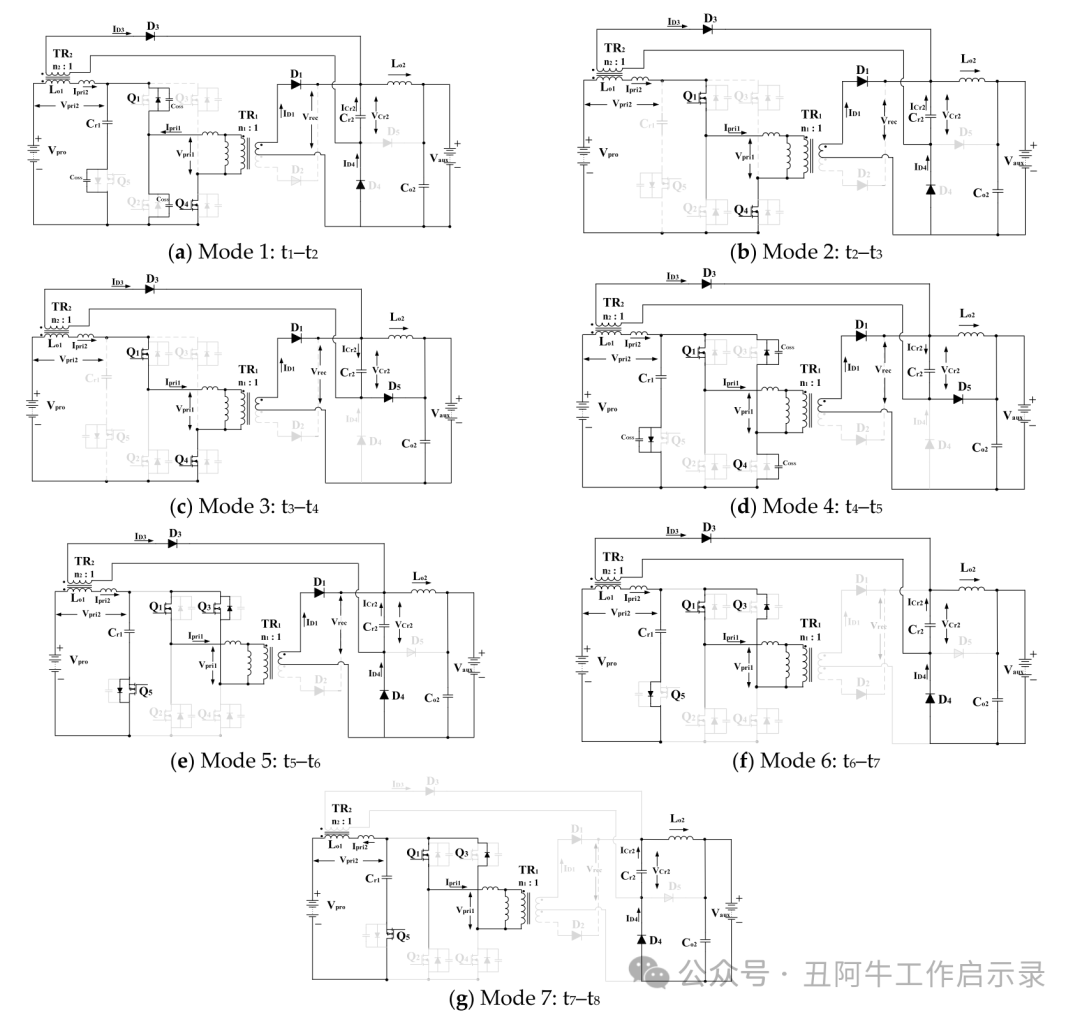
模式3 [t3-t4]，如图4c所示。

在 t = t3 时，Q1 和 Q4 导通。Q2、Q3 和 Q5 截止。两路共同将输入功率传递到输出端。在正向变换器（Forward Converter）中，原边电流 ipri2(t) 流经变压器 TR2，并给次级侧的谐振电容 Cr2 充电。在相移全桥变换器（PSFB Converter）中，原边电流 ipri1 流经开关 Q1、Q4 和变压器 TR1。原边电流 ipri1 和 ipri2(t) 的计算如下所示。

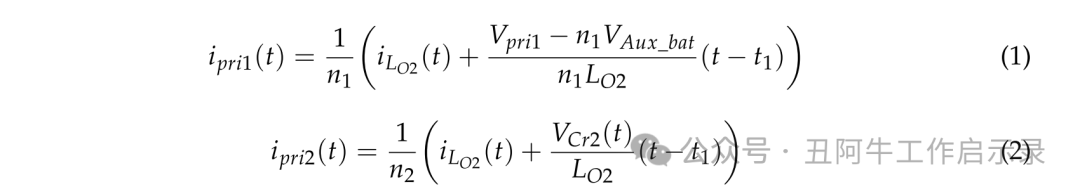
其中，Vpri1 是变压器 T1 的原边绕组电压，Vaux_bat 是辅助电池电压，ipri1 是正向变换器的原边电流，ipri2 是相移全桥变换器的原边电流，iLo2 是流经输出电感 Lo2 的电流，Vcr2 是电容 Cr2 的电压。

在次级侧，二极管D4反向偏置，D5正向偏置，分别对谐振电容器Cr2和输出电容器Co2充电。整流电压Vrec(t)可按式(3)计算。

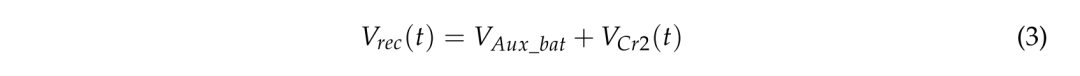
其中 Vrec 是 PSFB 转换器的整流电压。

模式 4 [t4–t5]，图 4d。

在 t = t4 时，开关 Q4 关断。Q3的寄生电容开始放电。在正激变换器中，变压器TR2的电流流过包括电容器Cr1和Q5的体二极管的有源钳位电路。电容器Cr1与漏感器LlK2谐振。由于Q4的寄生电容被充电，而Q3的寄生电容放电，因此实现了Q3的ZVS开通。Q3 两端的电压 Vcoss_Q3 如(4)可得。

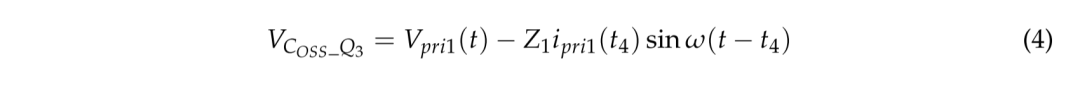
其中 ω 和 Z1 可以分别使用 (5) 和 (6) 计算。

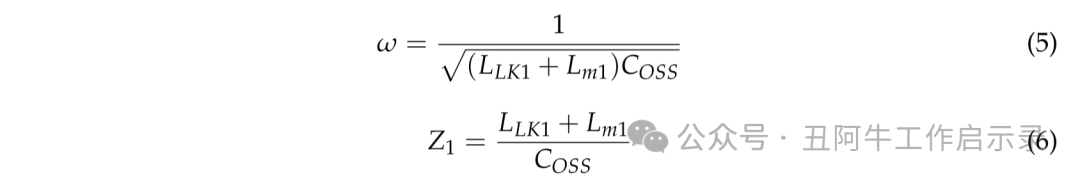
在次级侧，电流换向发生在D1与D4和谐振电容器Cr2之间。流过D1的电流iD1可以如下。

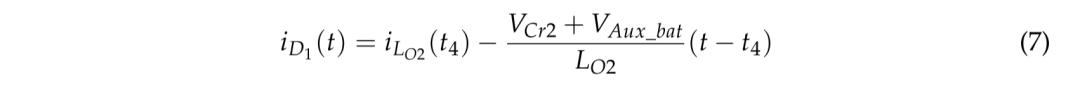
模式 5 [t5–t6]，图 4e。

在 t = t5 时，Q3 和 Q5 导通，同时 Q1 导通。Q3和Q5的体二极管以及二极管D1、D3和D4都是正向偏置的。其他二极管是反向偏置的。谐振电容器Cr2通过二极管D1和D4放电。在正激转换器中，电容器Cr1和漏感器LlK2之间的谐振继续。功率通过正激变换器的变压器TR2传输到次级侧。PSFB转换器的初级电流ipri1(t)可以用式(8)表示。

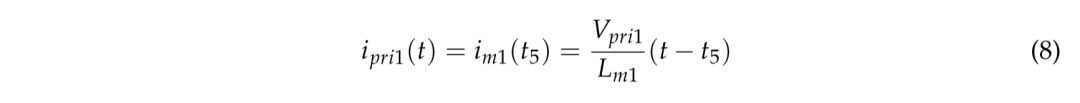
其中 im1 是 PSFB 转换器的磁化电流。

通过二极管 D1 的电流可以用式（9）表示。

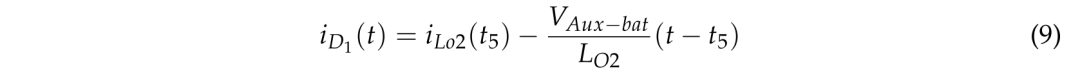
模式 6 (t6–t7)，图 4f。

在 t = t6 时，随着从 D1 到 D4 的电流换向完成，二极管 D1 反向偏置。在 PSFB 转换器的初级侧，Q1 导通，Q3 的体二极管正向偏置。PSFB 转换器的初级电流循环并保持恒定。正激转换器的工作方式与模式 5 相同。

在次级侧，二极管D3和D4正向偏置。由于LO2放电，流经D3的电流逐渐减小至零。在此模式结束时，二极管 D3 通过 ZCS 关闭。

模式 7 (t7–t8)，图 4g。

在 t = t7 时，Q5 的体二极管处于反向偏置状态，电流通过 Q5。在正向变换器中，电容 Cr1 与变压器 TR2 的电感进行谐振，谐振电流将其复位，从而消除了正向变换器对第三绕组的需求。相移全桥变换器的原边电流仍然通过 Q1 和 Q3 的体二极管循环。在此模式下，没有功率传输到次级侧。与模式 6 类似，二极管 D4 仍处于正向偏置状态，电容 Cr2 中的能量被释放到负载。在模式 7 之后，开关周期的另一半对称运行。

三、特点和设计考虑

1、转换器的特点

（1）、高降压电压转换比

LDC转换器是正激转换器和PSFB转换器的组合，具有高降压电压转换比。为了解释所提出的 LDC 转换器在电压转换比方面的特性，其简化电路模型如图 5 所示。

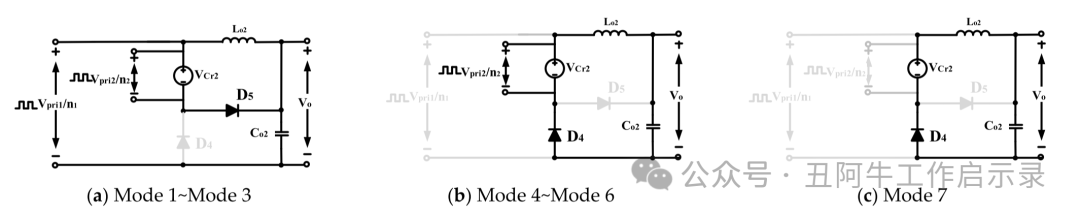
图5、LDC转换器的简化电路模型：(a) 两个转换器中的功率传输模式；（b)、正向变换器中的功率传输模式和相移全桥变换器中的自由运行模式；（c）、两个转换器的续流模式

基于图 5a 所示的等效电路，可以推导出所提出变换器的输出电压 Vo，如公式 (10) 所示。

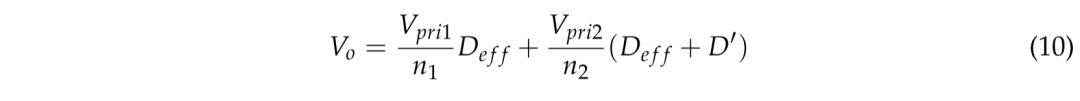
其中，Deff 是相移全桥变换器的有效占空比，D' 是模式4到模式6（t4–t6）期间的时间段，在此期间，谐振电容 Cr2 与变压器 TR2 的漏感 LlK2 进行谐振，r如公式 (11) 所示。

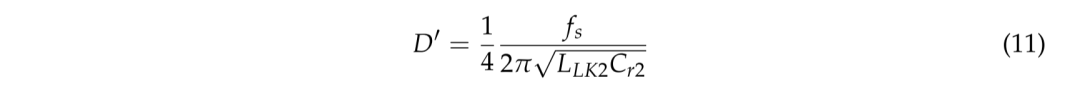
所提出转换器的电压转换比由 n1 和 n2 的匝数比决定，如图 6 所示。

施加到每个变压器的初级绕组的电压可以分别表示为(12)和(13)。

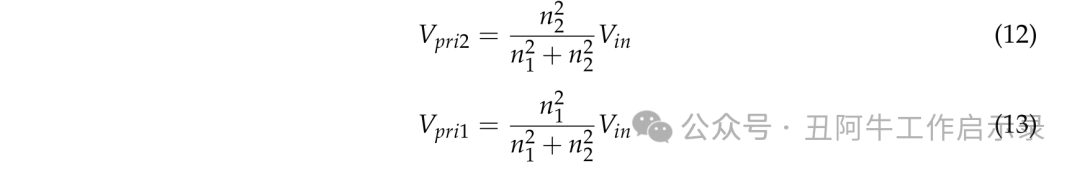
其中Vpri2是变压器TR2的初级绕组电压，VPri1是变压器Tr1的初级绕组电压。通过结合(12)和(13)，可以如(14)中那样计算所提出的转换器的电压转换比Mpropose。

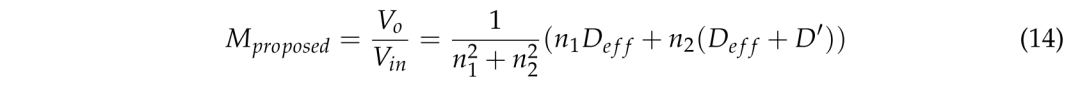
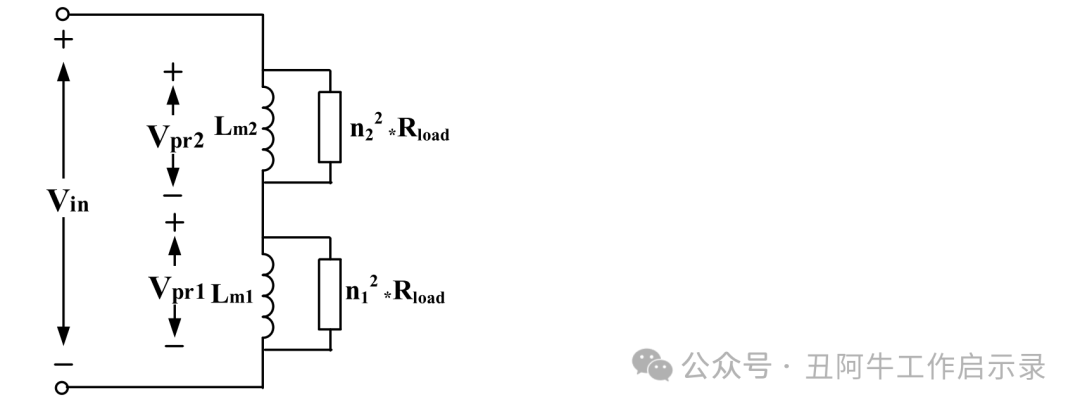
图 6. 所提出的LDC（低占空比转换器）电压转换比的等效电路。

（2）、消除环流

在传统的相移全桥（PSFB）变换器中，循环电流损耗在自由运行间隔内会降低功率转换效率，特别是当变换器工作在较小的有效占空比 D 时。相比之下，本文所提出的变换器由于增加了由 Cr2、D4 和 Ds 组成的吸收电路，可以消除循环电流。图7展示了传统 PSFB 变换器与本文所提出变换器在循环电流方面的差异。正如在模式4和模式5的操作中所述，由于谐振电容 Cr2 被放电并且二极管 D1 和 D4 处于正向偏置状态，初级电流在自由运行期间迅速减少，从而减少了循环电流。因此，几乎可以实现 PSFB 变换器滞后桥臂开关的零电流关断（ZCS）操作。

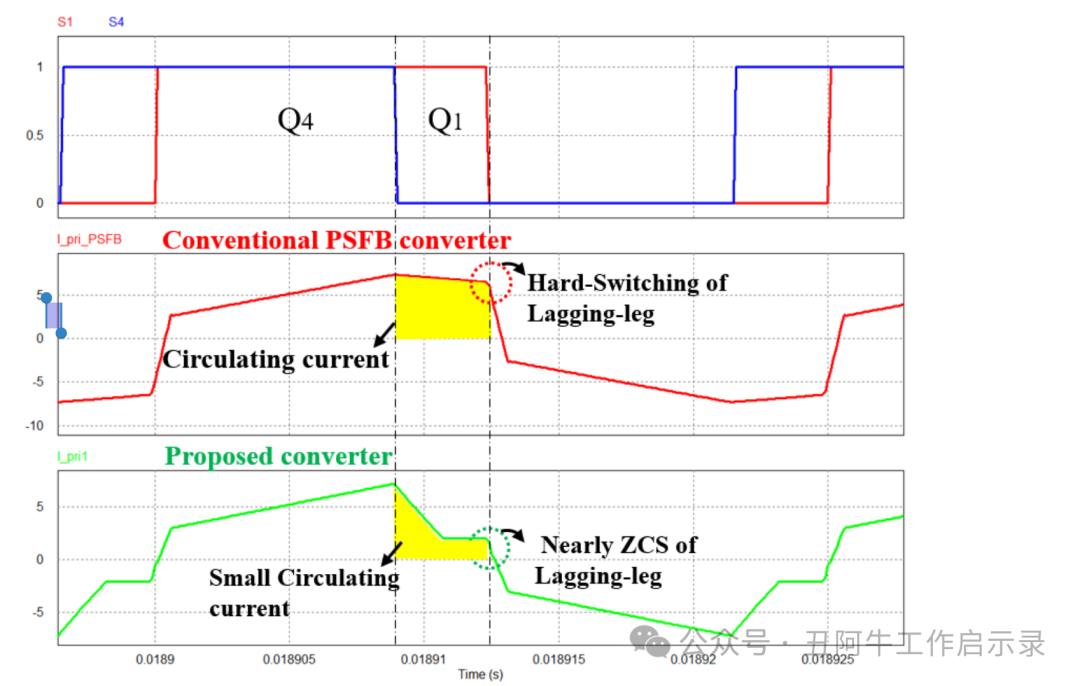
图 7. 传统 PSFB 变换器与本文所提出变换器中循环电流的比较。

（3）、输出电流纹波小

对于传统的 PSFB 转换器，在供电期间施加到输出电感的电压幅度与续流期间相同，如图 8a 所示。然而，在本所提出的转换器中，由于正激转换器的操作，如模式 5 至模式 7 中所述，由于二极管 D5 反向偏置，续流期间施加到输出电感器的电压会降低，如图所示 8b. 因此，可以显著降低输出电感的电流纹波

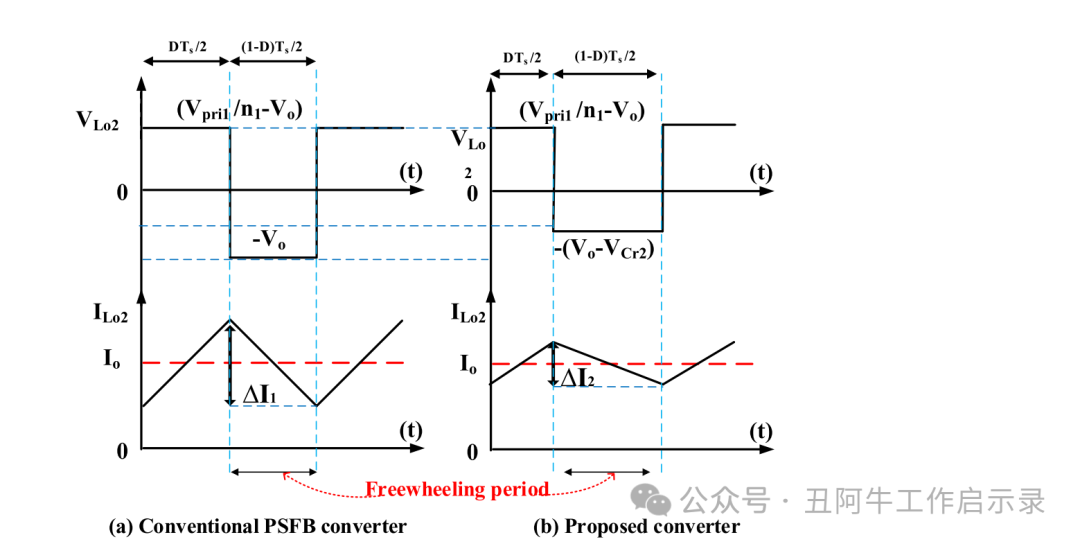
图 8. 传统 PSFB 转换器和本文方案的输出电感器处的电压和电流波形

在传统 PSFB 转换器中，输出电感的纹波电流 ΔI1(Conventional_PSFB) 可以使用 (15) 确定。

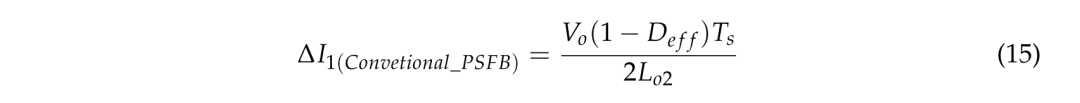
本文所提出转换器中输出电感器的电流纹波 ΔI2(Propose_Converter) 可按 (16) 计算。

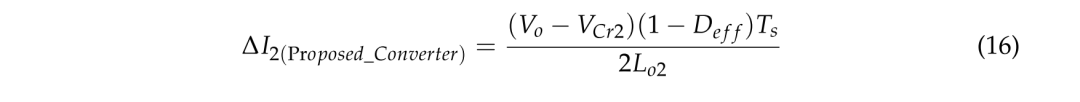
这两种情况之间的电流纹波之比Rripple 可按式（17）计算。

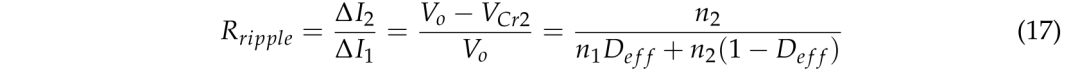
图 9 显示了具有不同有效占空比值的两种情况之间的电流纹波比率。当动力电池的电压为 420 V 时，LDC 的占空比为 0.9，本文所提出的转换器的输出电感器 LO2 的电流纹波仅为传统 PSFB 转换器的 29%。当动力电池电压为250 V时，输出电感LO2的电流纹波仅为传统PSFB转换器的47%。因此，可以显著减小输出滤波电感LO2的值和尺寸。

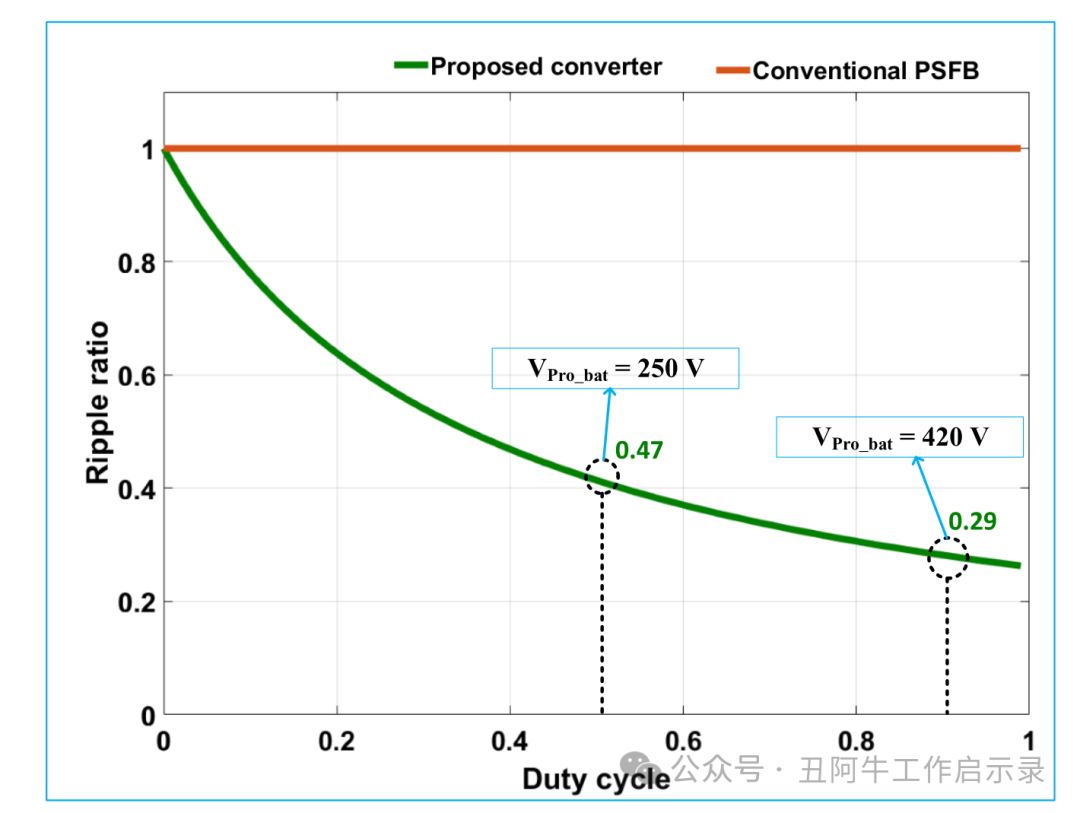
图9、本文所提出变换器与传统拓扑相比的电流纹波比率

2、设计参考

（1）、PSFB中所有开关在整个负载范围内实现ZVS的条件

为了实现MOSFET的ZVS（零电压开通），变压器TR的励磁电流