前面的文章将基2FFT、基3FFT、基5FFT的算法和实现都写完了(基2FFT的verilog代码实现及仿真,基3FFT的verilog代码实现及仿真,基5FFT的verilog代码实现及仿真),本文开始研究IFFT的实现。
直接上公式,观察离散傅里叶公式(DFT)和傅里叶逆变换的公式(IDFT):
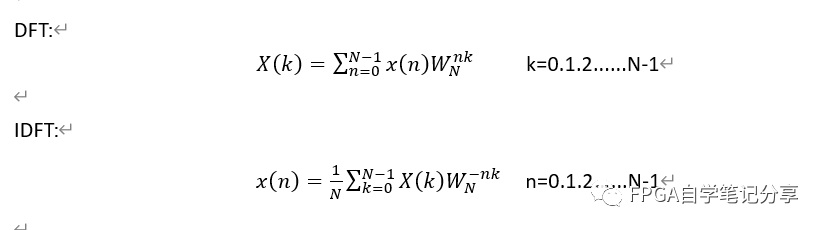
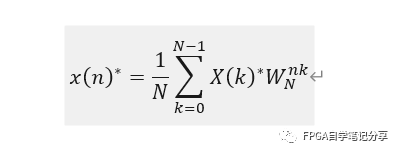
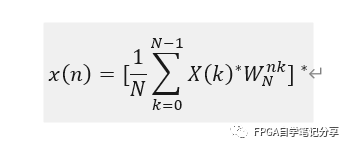
- 将X(K)取共轭得到X*(K)
- 将X*(K)进行FFT运算
- 对FFT的结果取共轭,并除以N得到x(n)
首先是python代码的修改:将基2FFT的算法推导及python仿真中的代码增加一个参数,并在数据进入蝶形运算之前首先对其进行判断然后取共轭:
IFFT_flag = 1 #1 表述求 ifft if IFFT_flag : data[0] = data[0].conjugate()最后将倒序后的输出增加判断,如果是IFFT对输出结果求共轭并除以N(FFT点数)。同时将验证结果xf进行相应的处理,调用np的ifft或者fft。
if IFFT_flag : fft_out = fft_out.conjugate()/N xf = np.fft.ifft(x)else: xf = np.fft.fft(x)最后运行代码,图中蓝线是FFT计算的结果,橙线是FFT库函数计算结果与我们手写代码结果相减的差,差值为0,认为我们的迭代算法正确。
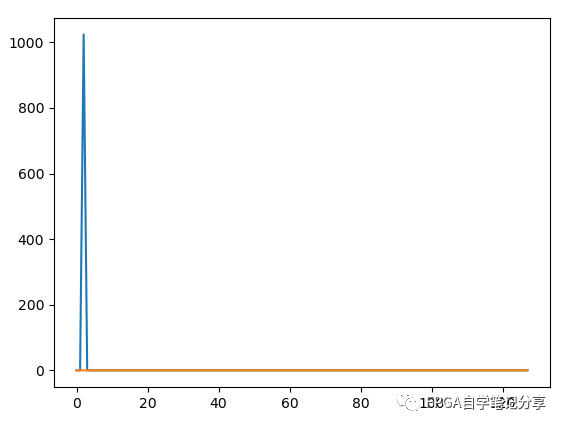
对于verilog代码,IFFT代码的实现更加简单,因为数据求取共轭就是将imag取反即可,修改基2FFT的verilog代码实现及仿真中的代码如下:
首先在输入的位置增加一个判断,IFFT时增加求共轭的操作:
/// ifft 求共轭generate if(C_IFFT_FLAG) begin assign S_data_in_real = I_data_in_real ; assign S_data_in_imag = -I_data_in_imag ; endelse begin assign S_data_in_real = I_data_in_real ; assign S_data_in_imag = I_data_in_imag ; endendgenerate
在输出时,同样增加判断:
generate if(C_IFFT_FLAG) begin assign O_data_out_real = {{3{S_data_out_real[C_DATA_WITH_OUT-1]}},S_data_out_real[C_DATA_WITH_OUT-1:3]} ; assign O_data_out_imag = -{{3{S_data_out_imag[C_DATA_WITH_OUT-1]}},S_data_out_imag[C_DATA_WITH_OUT-1:3]} ; endelse begin assign O_data_out_real = S_data_out_real ; assign O_data_out_imag = S_data_out_imag ; endendgenerate
仿真还是使用python生成数据源送入verilog代码的tb中,比较verilog输出和python输出,最终发现数据两者输出完全相同,IFFT代码实现无误。


 0
0









