前言
上一章讨论了离散贝叶斯滤波器的一些缺点。对于许多跟踪和滤波问题,我们希望有一个单峰和连续的滤波器。例如,我们确定一架飞机的位置在 ( 12.34 , − 95.54 , 2389.5 ) (12.34, -95.54, 2389.5) (12.34,−95.54,2389.5),三个数字分别表示纬度,经度和高度。我们不想让我们的滤波器告诉我们:它可能在 ( 1.65 , − 78.01 , 2100.45 ) (1.65, -78.01, 2100.45) (1.65,−78.01,2100.45),它也可能在 ( 34.36 , − 98.23 , 2543.79 ) (34.36, -98.23, 2543.79) (34.36,−98.23,2543.79)。这与我们的物理直觉不符。
我们希望用一种单峰的、连续的概率来模拟现实世界是如何工作的,并且在计算上是高效的。高斯分布提供了所有这些特征。
均值、方差和标准差
你们大多数人都应该接触过统计数据,但不管怎样,请允许我介绍一下。我要求你阅读这部分内容,即使你确定你很了解。主要有两个原因。首先,我想确定我们使用术语是相同的;第二,我努力让你形成对统计的直观理解。通过学习一门统计课程,只记住公式和计算方式是很容易的,但也许你对所学内容的含义是模糊的。
随机变量
每次掷骰子的结果都在1到6之间,如果我们把一个骰子掷600万次,我们得到1的次数是100万次。因此,我们说结果1的概率是 1 / 6 1/6 1/6。同样地,如果我问你下一次掷骰子的结果是1的概率,你会回答 1 / 6 1/6 1/6。
这种值和对应概率的组合称为随机变量。这里的随机并不意味着过程是不确定的,只是我们缺乏关于结果的信息。掷骰子的结果是确定的,但我们缺乏足够的信息来推算出结果。我们不知道会发生什么,除了概率。
在随机变量的相关理论中,值的范围称为样本空间。对于骰子来说,样本空间是 { 1 , 2 , 3 , 4 , 5 , 6 } \{1, 2, 3, 4, 5, 6\} {1,2,3,4,5,6};对于硬币来说,样本空间是 { H , T } \{H, T\} {H,T}。空间是一个数学术语,意思是数的集合。骰子的样本空间,是自然数的子集(介于1到6之间的自然数)。
另一个随机变量的例子是一所大学里学生的身高,这里的样本空间是生物学定义的两个极限实数之间的范围。
随机变量,如硬币投掷和掷骰子是离散随机变量。这意味着它们的样本空间由有限个值表示的。人类的身高被称为连续随机变量,因为他们可以接受两个极限值之间的任何实际值。
不要混淆随机变量的观测值和实际值。如果我们对一个人身高的观测只能精确到 0.1 m 0.1m 0.1m,那么我们只能记录 0.1 , 0.2 , 0.3 , . . . , 2.7 0.1, 0.2, 0.3, ..., 2.7 0.1,0.2,0.3,...,2.7这些值,产生27个离散的结果。尽管如此,一个人的身高可以在这些范围内的任意实际值之间变化,因此身高是一个连续的随机变量。
在统计学中,大写字母用于表示随机变量,通常来自字母表的后半部分。所以,我们可以说 X X X是代表掷骰子结果的随机变量, Y Y Y是大一学生身高的随机变量。同时,如果我们需要使用到线性代数来解决某些问题,通常遵循的规则是:向量使用小写,矩阵使用大写。不幸的是,这些约定发生冲突,你必须从上下文中确定使用的是哪一个。我总是用粗体符号表示向量和矩阵,这有助于区分两者。
概率分布
概率分布给出了随机变量在样本空间中取任意值的概率。例如,对于一个骰子我们可以说:
| Value | Probability |
|---|---|
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
我们用小写的 p p p表示这个分布: p ( x ) p(x) p(x)。我们可以写:
P ( X = 4 ) = p ( 4 ) = 1 6 P(X = 4) = p (4) = \frac{1}{6} P(X=4)=p(4)=61
这说明骰子的结果是4的概率是1/6。 P ( X = x k ) P(X = x_{k}) P(X=xk)表示随机变量 X X X是 x k x_{k} xk的概率,请注意细微的符号差异。大写 P P P表示单个事件的概率,小写 p p p表示概率分布函数。如果你不善于观察,这可能会使你误入歧途。一些文章使用 P r Pr Pr,而不是 P P P来改善这一点。
另一个例子是硬币,它的样本空间是 { H , T } \{H, T\} {H,T}。硬币是公平的,所以正面(H)的概率是50%,反面(T)的概率是50%。我们把它表示成:
{ P ( X = H ) = 0.5 P ( X = T ) = 0.5 \left\{\begin{matrix} P(X=H) = 0.5 \\ P(X=T) = 0.5 \end{matrix}\right. {P(X=H)=0.5P(X=T)=0.5
样本空间不是唯一的。骰子的一个样本空间是 { 1 , 2 , 3 , 4 , 5 , 6 } \{1, 2, 3, 4, 5, 6\} {1,2,3,4,5,6}。另一个有效的样本空间是 { \{ {偶 , , , 奇 } \} }。一个样本空间,只要它涵盖了所有的可能性,并且任何单个事件只由一个元素描述,那么它就是有效的。 { \{ {偶 , 1 , 3 , 4 , 5 } , 1, 3, 4, 5\} ,1,3,4,5}不是骰子的有效样本空间,因为值4与偶和4都匹配。
离散随机值的所有值的概率称为离散概率分布,连续随机值的所有值的概率称为连续概率分布。
要成为概率分布,每个值 x i x_{i} xi的概率必须 p ( x i ) ≥ 0 p(x_{i}) \ge 0 p(xi)≥0,因为概率不能小于零。其次,所有值的概率之和必须等于1。这对于掷硬币来说应该是直观的:如果得到正面的几率是70%,那么得到反面的几率必须是30%。我们把这个要求公式化为:
对于离散分布:
∑ u P ( X = u ) = 1 \sum_ {u}^{} P(X = u) = 1 u∑P(X=u)=1
对于连续分布:
∫ u P ( X = u ) d u = 1 \int\limits_{u}^{} P(X=u)du = 1 u∫P(X=u)du=1
在上一章中,我们使用概率分布来估计狗在走廊中的位置:
import numpy as np import kf_book.book_plots as book_plots belief = np.array([1, 4, 2, 0, 8, 2, 2, 35, 4, 3, 2]) belief = belief / np.sum(belief) with book_plots.figsize(y=2): book_plots.bar_plot(belief) print('sum = ', np.sum(belief))
sum = 1.0

每个位置的概率都是介于0和1之间,并且所有的概率之和等于1,所以这就是一个概率分布。每个概率都是离散的,所以我们可以更精确地称之为离散概率分布。在实践中,我们经常省略离散和连续这两个字眼,除非我们有特殊的理由作出这种区分。
随机变量的平均值、中位数和峰
给定一组数据,我们通常希望知道该组数据的代表值或均值。对此有很多衡量标准,这个概念被称为集中趋势量度。例如,我们可能想知道一个班级学生的平均身高。我们都知道如何求一组数据的均值,但让我来阐述一下这一点,以便介绍更正式的符号和术语。我们通过求和并除以值的个数来计算均值。如果学生的身高以 m m m为单位:
X = 1.8 , 2.0 , 1.7 , 1.9 , 1.6 X = 1.8,2.0,1.7,1.9,1.6 X=1.8,2.0,1.7,1.9,1.6
我们计算均值为:
μ = 1.8 + 2.0 + 1.7 + 1.9 + 1.6 5 = 1.8 \mu = \frac{1.8 + 2.0 +1.7 + 1.9 + 1.6}{5} = 1.8 μ=51.8+2.0+1.7+1.9+1.6=1.8
传统上,习惯用 μ \mu μ来表示均值。
我们可以把这个计算通用化:
μ = 1 n ∑ i = 1 n x i \mu = \frac{1}{n} \sum_{i = 1}^{n} x_{i} μ=n1i=1∑nxi
NumPy提供numpy.mean()用于计算均值:
x = [1.8, 2.0, 1.7, 1.9, 1.6] np.mean(x)
1.8
为了方便起见,NumPy数组提供mean()方法:
x = np.array([1.8, 2.0, 1.7, 1.9, 1.6]) x.mean()
1.8
一组数字的峰就是最常出现的数字。如果最常出现的数字只有1个,我们就说它是单峰;如果最常出现的数字2个及以上,我们就说它是多峰。例如,集合 { 1 , 2 , 2 , 3 , 4 , 4 } \{1, 2, 2, 3, 4, 4\} {1,2,2,3,4,4}具有2和4两个峰,这是多峰的;集合 { 5 , 7 , 7 , 13 } \{5, 7, 7, 13\} {5,7,7,13}具有7一个峰,因此它是单峰的。在本文中,我们不以这种方式计算峰,而是在更一般的意义上使用了单峰和多峰的概念。例如,我们给狗在不同位置都分配了概率,那么就认为狗的位置是多峰的。
最后,一组数字的中位数就是这组数字排序后的中点。因此,一半的值低于中位数,一半的值高于中位数。如果该组数字的个数是偶数,那么中位数就是这组数字排序后的两个中间数一起求平均值。
Numpy提供numpy.median()来计算中位数。如你所见, { 1.8 , 2.0 , 1.7 , 1.9 , 1.6 } \{1.8, 2.0, 1.7, 1.9, 1.6\} {1.8,2.0,1.7,1.9,1.6}的中位数是1.8,因为1.8是这个集合排序后的第三个元素。在这种情况下,中位数等于平均数,但通常这是不一定的。
np.median(x)
1.8
随机变量的期望值
一个随机变量的期望值是它无穷样本下的均值。即我们取该随机变量的无穷多个样本,然后将这些样本平均在一起。假设 x = [ 1 , 3 , 5 ] x = [1, 3, 5] x=[1,3,5],且每个值的概率相等,那么 x x x的平均值是多少?
当然是 1 , 3 , 5 1, 3, 5 1,3,5的平均值,也就是3。这也是合情合理的:我们期望出现相等数量的1、3和5,所以 ( 1 + 3 + 5 ) / 3 = 3 (1 + 3 + 5) / 3 = 3 (1+3+5)/3=3显然是无限样本的均值。换句话说,这里的期望值是样本空间的均值。
现在假设每个值都有不同的发生概率。假设1有 80 % 80\% 80%的几率发生,3有 15 % 15\% 15%的几率,5只有 5 % 5\% 5%的几率。在这种情况下,我们通过将 x x x的每个值乘以它发生的概率百分比来计算期望值,并对结果求和。对于这种情况,我们可以计算:
E [ X ] = ( 1 ) ( 0.8 ) + ( 3 ) ( 0.15 ) + ( 5 ) ( 0.05 ) = 1.5 \mathbb{E} [X]=(1)(0.8) + (3)(0.15) + (5)(0.05) = 1.5 E[X]=(1)(0.8)+(3)(0.15)+(5)(0.05)=1.5
这里我用符号 E [ X ] \mathbb{E} [X] E[X]表示 x x x的期望值,有些博文使用 E ( x ) E(x) E(x)。 x x x的期望值是1.5也是很直观的,因为 x x x相比较于3或5,更可能是1;相比较于5,更可能是3。
假设 x i x_{i} xi是 x x x的第 i t h i^{th} ith个值, p i p_{i} pi是它发生的概率,那么我们可以用以下公式来形式化期望:
E [ X ] = ∑ i = 1 n p i x i \mathbb{E}[X] = \sum_{i = 1}^{n}p_{i}x_{i} E[X]=i=1∑npixi
一点点代数知识表明,如果如果所有数出现的概率都相等,则期望值与平均值相同:
E [ X ] = ∑ i = 1 n p i x i = 1 n ∑ i = 1 n x i = μ x \mathbb{E}[X] = \sum_{i = 1}^{n}p_{i}x_{i} = \frac{1}{n} \sum_{i = 1}^{n}x_{i} = \mu _{x} E[X]=i=1∑npixi=n1i=1∑nxi=μx
如果 x x x是连续的,我们用积分来代替求和,就像这样:
E [ X ] = ∫ a b x f ( x ) d x \mathbb{E}[X] = \int_{a}^{b}xf(x)dx E[X]=∫abxf(x)dx
其中, f ( x ) f(x) f(x)是 x x x的概率分布函数。
我们可以编写一点Python来模拟这一点。这里我取1000000个样本,计算我们刚刚分析计算的分布的期望值:
total = 0 N = 1000000 for r in np.random.rand(N): if r <= .80: total += 1 elif r < .95: total += 3 else: total += 5 total / N
1.49924
你可以看到,计算出的值很接近分析求解出的值。这是因为计算出的值并不精确,如果想要获得精确的值需要无限的样本大小。
练习
骰子的期望值是多少?
解决方法
骰子每一面的概率都是相等的,所以每一面的概率都是 1 / 6 1/6 1/6。因此:
E [ X ] = 1 / 6 × 1 + 1 / 6 × 2 + 1 / 6 × 3 + 1 / 6 × 4 + 1 / 6 × 5 + 1 / 6 × 6 = 3.5 \mathbb{E}[X] = 1/6 \times 1 + 1/6 \times 2 + 1/6 \times 3 + 1/6 \times 4 + 1/6 \times 5 + 1/6 \times 6 = 3.5 E[X]=1/6×1+1/6×2+1/6×3+1/6×4+1/6×5+1/6×6=3.5
练习
给定均匀连续分布,计算 a = 0 a=0 a=0和 b = 20 b=20 b=20的期望值:
f ( x ) = 1 b − a f(x) = \frac{1}{b-a} f(x)=b−a1
解决方法
E [ X ] = ∫ 0 20 x 1 20 d x = [ x 2 40 ] 0 20 = 10 − 0 = 10 \mathbb{E}[X] = \int_{0}^{20}x\frac{1}{20}dx=\left [ \frac{x^{2}}{40} \right ] _{0}^{20} = 10-0 = 10 E[X]=∫020x201dx=[40x2]020=10−0=10
随机变量的方差
上面的计算告诉我们学生的平均身高,但它并不能告诉我们我们想知道的一切。例如,假设我们有三个班级的学生,我们给他们贴上 X X X、 Y Y Y和 Z Z Z的标签,身高数据如下:
X = [1.8, 2.0, 1.7, 1.9, 1.6] Y = [2.2, 1.5, 2.3, 1.7, 1.3] Z = [1.8, 1.8, 1.8, 1.8, 1.8]
使用NumPy,我们看到每个班级的平均高度是相同的。
print(np.mean(X), np.mean(Y), np.mean(Z))
1.8 1.8 1.8
每个班级的平均高度都是 1.8 m 1.8m 1.8m,但请注意,第二个班级的身高变化比第一个班级大得多,而第三个班级的身高变化则完全没有。
均值告诉我们数据的部分信息,但不是全部,我们希望能够具体说明学生身高之间的差异有多大。你可以想象到有很多原因,也许一个学区需要订购5000张课桌,而且他们希望购买的课桌尺寸能适应学生的身高范围。
统计学把样本之间差异的概念形式化为标准差和方差。计算方差的公式是:
V A R ( X ) = E [ ( X − μ ) 2 ] VAR(X) = \mathbb{E} \left [ (X - \mu )^{2} \right ] VAR(X)=E[(X−μ)2]
暂时忽略平方,可以看到方差是样本空间 X X X与平均值 μ \mu μ的变化量的期望值: ( X − μ ) (X-\mu ) (X−μ),我稍后将解释平方项的用途。
期望值的公式是 E [ X ] = ∑ i = 1 n p i x i \mathbb{E}[X] = \sum _{i=1}^{n}p_{i}x_{i} E[X]=∑i=1npixi,因此我们可以将其代入上面的等式中得到:
V A R ( X ) = 1 n ∑ i = 1 n ( x i − μ ) 2 VAR(X) = \frac{1}{n} \sum _{i=1}^{n} (x_{i} - \mu )^{2} VAR(X)=n1i=1∑n(xi−μ)2
让我们计算三个班级的方差,看看我们得到了什么值,并熟悉这个概念。
X X X的平均值是1.8( μ x = 1.8 \mu _{x} = 1.8 μx=1.8),所以我们得到:
V A R ( X ) = ( 1.8 − 1.8 ) 2 + ( 2 − 1.8 ) 2 + ( 1.7 − 1.8 ) 2 + ( 1.9 − 1.8 ) 2 + ( 1.6 − 1.8 ) 2 5 = 0.02 m 2 VAR(X) = \frac{(1.8-1.8)^{2} + (2-1.8)^{2} + (1.7-1.8)^{2} + (1.9-1.8)^{2} + (1.6-1.8)^{2}}{5} = 0.02m^{2} VAR(X)=5(1.8−1.8)2+(2−1.8)2+(1.7−1.8)2+(1.9−1.8)2+(1.6−1.8)2=0.02m2
NumPy提供函数var()来计算方差:
print("{:.2f} meters squared".format(np.var(X)))
0.02 meters squared
这也许有点难以解释。高度以 m m m为单位,但方差是 m 2 m^{2} m2。因此,我们有一个更常用的度量,标准差,它被定义为方差的平方根:
σ = V A R ( X ) = 1 n ∑ i = 1 n ( x i − μ ) 2 \sigma = \sqrt[]{VAR(X)} = \sqrt[]{\frac{1}{n} \sum _{i=1}^{n} (x_{i} - \mu )^{2} } σ=VAR(X)=n1i=1∑n(xi−μ)2
标准差通常表示为 σ \sigma σ,方差通常表示为 σ 2 \sigma ^{2} σ2。
对于第一个班级,我们可以得到:
σ x = ( 1.8 − 1.8 ) 2 + ( 2 − 1.8 ) 2 + ( 1.7 − 1.8 ) 2 + ( 1.9 − 1.8 ) 2 + ( 1.6 − 1.8 ) 2 5 = 0.1414 m \sigma _{x} = \sqrt[]{\frac{(1.8-1.8)^{2} + (2-1.8)^{2} + (1.7-1.8)^{2} + (1.9-1.8)^{2} + (1.6-1.8)^{2}}{5}} = 0.1414m σx=5(1.8−1.8)2+(2−1.8)2+(1.7−1.8)2+(1.9−1.8)2+(1.6−1.8)2=0.1414m
我们可以用NumPy的numpy.std()方法来计算标准差,std是标准差的常用缩写。
print('std {:.4f}'.format(np.std(X))) print('var {:.4f}'.format(np.std(X)**2))
std 0.1414 var 0.0200
标准差意味着什么?它告诉我们高度之间的差异有多少。在很多情况下, 68 % 68\% 68%的值都在均值的一个标准差之内。换言之,我们可以得出结论,对于随机一个班级班, 68 % 68\% 68%的学生身高在1.66( 1.8 − 0.1414 1.8 - 0.1414 1.8−0.1414)到1.94( 1.8 + 0.1414 1.8 + 0.1414 1.8+0.1414)之间。
我们可以在绘图中查看:
from kf_book.gaussian_internal import plot_height_std import matplotlib.pyplot as plt plot_height_std(X)

对于只有5个学生,我们显然不会在一个标准差内得到准确的 68 % 68\% 68%。从图像中可以看到,5个学生中有3个在 ± 1 σ \pm 1\sigma ±1σ范围内,即 60 % 60\% 60%。仅用5个样本就能达到的比例与 68 % 68\% 68%非常接近。让我们看一个有100名学生的班级的结果。
from numpy.random import randn data = 1.8 + randn(100)*.1414 mean, std = data.mean(), data.std() plot_height_std(data, lw=2) print(f'mean = {mean:.3f}') print(f'std = {std:.3f}')
mean = 1.811 std = 0.130

肉眼观察,大约 68 % 68\% 68%的高度在平均值1.8的 ± 1 σ \pm 1\sigma ±1σ范围内,但我们可以用代码验证这一点。
np.sum((data > mean-std) & (data < mean+std)) / len(data) * 100.
69.0
我们很快会更深入地讨论这个问题。现在让我们来计算
Y = [ 2.2 , 1.5 , 2.3 , 1.7 , 1.3 ] Y = [2.2, 1.5, 2.3, 1.7, 1.3] Y=[2.2,1.5,2.3,1.7,1.3]
Y Y Y的平均值为 μ = 1.8 \mu = 1.8 μ=1.8,所以
σ y = ( 2.2 − 1.8 ) 2 + ( 1.5 − 1.8 ) 2 + ( 2.3 − 1.8 ) 2 + ( 1.7 − 1.8 ) 2 + ( 1.3 − 1.8 ) 2 5 = 0.39 m \sigma _{y} = \sqrt[]{\frac{(2.2-1.8)^{2} + (1.5-1.8)^{2} + (2.3-1.8)^{2} + (1.7-1.8)^{2} + (1.3-1.8)^{2}}{5}} = 0.39m σy=5(2.2−1.8)2+(1.5−1.8)2+(2.3−1.8)2+(1.7−1.8)2+(1.3−1.8)2=0.39m
我们可以用NumPy确认:
print('std of Y is {:.2f} m'.format(np.std(Y)))
std of Y is 0.39 m
这符合我们的预期。 Y Y Y的高度变化较大,标准差较大。
最后,让我们计算 Z Z Z的标准差。由于数值没有变化,所以我们希望标准偏差为零。
σ z = ( 1.8 − 1.8 ) 2 + ( 1.8 − 1.8 ) 2 + ( 1.8 − 1.8 ) 2 + ( 1.8 − 1.8 ) 2 + ( 1.8 − 1.8 ) 2 5 = 0 m \sigma _{z} = \sqrt[]{\frac{(1.8-1.8)^{2} + (1.8-1.8)^{2} + (1.8-1.8)^{2} + (1.8-1.8)^{2} + (1.8-1.8)^{2}}{5}} = 0m σz=5(1.8−1.8)2+(1.8−1.8)2+(1.8−1.8)2+(1.8−1.8)2+(1.8−1.8)2=0m
print(np.std(Z))
0.0
在我们继续之前,需要指出的是,我忽略了一点:男人的平均身高比女人高。一般来说,一个只有男性或女性的班级的身高差异会小于一个男女都有的班级。其他因素也是如此:营养良好的孩子比营养不良的孩子高等。统计学家在设计实验时需要考虑这些因素。
我建议我们为学校订购课桌时,可以进行这种分析。对于每个年龄组,可能有两种不同的方法——一种聚集在女性的平均身高周围,另一种聚集在男性的平均身高周围,而整个班级的平均数将介于两者之间。如果我们按照所有学生的平均身高购买课桌,我们很可能会得到既不适合男生也不适合女生的课桌!
为什么是差异的平方
为什么计算方差,我们使用的是差异的平方?我可以用很多数学知识探讨,但让我们用一种简单的方式来看待这个问题。这是一张 X = [ 3 , − 3 , 3 , − 3 ] X = [3, −3, 3, −3] X=[3,−3,3,−3]值的图表:
X = [3, -3, 3, -3] mean = np.average(X) for i in range(len(X)): plt.plot([i ,i], [mean, X[i]], color='k') plt.axhline(mean) plt.xlim(-1, len(X)) plt.tick_params(axis='x', labelbottom=False)

np.mean()和np.average()都是计算均值的函数,在不指定权重的时候average()和mean()是一样的。指定权重后,average可以计算加权均值。
如果我们不考虑差异的平方,这些符号会抵消一切:
( 3 − 0 ) + ( − 3 − 0 ) + ( 3 − 0 ) + ( − 3 − 0 ) 4 = 0 \frac{(3-0)+(-3-0)+(3-0)+(-3-0)}{4} = 0 4(3−0)+(−3−0)+(3−0)+(−3−0)=0
这显然是不正确的,因为数据中的方差大于0。
也许我们可以用绝对值?通过检查我们可以看出,结果是 12 / 4 = 3 12/4 = 3 12/4=3,这当然是正确的——每个值都与平均值相差3。但是如果我们有 Y = [ 6 , − 2 , − 3 , 1 ] Y=[6, −2, −3, 1] Y=[6,−2,−3,1],怎么办?在这种情况下,我们得到 12 / 4 = 3 12/4 = 3 12/4=3。 Y Y Y显然比 X X X更分散,但计算得到的方差相同。如果我们使用平方的公式,我们得到 Y Y Y的方差为3.5,这反映了它更大的方差。
这不是正确的证明,事实上,这项技术的发明者Carl Friedrich Gauss认识到这有点武断。如果存在异常值,则平方差会给该项带来不成比例的权重。例如,让我们看看如果我们有:
X = [1, -1, 1, -2, -1, 2, 1, 2, -1, 1, -1, 2, 1, -2, 100] print(f'Variance of X with outlier = {np.var(X):6.2f}') print(f'Variance of X without outlier = {np.var(X[:-1]):6.2f}')
Variance of X with outlier = 621.45 Variance of X without outlier = 2.03
你告诉我,这个对吗?如果没有异常值100,我们得到 σ 2 = 2.03 \sigma^{2} = 2.03 σ2=2.03,这准确地反映了在没有异常值的情况下 X X X是如何变化的。然而,一个异常值淹没了整个方差的计算。我们是想淹没计算,使我们知道有一个异常值;还是强有力地剔除异常值,但仍然提供一个剩下正常值的方差?显然,这取决于你要解决的问题。
高斯
我们现在准备学习高斯,让我们回顾下学习本文的动机。
我们希望用一种单峰的、连续的方式来表示概率,以模拟现实世界是如何工作的,并且希望它的计算是高效的。
让我们看一张高斯分布图,来了解一下我们在说什么。
from filterpy.stats import plot_gaussian_pdf plot_gaussian_pdf(mean=1.8, variance=0.1414**2, xlabel='Student Height', ylabel='pdf')

这个曲线是概率密度函数,简称pdf,它显示了随机变量取值的相对可能性。从图表中我们可以看出,学生身高接近 1.8 m 1.8m 1.8m的可能性比 1.7 m 1.7m 1.7m的可能性要大得多, 1.9 m 1.9m 1.9m的可能性比 1.4 m 1.4m 1.4m的可能性要大得多。换句话说,许多学生身高接近 1.8 m 1.8m 1.8m,只有极少数学生身高达到 1.4 m 1.4m 1.4m或 2.2 m 2.2m 2.2m。最后请注意,曲线以均值 1.8 m 1.8m 1.8m左右对称。
高斯分布是普遍存在的,因为在现实世界中,许多观测值是以这种钟形曲线的方式存在的。因此,也有人会用钟形曲线来表示高斯分布。但我不会,因为还有许多的概率分布也具有相似的钟形曲线形状。
这条曲线并不是学生身高所独有的——大量的自然现象都表现出这种分布,包括我们用于滤波问题的传感器。正如我们将看到的,它具有我们正在寻找的所有属性——单峰、连续、计算效率高。而且,它还有其他我们可能没有意识到的良好性质。
回忆离散贝叶斯一文中概率分布的形状:
import kf_book.book_plots as book_plots belief = [0., 0., 0., 0.1, 0.15, 0.5, 0.2, .15, 0, 0] book_plots.bar_plot(belief)

它不是完美的高斯曲线,但它们是相似的。我们可以用高斯来代替那里使用的离散概率!
术语
在我们继续之前,先来点术语——下图描述了一个随机变量的值在 ( − ∞ , + ∞ ) (-\infty , +\infty ) (−∞,+∞)之间的概率密度。这是什么意思?想象一下,我们在高速公路上对正在行驶的汽车的速度进行观测,那我们就可以将不同速度下的汽车的占比绘制出来。如果平均速度为 120 h m / h 120hm/h 120hm/h,则可能如下所示:
plot_gaussian_pdf(mean=120, variance=17**2, xlabel='speed(kph)')

y y y轴描绘了概率密度——以对应 x x x轴上的速度行驶的车辆的对应值。
高斯模型也并不是完美的。虽然图表没有完全显示,但分布的尾部延伸到无穷远。尾部是曲线的远端,其值最低。当然,人的身高或汽车的速度不能小于零,更不用说 − ∞ -\infty −∞或 + ∞ +\infty +∞。高斯分布模拟了实测车速的分布,但作为一个模型,它显然是不完美的。模型和现实之间的差异,将在滤波器中反复出现。高斯分布在数学的许多分支中都有应用,并不是因为它们完美地模拟了现实,而是因为它们比任何其他相对精确的选择都更易于计算和使用。
你会听到高斯分布,也被称为正态分布。高斯函数和正态函数在本文中的含义相同,可以互换使用,我希望你习惯于看到这两个。
高斯分布
让我们来探索高斯函数是如何工作的。高斯分布是一个连续的概率分布,它完全由两个参数描述,均值( μ \mu μ)和方差( σ 2 \sigma ^{2} σ2)。它定义为:
f ( x , μ , σ ) = 1 σ 2 π e x p [ − ( x − μ ) 2 2 σ 2 ] f(x, \mu ,\sigma ) = \frac{1}{\sigma \sqrt[]{2\pi } } exp[-\frac{(x-\mu )^{2}}{2\sigma ^{2}} ] f(x,μ,σ)=σ2π1exp[−2σ2(x−μ)2]
其中, e x p [ x ] exp[x] exp[x]是 e x e^{x} ex的符号缩写。
如果你以前没见过这个方程式,就不要被它所劝阻,你不需要记忆它。此函数的计算存储在stats.py的gaussian(x, mean, var, normed=True)函数。
去掉常数,你可以看到它是一个简单的指数:
f ( x ) ∝ e − x 2 f(x) \propto e^{-x^{2}} f(x)∝e−x2
它有我们熟悉的钟形曲线形状:
x = np.arange(-3, 3, .01) plt.plot(x, np.exp(-x**2))

让我们绘制一个平均值为22( μ = 22 \mu =22 μ=22)、方差为4( σ 2 = 4 \sigma ^{2}=4 σ2=4)的高斯曲线。
plot_gaussian_pdf(22, 4, mean_line=True, xlabel='$^{\circ}C$')

这个曲线是什么意思?假设我们有一个读数为 22 ° C 22°C 22°C的温度计,没有一个温度计是完全准确的,因此我们的每个读数都会稍微偏离实际值。然而,中心极限定理指出,如果我们进行多次观测,观测值将是正态分布的。当我们看这个图表时,我们可以看到它与温度计在 22 ° C 22°C 22°C的实际温度下读取特定值的概率成正比。
回想一下高斯分布是连续的。想象一条无限长的直线——你随机选取的一个位于2的点的概率是多少。显然是 0 % 0\% 0%,因为有无数的选择可供选择。正态分布也是如此;在上图中,恰好为 22 ° C 22°C 22°C的概率为 0 % 0\% 0%,因为读数可以取无穷多的值。
这个曲线是什么?我们称之为概率密度函数。曲线下任意区域的面积给出概率。例如,如果你计算 20 ° C 20°C 20°C到 22 ° C 22°C 22°C之间曲线下的面积,得到的面积就是温度读数在这两个温度之间的概率。
还有另一种理解它的方法。岩石或海绵的密度是多少?密度是一种度量给定空间大小的的质量的方法。岩石密度较大,海绵较小。所以,如果你想知道一块岩石有多重但没有直接观测出重量的仪器,你可以取它的体积乘以它的密度。实际上,大多数对象的密度都是不均匀的,因此可以将岩石体积的局部密度进行积分。
M = ∫ ∫ ∫ R p ( x , y , z ) d V M=\int \int \int_{R}^{} p(x, y, z) dV M=∫∫∫Rp(x,y,z)dV
我们对概率密度也是这样。如果你想知道温度在 20 ° C 20°C 20°C到 21 ° C 21°C 21°C之间的可能性,你可以把上面的曲线从20到21积分。如你所知,曲线的积分给出了曲线下的面积。因为这是概率密度的曲线,所以密度的积分就是概率。
上面说到,一个点的概率是 0 % 0\% 0%。实际上,我们的传感器没有无限精度。因此, 22 ° C 22°C 22°C的读数意味着一个范围,例如 22 ± 0.1 ° C 22\pm 0.1°C 22±0.1°C,我们可以通过从 21.9 ° C 21.9°C 21.9°C到 22.1 ° C 22.1°C 22.1°C的积分来计算该范围的概率。
你怎么计算概率,或者曲线下的面积?积分高斯函数的方程:
∫ x 0 x 1 1 σ 2 π e − ( x − μ ) 2 2 σ 2 d x \int_{x_{0}}^{x_{1}} \frac{1}{\sigma \sqrt[]{2\pi } } e^{-\frac{(x-\mu )^{2}}{2\sigma ^{2}} } dx ∫x0x1σ2π1e−2σ2(x−μ)2dx
这被称为累积概率分布,通常缩写为cdf。
filterpy.stats.norm_cdf为你计算了积分的结果。例如,我们可以计算:
from filterpy.stats import norm_cdf print('Cumulative probability of range 21.5 to 22.5 is {:.2f}%'.format( norm_cdf((21.5, 22.5), 22,4)*100)) print('Cumulative probability of range 23.5 to 24.5 is {:.2f}%'.format( norm_cdf((23.5, 24.5), 22,4)*100))
Cumulative probability of range 21.5 to 22.5 is 19.74% Cumulative probability of range 23.5 to 24.5 is 12.10%
平均值( μ \mu μ)就是它听起来的样子——所有可能的均值。由于曲线的对称形状,它也是曲线最高部分的 x x x的取值。温度计的读数是 22 ° C 22°C 22°C,所以这就是我们计算的均值。
随机变量 X X X的正态分布的表示法是 X ∼ N ( μ , σ 2 ) X\sim N(\mu , \sigma ^{2}) X∼N(μ,σ2)。其中, ∼ \sim ∼表示服从的分布。这意味着我可以把温度计的温度读数表示为:
t e m p ∼ N ( 22 , 4 ) temp\sim N(22, 4) temp∼N(22,4)
这是一个极其重要的结果。高斯函数允许我用两个数,来捕捉无穷多的可能值!利用 μ = 22 \mu = 22 μ=22和 σ 2 = 4 \sigma ^{2} = 4 σ2=4,我可以计算任何范围内的观测分布。
方差
因为这是一个概率密度分布,所以要求曲线下的面积总是等于1。这应该是直观清晰的——曲线下的区域代表所有可能的结果,发生了一些事情,而发生一些事情的概率是1,所以密度总和必须是1。我们可以用一些代码来证明这一点(如果你在数学上将高斯方程从 − ∞ -\infty −∞积分到 + ∞ +\infty +∞)。
print(norm_cdf((-1e8, 1e8), mu=0, var=4))
1.0
这就引出了一个重要的结论:如果方差很小,曲线就会很窄。这是因为方差是衡量样本与均值之间差异的一个指标。要使面积等于1,曲线也必须很高;另一方面,如果方差很大,曲线就会很宽,因此它也必须很低,使面积等于1。
让我们从图形上看一下,我们可以通过filterpy.stats.gaussian()看看这个现象(采用单个值或值数组)。
from filterpy.stats import gaussian print(gaussian(x=3.0, mean=2.0, var=1)) print(gaussian(x=[3.0, 2.0], mean=2.0, var=1))
0.24197072451914337 [0.378 0.622]
默认情况下,高斯函数将输出标准化,从而将输出变回概率分布。使用参数normed来控制这个。
print(gaussian(x=[3.0, 2.0], mean=2.0, var=1, normed=False))
[0.242 0.399]
如果高斯分布不是标准化的,它被称为高斯函数而不是高斯分布。
xs = np.arange(15, 30, 0.05) plt.plot(xs, gaussian(xs, 23, 0.2**2), label='$\sigma^2=0.2^2$') plt.plot(xs, gaussian(xs, 23, .5**2), label='$\sigma^2=0.5^2$', ls=':') plt.plot(xs, gaussian(xs, 23, 1**2), label='$\sigma^2=1^2$', ls='--') plt.legend()

这告诉我们什么? σ 2 = 0. 2 2 \sigma ^{2} = 0.2^{2} σ2=0.22的高斯分布非常窄。这是说,我们非常相信 x = 23 x=23 x=23。相比之下, σ 2 = 1 2 \sigma ^{2} = 1^{2} σ2=12的高斯分布也相信 x = 23 x=23 x=23,但我们此时就不太确定了。我们认为 x = 23 x=23 x=23变低了,因此我们对 X X X可能值的看法是分散的——例如,我们认为 x = 20 x=20 x=20或 x = 26 x=26 x=26也都是蛮有可能的。 σ 2 = 0. 2 2 \sigma ^{2} = 0.2^{2} σ2=0.22几乎完全消除了22或24作为可能值,而 σ 2 = 1 2 \sigma ^{2} = 1^{2} σ2=12认为它们几乎与23差不多,只略低一些。
如果我们回想一下温度计,我们可以认为这三条曲线代表了三个不同温度计的读数。 σ 2 = 0. 2 2 \sigma ^{2} = 0.2^{2} σ2=0.22的曲线表示非常准确的温度计, σ 2 = 1 2 \sigma ^{2} = 1^{2} σ2=12的曲线表示相当不准确的温度计。注意高斯分布给我们的非常强大的属性——我们可以完全用两个数字来表示温度计的读数和误差,即均值和方差。
高斯函数的等效形式是 N ( μ , 1 / τ ) N(\mu , 1/\tau) N(μ,1/τ),其中 μ \mu μ是平均值, τ \tau τ是精度。 1 / τ = σ 2 1/\tau = \sigma ^{2} 1/τ=σ2,它是方差的倒数。虽然我们在本文中并没有使用这个公式,但它强调了方差是衡量我们的数据有多精确的一个指标。一个小的方差产生大的精度,表示我们的观测是非常精确的;相反,一个大的方差产生低精度:我们的观测可能没有那么精确了。你应该习惯于用这些等价形式来考虑高斯。
68-95-99.7规则
现在花点时间讨论标准差是值得的,标准差是衡量数据偏离均值的程度。对于高斯分布, 68 % 68\% 68%的数据落在均值的一个标准差( ± 1 σ \pm 1\sigma ±1σ)内, 95 % 95\% 95%落在两个标准差( ± 2 σ \pm 2\sigma ±2σ)内, 99.7 % 99.7\% 99.7%落在三个标准差( ± 3 σ \pm 3\sigma ±3σ)内。这通常被称为68-95-99.7规则。
如果你被告知一个班级的平均考试成绩是71分,标准差是9.4,你可以得出结论:如果分布是正态分布, 95 % 95\% 95%的学生得到的分数在52.2到89.8之间,即用 71 ± ( 2 × 9.4 ) 71\pm (2\times 9.4) 71±(2×9.4)计算。
最后,注意一下单位。如果我们位置的高斯分布是 μ = 22 m \mu = 22m μ=22m,那么标准差的单位也是 m m m。因此, σ = 0.2 \sigma = 0.2 σ=0.2意味着 68 % 68\% 68%的观测范围在 21.8 m 21.8m 21.8m到 22.2 m 22.2m 22.2m之间。方差是标准差的平方,因此 σ 2 = 0.04 m 2 \sigma^{2} = 0.04m^{2} σ2=0.04m2。正如你在上文的一些表述中所看到的,写 σ 2 = 0. 2 2 \sigma^{2} = 0.2^{2} σ2=0.22很有意义,因为0.2与数据的单位相同。
下图描述了标准差和正态分布之间的关系。
from kf_book.gaussian_internal import display_stddev_plot display_stddev_plot()

交互动图
对于那些在Jupyter笔记本上读到这篇文章的人来说,这里是高斯的交互动图。使用滑块修改 μ \mu μ和 σ 2 \sigma ^{2} σ2。调整 μ \mu μ将使图形左右移动,而调整 σ 2 \sigma ^{2} σ2将使钟形曲线改变宽窄情况。
import math from ipywidgets import interact, FloatSlider def plt_g(mu,variance): plt.figure() xs = np.arange(2, 8, 0.01) ys = gaussian(xs, mu, variance) plt.plot(xs, ys) plt.ylim(0, 0.04) interact(plt_g, mu=FloatSlider(value=5, min=3, max=7), variance=FloatSlider(value = .03, min=.01, max=1.))
如果你没有本地运行环境,可以点击链接在线运行调试(加载的时间可能比较久):http://mybinder.org/repo/rlabbe/Kalman-and-Bayesian-Filters-in-Python
最后,如果你在网上阅读这篇文章,这里有一个高斯函数的动图。首先,均值右移。然后平均值以 μ = 5 \mu = 5 μ=5为中心,修改方差。

高斯函数的计算性质
离散贝叶斯滤波器的工作原理是将任意概率分布相乘和相加。卡尔曼滤波器使用高斯分布代替任意分布,但其余的算法几乎保持不变。这意味着我们将需要乘和加高斯。
高斯分布的一个显著特性是两个独立高斯的和是另一个高斯分布!乘积不是高斯的,而是与高斯成比例的。在这里我们可以说两个高斯分布相乘的结果是一个高斯函数(在这种情况下,高斯函数而不是高斯分布,意味着不能保证概率密度值和为1的性质)。
在我们做数学推导之前,让我们直观地测试一下。
x = np.arange(-1, 3, 0.01) g1 = gaussian(x, mean=0.8, var=.1) g2 = gaussian(x, mean=1.3, var=.2) plt.plot(x, g1, x, g2) g = g1 * g2 # element-wise multiplication g = g / sum(g) # normalize plt.plot(x, g, ls='-.')

在这里,我创建了两个高斯, g 1 = N ( 0.8 , 0.1 ) g1=N(0.8, 0.1) g1=N(0.8,0.1)和 g 2 = N ( 1.3 , 0.2 ) g2=N(1.3, 0.2) g2=N(1.3,0.2),并绘制了它们。然后我将它们相乘,并将结果归一化。如你所见,结果看起来像是高斯分布。
高斯函数是非线性函数。通常情况下,如果你把两个非线性方程相乘,你会得到一个不同类型的函数。例如,两个 s i n sin sin相乘的形状与 s i n ( x ) sin(x) sin(x)非常不同。
x = np.arange(0, 4*np.pi, 0.01) plt.plot(np.sin(1.2*x)) plt.plot(np.sin(1.2*x) * np.sin(2*x))

但是两个高斯分布相乘的结果是一个高斯函数。这是卡尔曼滤波器在计算上可行的一个关键原因。换句话说,卡尔曼滤波器使用高斯函数,因为它们在计算上表现很好。
两个独立高斯的乘积,由下式给出:
μ = σ 1 2 μ 2 + σ 2 2 μ 1 σ 1 2 + σ 2 2 \mu = \frac{\sigma _{1}^{2}\mu _{2} + \sigma _{2}^{2}\mu _{1}}{\sigma _{1}^{2} + \sigma _{2}^{2}} μ=σ12+σ22σ12μ2+σ22μ1
σ 2 = σ 1 2 σ 2 2 σ 1 2 + σ 2 2 \sigma ^{2} = \frac{\sigma _{1}^{2}\sigma _{2}^{2}}{\sigma _{1}^{2} + \sigma _{2}^{2}} σ2=σ12+σ22σ12σ22
两个独立高斯的和,由下式给出:
μ = μ 1 + μ 2 \mu = \mu _{1} + \mu _{2} μ=μ1+μ2
σ 2 = σ 1 2 + σ 2 2 \sigma ^{2} = \sigma _{1}^{2} + \sigma _{2}^{2} σ2=σ12+σ22
在本文的结尾,我推导了这些方程。然而,理解这个计算过程并不是很重要。
高斯联系滤波
现在我们讨论使用高斯如何用于滤波。在下一篇文章中,我们将使用高斯实现一个滤波器。这里我将解释为什么我们要使用高斯。
在上一章中,我们用数组表示概率分布。我们通过计算,该分布与另一个表示观测似然的分布相乘来执行更新计算,如下所示:
def normalize(p): return p / sum(p) def update(likelihood, prior): return normalize(likelihood * prior) prior = normalize(np.array([4, 2, 0, 7, 2, 12, 35, 20, 3, 2])) likelihood = normalize(np.array([3, 4, 1, 4, 2, 38, 20, 18, 1, 16])) posterior = update(likelihood, prior) book_plots.bar_plot(posterior)

换句话说,我们必须计算10次乘法才能得到这个结果。对于具有多维大数组的真实滤波器,我们需要数十亿次乘法和大量内存。
但是这个分布看起来很像高斯分布。如果我们用高斯函数代替数组呢?我将计算后验值的均值和方差,并将其绘制在条形图上:
xs = np.arange(0, 10, .01) def mean_var(p): x = np.arange(len(p)) mean = np.sum(p * x,dtype=float) var = np.sum((x - mean)**2 * p) return mean, var mean, var = mean_var(posterior) book_plots.bar_plot(posterior) plt.plot(xs, gaussian(xs, mean, var, normed=False), c='r') print('mean: %.2f' % mean, 'var: %.2f' % var)
mean: 5.88 var: 1.24

这令人印象深刻。我们可以用两个数字来描述一个完整的分布。也许这个例子是没有说服力的,因为在分布中只有10个数字。但一个真正的问题可能有数百万个数字,但使用高斯仍然只需要两个数字来描述它。
回想一下我们的滤波器用的更新函数:
def update(likelihood, prior): return normalize(likelihood * prior)
如果数组包含一百万个元素,那就是一百万次乘法。但是,如果我们用高斯函数代替数组,那么我们将用:
μ = σ 1 2 μ 2 + σ 2 2 μ 1 σ 1 2 + σ 2 2 \mu = \frac{\sigma _{1}^{2}\mu _{2} + \sigma _{2}^{2}\mu _{1}}{\sigma _{1}^{2} + \sigma _{2}^{2}} μ=σ12+σ22σ12μ2+σ22μ1
σ 2 = σ 1 2 σ 2 2 σ 1 2 + σ 2 2 \sigma ^{2} = \frac{\sigma _{1}^{2}\sigma _{2}^{2}}{\sigma _{1}^{2} + \sigma _{2}^{2}} σ2=σ12+σ22σ12σ22
整个流程只有三次乘法,二次除法。
贝叶斯理论
在上一篇文章中,我们通过推理我们在每一时刻所拥有的信息开发了一个算法,我们将其表示为离散概率分布。在这个过程中我们发现了贝叶斯定理。贝叶斯定理告诉我们,如何在给定先验的情况下计算事件发生的概率。
我们使用以下概率公式来实现update()函数:
p o s t e r i o r = l i k e l i h o o d × p r i o r n o r m a l i z a t i o n posterior = \frac{likelihood \times prior}{normalization} posterior=normalizationlikelihood×prior
这实际上就是贝叶斯定理,但在许多方面,这掩盖了这个方程最简单的想法。我们将此解读为:
u p d a t e d k n o w l e d g e = ∣ l i k e l i h o o d o f n e w k n o w l e d g e × p r i o r k n o w l e d g e ∣ updated\ knowledge= \left | likelihood\ of\ new\ knowledge \times prior\ knowledge \right | updated knowledge=∣likelihood of new knowledge×prior knowledge∣
其中, ∣ ⋅ ∣ \left | \cdot \right | ∣⋅∣表示归一化。
回顾一下,先验是在我们包含观测信息之前事情发生的概率,后验是我们在包含观测的信息之后事情发生的概率。
贝叶斯定理是:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
P ( A ∣ B ) P(A|B) P(A∣B)称为条件概率。也就是说,它表示如果B发生的情况下,A发生的概率。例如,如果昨天下雨的话,今天下雨的可能性要比昨天是晴天的可能性大,因为降雨系统通常持续一天以上。考虑到昨天下雨,我们把今天下雨的概率写成 P ( P( P(今天下雨 ∣ | ∣昨天下雨 ) ) )。
这忽略了一个重要的问题。在很多时候,我们使用的不是单一的概率,而是一组概率——概率分布。我刚才给贝叶斯方程使用的是概率,而不是概率分布。然而,它同样适用于概率分布。我们对概率分布使用小写的 p p p:
p ( A ∣ B ) = p ( B ∣ A ) p ( A ) p ( B ) p(A|B) = \frac{p(B|A)p(A)}{p(B)} p(A∣B)=p(B)p(B∣A)p(A)
在上面的等式中, B B B是证据, P ( A ) P(A) P(A)是先验, P ( B ∣ A ) P(B|A) P(B∣A)是似然, P ( A ∣ B ) P(A|B) P(A∣B)是后验。根据公式,我们可以看出贝叶斯定理与update()函数的匹配度:我们将使用 x i x_{i} xi作为 i i i时刻的位置,观测值是 z z z。因此,我们想知道 P ( x i ∣ z ) P(x_{i}| z) P(xi∣z),也就是说,给定观测值 z z z,狗在 x i x_{i} xi的概率。
那么,让我们把它代入方程,然后求解它:
P ( x i ∣ z ) = P ( z ∣ x i ) P ( x i ) P ( z ) P(x_{i}| z) = \frac{P(z| x_{i})P(x_{i})}{P(z)} P(xi∣z)=P(z)P(z∣xi)P(xi)
这看起来有些难看,但实际上很简单。让我们找出右边每个词的意思:首先是 P ( z ∣ x i ) P(z| x_{i}) P(z∣xi),这是似然,也就是每个 x i x_{i} xi处观测值的准确性。 P ( x i ) P(x_{i}) P(xi)是先验——我们在包含观测值之前的概率。我们把它们相乘,这是update()函数中的非归一化乘法:
def update(likelihood, prior): posterior = prior * likelihood # p(z|x) * p(x) return normalize(posterior)
最后要考虑的是分母 P ( z ) P(z) P(z)。这是在不考虑位置的情况下获得观测值 z z z的概率。代码上,我们通过计算sum(belief)。这是我们计算归一化的方法!所以,update()函数只不过是在计算贝叶斯定理而已。
文献中经常以积分的形式给出这些方程。毕竟,积分只是连续函数的和。所以,你可能会看到贝叶斯定理被写成:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) ∫ P ( B ∣ A j ) P ( A j ) d A j P(A|B) = \frac{P(B|A)P(A)}{\int P(B|A_{j})P(A_{j})dA_{j} } P(A∣B)=∫P(B∣Aj)P(Aj)dAjP(B∣A)P(A)
这个分母通常是不可能用解析法求解的,就算它能被求解,在数学计算上也会非常困难。采用贝叶斯方法的滤波教科书中充满了积分方程,而积分往往没有解析解。但不要被这些方程吓倒,因为我们可以通过归一化后验概率来处理这个积分。在实践中,它只是一个归一化术语。
很可能你还没有完全明白贝叶斯定理的优点。我们要计算 p ( x i ∣ Z ) p(x_{i}|Z) p(xi∣Z),也就是说,在第 i i i步,给定一个观测值,计算我们的可能状态是什么。这是一个非常困难的问题,但又是很常见的。比如,根据癌症体检的结果,计算患癌症的概率;根据各种传感器的读数,计算下雨的概率等。
但是贝叶斯定理允许我们使用 p ( Z ∣ x i ) p(Z|x_{i}) p(Z∣xi)来计算这个,而这通常是很容易计算的:
p ( x i ∣ Z ) ∝ p ( Z ∣ x i ) p ( x i ) p(x_{i}|Z) \propto p(Z|x_{i})p(x_{i}) p(xi∣Z)∝p(Z∣xi)p(xi)
也就是说,为了计算给定特定传感器读数的下雨可能性,我们只需要计算给定下雨天气的传感器读数的可能性!这是一个容易得多的问题!好吧,天气预报仍然是一个难题,但是贝叶斯使它变得容易处理。
全概率定理
我们现在知道update()函数背后的数学原理,那么predict()函数呢?
predict()实现了全概率定理。让我们回忆一下update()的做法:它根据所有可能的运动事件来计算在任何给定位置的概率。假设在时间 t t t处于位置 i i i的概率可以写成 P ( X i t ) P(X_{i}^{t}) P(Xit)。那么,计算方式为: t − 1 t−1 t−1时刻处于所有可能位置 j j j的先验值 p ( X t − 1 j ) p(X_{t−1}^{j}) p(Xt−1j),乘以从对应 x j x_{j} xj移动到 x i {x_{i}} xi的概率,最后求和。即:
P ( X i t ) = ∑ j P ( X j t − 1 ) P ( x i ∣ x j ) P(X_{i}^{t}) = \sum_{j}^{} P(X_{j}^{t-1})P(x_{i}|x_{j}) P(Xit)=j∑P(Xjt−1)P(xi∣xj)
这个方程运用的就是全概率定理。引用维基百科:它表达了一个结果的总概率,这个结果可以通过几个不同的事件来实现。下面是计算这个等式的代码:
for i in range(N): for k in range (kN): index = (i + (width-k) - offset) % N result[i] += prob_dist[index] * kernel[k]
scipy.stats计算概率
在本文中,我使用FilterPy的代码来计算和绘制高斯函数。我这样做是为了让你有机会看看代码,看看这些函数是如何实现的。然而,Python在FilterPy的代码中附带了大量scipy.stats模块里的统计函数。让我们来看看如何使用scipy.stats来进行计算。
这个scipy.stats模块包含许多对象,你可以使用这些对象来计算各种分布的属性。本模块的完整文档如下:http://docs.scipy.org/doc/scipy/reference/stats.html。我们将重点讨论正态分布的实现:我们可以使用scipy.stats.norm来计算高斯函数,并将其结果与FilterPy模块的Gaussian()函数的返回值进行比较。
from scipy.stats import norm import filterpy.stats print(norm(2, 3).pdf(1.5)) print(filterpy.stats.gaussian(x=1.5, mean=2, var=3*3))
0.13114657203397997 0.13114657203397995
调用normal(2, 3)会创建并返回一个均值为2、标准差为3的对象,然后可以多次使用此对象来获得各种值的概率密度,例如:
n23 = norm(2, 3) print('pdf of 1.5 is %.4f' % n23.pdf(1.5)) print('pdf of 2.5 is also %.4f' % n23.pdf(2.5)) print('pdf of 2 is %.4f' % n23.pdf(2))
pdf of 1.5 is 0.1311 pdf of 2.5 is also 0.1311 pdf of 2 is 0.1330
scipy.stats.norm的文档列出许多其他函数。例如,我们可以使用rvs()函数从指定分布中生成 n n n个样本。
np.set_printoptions(precision=3, linewidth=50) print(n23.rvs(size=15))
[ 5.218 3.3 1.618 6.272 -0.711 6.019 -0.191 -1.357 1.698 -3.283 5.745 0.691 0.15 0.506 3.696]
我们也可以得到累积分布函数(cdf),它表示的是从分布中随机抽取的值小于或等于 x x x的概率。
# probability that a random value is less than the mean 2 print(n23.cdf(2))
0.5
当然,我们也可以得到分布的各种性质:
print('variance is', n23.var()) print('standard deviation is', n23.std()) print('mean is', n23.mean())
variance is 9.0 standard deviation is 3.0 mean is 2.0
用高斯函数模拟世界的局限性
前面我提到了中心极限定理,它指出:在某些条件下,任何独立随机变量的算术和都服从正态分布的,而无论该随机变量本身是如何分布的。这对我们来说很重要,因为自然界充满了非正太分布,但是当我们在大的总体上应用中心极限定理时,我们就得到了正态分布。
然而,中心极限定理的一个关键部分是在某些条件下。而这些条件通常不适用于物质世界,例如:厨房磅秤的读数不能低于零,但如果我们将观测误差表示为高斯,则曲线的左侧会延伸到负无穷远。这意味着也会给出负读数,尽管可能性非常小。
这是一个宽泛的话题,我不会详尽地讨论。
让我们考虑一个小例子。假设考试成绩服从正态分布,均值是90,标准差是13。因此,正态分布假设有人得到90分的可能性很大,有人得到40分的可能性很小。然而,这也意味着一个人获得-10或150分的可能性很小,同时也赋予了获得 − 1 0 300 -10^{300} −10300或 1 0 32986 10^{32986} 1032986分的极小机会。高斯分布的尾部是无限长的。
但对于成绩的结果我们知道这不是真的。忽略额外的条件,一般情况下,分数不得少于0或超过100。让我们用正态分布来绘制这个值范围,看看它代表真实的考试分数分布:
xs = np.arange(10, 100, 0.05) ys = [gaussian(x, 90, 30) for x in xs] plt.plot(xs, ys, label='var=0.2') plt.xlim(0, 120) plt.ylim(-0.02, 0.09)

这导致曲线下的面积不等于1,所以它不是概率分布。
同样,传感器观测中的误差很少是真正的高斯误差。现在谈论这给卡尔曼滤波器设计者带来的困难还为时过早。但值得记住的是,卡尔曼滤波器的数学模型是基于一个理想化的世界模型。现在,我将介绍一些代码,可能在后面的章节中会使用这些代码来形成分布,以模拟各种传感器。这种分布称为t分布。
假设我想模拟一个输出中有白噪声的传感器。为简单起见,假设信号为常数10,噪声的标准差为2。我们可以使用这个函数numpy.random.randn()得到一个均值为0,标准差为1的随机数。我可以用以下方法来模拟:
from numpy.random import randn def sense(): return 10 + randn()*2
让我们画出这个信号,看看它是什么样子。
zs = [sense() for i in range(5000)] plt.plot(zs, lw=1)

这看起来像是我所期望的。信号集中在10左右,标准差为2意味着 68 % 68\% 68%的观测值将在10的 ± 2 \pm 2 ±2范围内, 99 % 99\% 99%的观测值将在10的 ± 6 \pm 6 ±6范围内,这和图像中的样子很类似。
现在让我们看一下用t分布。我将不介绍数学知识,只给你源代码,然后用它绘制一个分布。
import random import math def rand_student_t(df, mu=0, std=1): """return random number distributed by Student's t distribution with `df` degrees of freedom with the specified mean and standard deviation. """ x = random.gauss(0, std) y = 2.0*random.gammavariate(0.5*df, 2.0) return x / (math.sqrt(y / df)) + mu
def sense_t(): return 10 + rand_student_t(7)*2 zs = [sense_t() for i in range(5000)] plt.plot(zs, lw=1)
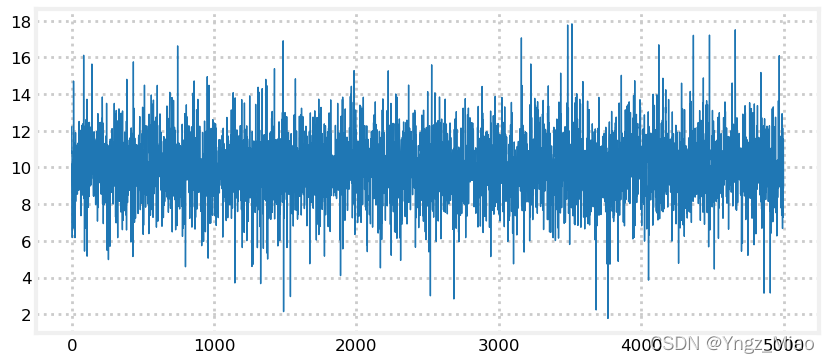
我们可以从图中看到,虽然输出类似于正态分布,但也有离群值远远超过均值的 3 σ 3\sigma 3σ(7到13)。
t分布也不太可能是传感器性能的精确模型,然而它确实能产生更合理的数据来测试滤波器在实际噪声中的性能。
这不是无谓的担忧。卡尔曼滤波方程假设噪声是正态分布的,如果不是这样,则执行效果就不怎么好了。一些关键任务上的滤波器(如航天器上的滤波器)的设计者需要掌握大量有关航天器上传感器性能的理论和经验知识。例如,我在美国宇航局的一次任务中看到的一个演示表明,虽然理论上他们应该使用3个标准差来区分噪声和实际观测值,但他们实际上使用的是5到6个标准差。这是他们通过实验确定的。
rand_student_t的代码包含在filterpy.stats文件中,你可以使用:
from filterpy.stats import rand_student_t
高斯积(可选)
这里我导出了两个高斯函数乘积的方程。
你可以通过将两个高斯方程相乘,再合并项找到这个结果,但是这样做的计算过程会变得很混乱。我将用贝叶斯定理导出它。我们可以把这个问题简化成:让先验概率服从 N ( μ ˉ , σ ˉ 2 ) N(\bar{\mu} , \bar{\sigma }^{2} ) N(μˉ,σˉ2),观测值 z ∝ N ( z , σ z 2 ) z \propto N(z, \sigma _{z}^{2} ) z∝N(z,σz2)。最终需要计算给定观测值 z z z后的后验概率是多少?
将后验概率写为 p ( x ∣ z ) p(x|z) p(x∣z)。现在我们可以用贝叶斯定理来说明:
p ( x ∣ z ) = p ( z ∣ x ) p ( x ) P ( z ) p(x|z) = \frac{p(z|x)p(x)}{P(z)} p(x∣z)=P(z)p(z∣x)p(x)
p ( z ) p(z) p(z)是归一化常数,所以我们可以简化为:
p ( x ∣ z ) ∝ p ( z ∣ x ) p ( x ) p(x|z) \propto p(z|x)p(x) p(x∣z)∝p(z∣x)p(x)
现在我们代入高斯方程:
p ( z ∣ x ) = 1 2 π σ z 2 e x p [ − ( z − x ) 2 2 σ z 2 ] p(z|x) = \frac{1}{\sqrt[]{2\pi \sigma _{z}^{2}} }exp[-\frac{(z-x)^{2}}{2\sigma _{z}^{2}} ] p(z∣x)=2πσz21exp[−2σz2(z−x)2]
p ( x ) = 1 2 π σ ˉ 2 e x p [ − ( x − μ ˉ ) 2 2 σ ˉ 2 ] p(x) = \frac{1}{\sqrt[]{2\pi \bar{\sigma }^{2}} }exp[-\frac{(x-\bar{ \mu} )^{2}}{2\bar{\sigma }^{2}} ] p(x)=2πσˉ21exp[−2σˉ2(x−μˉ)2]
我们可以去掉前导项,因为它们是常量:
p ( x ∣ z ) ∝ e x p [ − ( z − x ) 2 2 σ z 2 ] e x p [ − ( x − μ ˉ ) 2 2 σ ˉ 2 ] p(x|z) \propto exp[-\frac{(z-x)^{2}}{2\sigma _{z}^{2}} ]exp[-\frac{(x-\bar{ \mu} )^{2}}{2\bar{\sigma }^{2}} ] p(x∣z)∝exp[−2σz2(z−x)2]exp[−2σˉ2(x−μˉ)2]
∝ e x p [ − ( z − x ) 2 2 σ z 2 − ( x − μ ˉ ) 2 2 σ ˉ 2 ] \propto exp[-\frac{(z-x)^{2}}{2\sigma _{z}^{2}} -\frac{(x-\bar{ \mu} )^{2}}{2\bar{\sigma }^{2}}] ∝exp[−2σz2(z−x)2−2σˉ2(x−μˉ)2]
∝ e x p [ − 1 2 σ z 2 σ ˉ 2 [ σ ˉ 2 ( z − x ) 2 + σ z 2 ( x − μ ˉ ) 2 ] ] \propto exp[-\frac{1}{2\sigma _{z}^{2}\bar{ \sigma }^{2}} [\bar{ \sigma }^{2}(z-x)^{2} + \sigma _{z}^{2}(x - \bar{\mu } )^{2}]] ∝exp[−2σz2σˉ21[σˉ2(z−x)2+σz2(x−μˉ)2]]
现在我们乘出平方项,然后根据后验 x x x进行分组。
p ( x ∣ z ) ∝ e x p [ − 1 2 σ z 2 σ ˉ 2 [ σ ˉ 2 ( z 2 − 2 x z + x 2 ) + σ z 2 ( x 2 − 2 x μ ˉ + μ ˉ 2 ) ] ] p(x|z) \propto exp[-\frac{1}{2\sigma _{z}^{2}\bar{ \sigma }^{2}} [\bar{ \sigma }^{2}(z^{2} - 2xz + x^{2}) + \sigma _{z}^{2}(x^{2} - 2x\bar{\mu } +\bar{\mu }^{2} )]] p(x∣z)∝exp[−2σz2σˉ21[σˉ2(z2−2xz+x2)+σz2(x2−2xμˉ+μˉ2)]]
∝ e x p [ − 1 2 σ z 2 σ ˉ 2 [ x 2 ( σ ˉ 2 + σ z 2 ) − 2 x ( σ z 2 μ ˉ + σ ˉ 2 z ) + ( σ ˉ 2 z 2 + σ z 2 μ ˉ 2 ) ] ] \propto exp[-\frac{1}{2\sigma _{z}^{2}\bar{ \sigma }^{2}} [x^{2}(\bar{\sigma }^{2} + \sigma _{z}^{2} ) - 2x(\sigma _{z}^{2}\bar{\mu } + \bar{\sigma }^{2}z) + (\bar {\sigma } ^{2}z^{2} + \sigma _{z}^{2}\bar{\mu }^{2} )]] ∝exp[−2σz2σˉ21[x2(σˉ2+σz2)−2x(σz2μˉ+σˉ2z)+(σˉ2z2+σz2μˉ2)]]
最后一个括号不包含后面的 x x x,因此可以将其视为常量并丢弃。
p ( x ∣ z ) ∝ e x p [ − 1 2 σ z 2 σ ˉ 2 [ x 2 ( σ ˉ 2 + σ z 2 ) − 2 x ( σ z 2 μ ˉ + σ ˉ 2 z ) ] ] p(x|z) \propto exp[-\frac{1}{2\sigma _{z}^{2}\bar{ \sigma }^{2}} [x^{2}(\bar{\sigma }^{2} + \sigma _{z}^{2} ) - 2x(\sigma _{z}^{2}\bar{\mu } + \bar{\sigma }^{2}z) ]] p(x∣z)∝exp[−2σz2σˉ21[x2(σˉ2+σz2)−2x(σz2μˉ+σˉ2z)]]
将分子和分母除以 σ ˉ 2 + σ z 2 \bar {\sigma}^{2} + \sigma _{z}^{2} σˉ2+σz2得到:
p ( x ∣ z ) ∝ e x p [ − 1 2 x 2 − 2 x ( σ z 2 μ ˉ + σ ˉ 2 z ) σ ˉ 2 + σ z 2 σ z 2 σ ˉ 2 σ ˉ 2 + σ z 2 ] p(x|z) \propto exp[-\frac{1}{2} \frac{x^{2} - 2x(\frac{\sigma _{z}^{2}\bar{\mu } + \bar{\sigma }^{2}z) }{\bar {\sigma}^{2} + \sigma _{z}^{2}} }{\frac{\sigma _{z}^{2}\bar{ \sigma }^{2}}{\bar {\sigma}^{2} + \sigma _{z}^{2}} }] p(x∣z)∝exp[−21σˉ2+σz2σz2σˉ2x2−2x(σˉ2+σz2σz2μˉ+σˉ2z)]
比例性允许我们随意创建或删除常量,因此我们可以将其考虑到:
p ( x ∣ z ) ∝ e x p [ − 1 2 ( x − σ z 2 μ ˉ + σ ˉ 2 z σ ˉ 2 + σ z 2 ) 2 σ z 2 σ ˉ 2 σ ˉ 2 + σ z 2 ] p(x|z) \propto exp[-\frac{1}{2} \frac{(x-\frac{\sigma _{z}^{2}\bar{\mu } + \bar{\sigma }^{2}z }{\bar {\sigma}^{2} + \sigma _{z}^{2}} )^{2}}{\frac{\sigma _{z}^{2}\bar{ \sigma }^{2}}{\bar {\sigma}^{2} + \sigma _{z}^{2}} }] p(x∣z)∝exp[−21σˉ2+σz2σz2σˉ2(x−σˉ2+σz2σz2μˉ+σˉ2z)2]
一个高斯函数类似于:
N ( μ , σ 2 ) ∝ e x p [ − 1 2 ( x − μ ) 2 σ 2 ] N(\mu , \sigma ^{2}) \propto exp[-\frac{1}{2}\frac{(x-\mu )^{2}}{\sigma ^{2}} ] N(μ,σ2)∝exp[−21σ2(x−μ)2]
所以我们可以看到 p ( x ∣ z ) p(x|z) p(x∣z)的均值为:
μ p o s t e r i o r = σ z 2 μ ˉ + μ ˉ 2 z σ ˉ 2 + σ z 2 \mu _{posterior} = \frac{\sigma _{z}^{2}\bar{\mu }+\bar{\mu }^{2}z }{\bar{\sigma }^{2} + \sigma _{z}^{2} } μposterior=σˉ2+σz2σz2μˉ+μˉ2z
方差为:
σ p o s t e r i o r 2 = σ z 2 σ ˉ 2 σ ˉ 2 + σ z 2 \sigma _{posterior}^{2} = \frac{\sigma _{z}^{2}\bar{\sigma }^{2} }{\bar{\sigma }^{2}+\sigma _{z}^{2} } σposterior2=σˉ2+σz2σz2σˉ2
我去掉了常数,所以结果不是正常的,而是成比例的。贝叶斯定理用 p ( z ) p(z) p(z)因子归一化,确保结果是归一化的。我们在滤波器的更新步骤中进行归一化,确保滤波器的估计是高斯的。
N 1 = ∣ N 2 ⋅ N 3 ∣ N_{1} = |N_{2}\cdot N_{3}| N1=∣N2⋅N3∣
高斯和(可选)
这里我导出了两个高斯函数和的方程。
两个高斯的和由下式给出:
μ = μ 1 + μ 2 \mu = \mu_{1} + \mu_{2} μ=μ1+μ2
σ 2 = σ 1 2 + σ 2 2 \sigma ^{2} = \sigma_{1}^{2} + \sigma_{2}^{2} σ2=σ12+σ22
这有几个证据。我将使用卷积,因为我们在上一篇文章中使用卷积来表示概率的直方图。
为了求两个高斯随机变量之和的密度函数,我们先对每个变量的密度函数求和。它们是非线性的连续函数,所以我们需要用积分来计算和。如果随机变量 p p p和 z z z(如先验和观测)是独立的,我们可以用:
p ( x ) = ∫ − ∞ ∞ f p ( x − z ) f z ( z ) d x p(x) = \int_{-\infty }^{\infty } f_{p}(x-z)f_{z}(z)dx p(x)=∫−∞∞fp(x−z)fz(z)dx
这是一个卷积方程。现在我们来算一下:
p ( x ) = ∫ − ∞ + ∞ f 2 ( x − x 1 ) f 1 ( x 1 ) d x p(x) = \int _{-\infty}^{+\infty} f_2(x-x_1)f_1(x_1)dx p(x)=∫−∞+∞f2(x−x1)f1(x1)dx
= ∫ − ∞ + ∞ 1 2 π σ z exp [ − ( x − z − μ z ) 2 2 σ z 2 ] 1 2 π σ p exp [ − ( x − μ p ) 2 2 σ p 2 ] d x = \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}\sigma_{z}}\exp\left[-\frac{(x - z - \mu_{z})^{2}}{2\sigma^{2}_{z}}\right] \frac{1}{\sqrt{2\pi}\sigma_{p}}\exp\left[-\frac{(x - \mu_{p})^{2}}{2\sigma^{2}_{p}}\right] dx =∫−∞+∞2πσz1exp[−2σz2(x−z−μz)2]2πσp1exp[−2σp2(x−μp)2]dx
= ∫ − ∞ + ∞ 1 2 π σ p 2 + σ z 2 exp [ − ( x − ( μ p + μ z ) ) ) 2 2 ( σ z 2 + σ p 2 ) ] 1 2 π σ p σ z σ p 2 + σ z 2 exp [ − ( x − σ p 2 ( x − μ z ) + σ z 2 μ p ) ) 2 2 ( σ p σ x σ z 2 + σ p 2 ) 2 ] d x = \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}\sqrt{\sigma_{p}^{2} + \sigma_{z}^{2}}} \exp\left[ -\frac{(x - (\mu_{p} + \mu_{z})))^{2}}{2(\sigma_{z}^{2}+\sigma_{p}^{2})}\right] \frac{1}{\sqrt{2\pi}\frac{\sigma_{p}\sigma_{z}}{\sqrt{\sigma_{p}^{2} + \sigma_{z}^{2}}}} \exp\left[ -\frac{(x - \frac{\sigma_{p}^{2}(x-\mu_{z}) + \sigma_{z}^{2}\mu_{p}}{}))^{2}}{2\left(\frac{\sigma_{p}\sigma_{x}}{\sqrt{\sigma_{z}^{2}+\sigma_{p}^{2}}}\right)^{2}}\right]dx =∫−∞+∞2πσp2+σz21exp[−2(σz2+σp2)(x−(μp+μz)))2]2πσp2+σz2σpσz1exp −2(σz2+σp2σpσx)2(x−σp2(x−μz)+σz2μp))2 dx
= 1 2 π σ p 2 + σ z 2 exp [ − ( x − ( μ p + μ z ) ) ) 2 2 ( σ z 2 + σ p 2 ) ] ∫ − ∞ + ∞ 1 2 π σ p σ z σ p 2 + σ z 2 exp [ − ( x − σ p 2 ( x − μ z ) + σ z 2 μ p ) ) 2 2 ( σ p σ x σ z 2 + σ p 2 ) 2 ] d x = \frac{1}{\sqrt{2\pi}\sqrt{\sigma_{p}^{2} + \sigma_{z}^{2}}} \exp\left[ -\frac{(x - (\mu_{p} + \mu_{z})))^{2}}{2(\sigma_{z}^{2}+\sigma_{p}^{2})}\right] \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}\frac{\sigma_{p}\sigma_{z}}{\sqrt{\sigma_{p}^{2} + \sigma_{z}^{2}}}} \exp\left[ -\frac{(x - \frac{\sigma_{p}^{2}(x-\mu_{z}) + \sigma_{z}^{2}\mu_{p}}{}))^{2}}{2\left(\frac{\sigma_{p}\sigma_{x}}{\sqrt{\sigma_{z}^{2}+\sigma_{p}^{2}}}\right)^{2}}\right]dx =2πσp2+σz21exp[−2(σz2+σp2)(x−(μp+μz)))2]∫−∞+∞2πσp2+σz2σpσz1exp −2(σz2+σp2σpσx)2(x−σp2(x−μz)+σz2μp))2 dx
积分中的表达式是正态分布。正态分布的和是1,因此积分是1。这给了我们:
p ( x ) = 1 2 π σ p 2 + σ z 2 exp [ − ( x − ( μ p + μ z ) ) ) 2 2 ( σ z 2 + σ p 2 ) ] p(x) = \frac{1}{\sqrt{2\pi}\sqrt{\sigma_{p}^{2} + \sigma_{z}^{2}}} \exp\left[ -\frac{(x - (\mu_{p} + \mu_{z})))^{2}}{2(\sigma_{z}^{2}+\sigma_{p}^{2})}\right] p(x)=2πσp2+σz21exp[−2(σz2+σp2)(x−(μp+μz)))2]
这是一个高斯分布的正常形式,其中:
μ x = μ p + μ z \mu_{x} = \mu_{p} + \mu_{z} μx=μp+μz
σ x 2 = σ p 2 + σ z 2 \sigma_{x}^{2} = \sigma_{p}^{2} + \sigma_{z}^{2} σx2=σp2+σz2
总结和要点
本文对统计学的总体介绍很少,我只讨论了需要使用的高斯函数的概念,其他很少赘述。在我们继续之前,你必须了解以下几点:
- 高斯分布表示一个连续的概率分布;
- 它们完全由两个参数来描述:均值( μ \mu μ)和方差( σ 2 \sigma^{2} σ2);
- μ \mu μ是所有可能值的均值;
- 方差 σ 2 \sigma^{2} σ2表示我们的观测值与均值的差异;
- 标准差( σ \sigma σ)是方差( σ 2 \sigma^{2} σ2)的平方根;
- 自然界中许多事物近似于正态分布,但并不完美;
- 在滤波问题中,计算 p ( x ∣ z ) p(x|z) p(x∣z)几乎是不可能的,但是计算 p ( z ∣ x ) p(z|x) p(z∣x)是简单的。贝叶斯定理让我们从后者计算前者。


 0
0









