,本文就讲一下用verilog实现cordic算法的NCO代码。
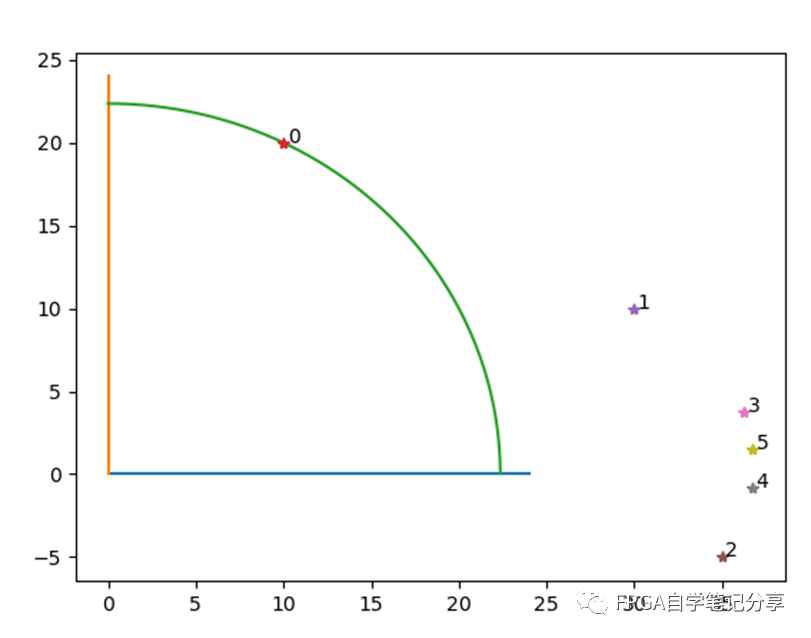
上文讲到cordic的计算公式为:
X1=cos(θ)(X0-Y0*tan(θ))Y1=cos(θ)(Y0+X0*tan(θ))其中cos(θ)可以根据最终的迭代次数直接得到,但是上式中还有一个tan(θ)的乘法操作,FPGA在实现cordic算法时会对其进行进一步优化,将tan(θ)的取值设置为1,0.5,0.25.... (这些值在verilog数字硬件中就对应为1/2^0,1/2^1,1/2^2 ...)cordic的旋转角度为对应的角度值,这样在verilog中tan(θ)的乘法操作可以使用移位直接实现,cordic中就没有乘法操作了。最终可以得到下表:|
序号 |
正切值 |
弧度值 |
角度值 |
正弦值 |
gain |
|
0 |
1 |
0.785398 |
45 |
0.707107 |
0.707107 |
|
1 |
0.5 |
0.463648 |
26.56505 |
0.894427 |
0.632456 |
|
2 |
0.25 |
0.244979 |
14.03624 |
0.970143 |
0.613572 |
|
3 |
0.125 |
0.124355 |
7.125016 |
0.992278 |
0.608834 |
|
4 |
0.0625 |
0.062419 |
3.576334 |
0.998053 |
0.607648 |
|
5 |
0.03125 |
0.03124 |
1.789911 |
0.999512 |
0.607352 |
|
6 |
0.015625 |
0.015624 |
0.895174 |
0.999878 |
0.607278 |
|
7 |
0.007813 |
0.007812 |
0.447614 |
0.999969 |
0.607259 |
|
8 |
0.003906 |
0.003906 |
0.223811 |
0.999992 |
0.607254 |
表中第一列为序号,表征cordic的迭代次数,第二类为tan(θ)的值,第三列第四列是正切值求得的弧度值和角度值,第五列是角度对应的正弦值,最后一列是增益,就是cos(θ)的乘积。
Verilog代码实现NCO的方法:1、对角度值选取合适的量化位宽;2、输出量化位宽选择;3、根据精度选取迭代次数;4、确定增益及增益量化位宽;*最大误差就是最终的正切角度。*注意角度溢出的处理。代码如下:端口:
// ============================================================// File Name: cm_nco_cordic// VERSION : V1.0// DATA : 2022/11/20// Author : FPGA干货分享// ============================================================// 功能:NCO生成代码 cordic// delay : // ============================================================ `timescale 1ns/100psmodule cm_nco_cordic parameter C_DATA_WITH = 11 )( input wire I_sys_clk , /// 工作时钟 100M input wire [14:0] I_angle , /// 角度值,2*13 = π/4 output reg [C_DATA_WITH-1:0] O_sin_out , /// 输出正弦值 output reg [C_DATA_WITH-1:0] O_cos_out /// 输出余弦值);
参数化增益,这里使用4096对应45度:
// ============================================================// parameter// ============================================================localparam C_ATAN0 = 13'd4096 ; ///弧度量化 localparam C_ATAN1 = 13'd2418 ; ///弧度量化 localparam C_ATAN2 = 13'd1278 ; ///弧度量化 localparam C_ATAN3 = 13'd649 ; ///弧度量化 localparam C_ATAN4 = 13'd326 ; ///弧度量化 localparam C_ATAN5 = 13'd163 ; ///弧度量化 localparam C_ATAN6 = 13'd81 ; ///弧度量化 localparam C_ATAN7 = 13'd41 ; ///弧度量化 localparam C_ATAN8 = 13'd20 ; ///弧度量化 localparam C_GAIN = 2**(C_DATA_WITH-1) -1;
代码首先对象限信息进行打拍,方便cos,sin值得输出:
always @(posedge I_sys_clk) begin S_ang_d1 <= I_angle[14:13]; S_ang_d2 <= S_ang_d1; S_ang_d3 <= S_ang_d2; S_ang_d4 <= S_ang_d3; S_ang_d5 <= S_ang_d4; S_ang_d6 <= S_ang_d5; S_ang_d7 <= S_ang_d6; S_ang_d8 <= S_ang_d7; S_ang_d9 <= S_ang_d8; S_ang_d10 <= S_ang_d9; end
cordic迭代:
/// 第一次循环 x0=C_GAIN y0=0/// x_n = x - y/(2**n)/// y_n = y + x/(2**n)/// ang = ang - angele[i]always @(posedge I_sys_clk) begin S_x_1 <= C_GAIN ; S_y_1 <= C_GAIN ; S_a_1 <= {1'b0,I_angle[12:0]}-C_ATAN0; end /// 第二次循环/// if(S_a_1<0):/// x_n = x + y/(2**1)/// y_n = y - x/(2**1)/// ang = ang + angele[i]/// else:/// x_n = x - y/(2**1)/// y_n = y + x/(2**1)/// ang = ang - angele[i] always @(posedge I_sys_clk) if(S_a_1[13]) begin S_x_2 <= S_x_1 + {S_y_1[C_DATA_WITH],S_y_1[C_DATA_WITH:1]} ; S_y_2 <= S_y_1 - {S_x_1[C_DATA_WITH],S_x_1[C_DATA_WITH:1]} ; S_a_2 <= S_a_1 + C_ATAN1 ; end else begin S_x_2 <= S_x_1 - {S_y_1[C_DATA_WITH],S_y_1[C_DATA_WITH:1]} ; S_y_2 <= S_y_1 + {S_x_1[C_DATA_WITH],S_x_1[C_DATA_WITH:1]} ; S_a_2 <= S_a_1 - C_ATAN1 ; end /// 第三次循环/// if(S_a_2<0):/// x_n = x + y/(2**2)/// y_n = y - x/(2**2)/// ang = ang + angele[i]/// else:/// x_n = x - y/(2**2)/// y_n = y + x/(2**2)/// ang = ang - angele[i] always @(posedge I_sys_clk) if(S_a_2[13]) begin S_x_3 <= S_x_2 + {{2{S_y_2[C_DATA_WITH]}},S_y_2[C_DATA_WITH:2]} ; S_y_3 <= S_y_2 - {{2{S_x_2[C_DATA_WITH]}},S_x_2[C_DATA_WITH:2]} ; S_a_3 <= S_a_2 + C_ATAN2 ; end else begin S_x_3 <= S_x_2 - {{2{S_y_2[C_DATA_WITH]}},S_y_2[C_DATA_WITH:2]} ; S_y_3 <= S_y_2 + {{2{S_x_2[C_DATA_WITH]}},S_x_2[C_DATA_WITH:2]} ; S_a_3 <= S_a_2 - C_ATAN2 ; end /// 第四次循环/// if(S_a_3<0):/// x_n = x + y/(2**3)/// y_n = y - x/(2**3)/// ang = ang + angele[i]/// else:/// x_n = x - y/(2**3)/// y_n = y + x/(2**3)/// ang = ang - angele[i] always @(posedge I_sys_clk) if(S_a_3[13]) begin S_x_4 <= S_x_3 + {{3{S_y_3[C_DATA_WITH]}},S_y_3[C_DATA_WITH:3]} ; S_y_4 <= S_y_3 - {{3{S_x_3[C_DATA_WITH]}},S_x_3[C_DATA_WITH:3]} ; S_a_4 <= S_a_3 + C_ATAN3 ; end else begin S_x_4 <= S_x_3 - {{3{S_y_3[C_DATA_WITH]}},S_y_3[C_DATA_WITH:3]} ; S_y_4 <= S_y_3 + {{3{S_x_3[C_DATA_WITH]}},S_x_3[C_DATA_WITH:3]} ; S_a_4 <= S_a_3 - C_ATAN3 ; end always @(posedge I_sys_clk) if(S_a_4[13]) begin S_x_5 <= S_x_4 + {{4{S_y_4[C_DATA_WITH]}},S_y_4[C_DATA_WITH:4]} ; S_y_5 <= S_y_4 - {{4{S_x_4[C_DATA_WITH]}},S_x_4[C_DATA_WITH:4]} ; S_a_5 <= S_a_4 + C_ATAN4 ; end else begin S_x_5 <= S_x_4 - {{4{S_y_4[C_DATA_WITH]}},S_y_4[C_DATA_WITH:4]} ; S_y_5 <= S_y_4 + {{4{S_x_4[C_DATA_WITH]}},S_x_4[C_DATA_WITH:4]} ; S_a_5 <= S_a_4 - C_ATAN4 ; end always @(posedge I_sys_clk) if(S_a_5[13]) begin S_x_6 <= S_x_5 + {{5{S_y_5[C_DATA_WITH]}},S_y_5[C_DATA_WITH:5]} ; S_y_6 <= S_y_5 - {{5{S_x_5[C_DATA_WITH]}},S_x_5[C_DATA_WITH:5]} ; S_a_6 <= S_a_5 + C_ATAN5 ; end else begin S_x_6 <= S_x_5 - {{5{S_y_5[C_DATA_WITH]}},S_y_5[C_DATA_WITH:5]} ; S_y_6 <= S_y_5 + {{5{S_x_5[C_DATA_WITH]}},S_x_5[C_DATA_WITH:5]} ; S_a_6 <= S_a_5 - C_ATAN5 ; end ///数据溢出特殊处理assign S_x_6_abs = S_x_6[C_DATA_WITH] ? (~S_x_6 + 1) : S_x_6 ;assign S_y_6_abs = S_y_6[C_DATA_WITH] ? (~S_y_6 + 1) : S_y_6 ;
迭代结果要与增益相乘,x*0.6 = x*622/1024,这里我们是基于xilinx的dsp48写的乘法器,大家可以根据需要替换这个乘法器即可:
/// x*0.6 = x*622/1024cm_dsp48e1 #( .C_DATA_WITH_A (C_DATA_WITH+1 ), .C_DATA_WITH_B (12 ), .C_DATA_WITH_C (12 ), .C_DATA_WITH_D (25 ))U0_cm_dsp48e1( .I_CLK (I_sys_clk ) , // clk .I_RST ('d0 ) , // RST .I_A (S_x_6_abs ) , // [29:0] .I_B (12'd622 ) , // [17:0] .I_C (12'd512 ) , // [47:0] .I_D (25'd0 ) , // [24:0] .I_PCIN (48'd0 ) , // [47:0] 只能直连PCOUT .I_ALUMODE (4'd0 ) , // [3:0] .I_INMODE (5'b00101 ) , // [4:0] d+a1 .I_OPMODE (7'b0110101 ) , // [6:0] .O_P (S_x_dsp ) , // [47:0] .O_PCOUT ( ) // [47:0] 只能直连PCIN ); cm_dsp48e1 #( .C_DATA_WITH_A (C_DATA_WITH+1 ), .C_DATA_WITH_B (12 ), .C_DATA_WITH_C (12 ), .C_DATA_WITH_D (25 ))U1_cm_dsp48e1( .I_CLK (I_sys_clk ) , // clk .I_RST ('d0 ) , // RST .I_A (S_y_6_abs ) , // [29:0] .I_B (12'd622 ) , // [17:0] .I_C (12'd512 ) , // [47:0] .I_D (25'd0 ) , // [24:0] .I_PCIN (48'd0 ) , // [47:0] 只能直连PCOUT .I_ALUMODE (4'd0 ) , // [3:0] .I_INMODE (5'b00101 ) , // [4:0] d+a1 .I_OPMODE (7'b0110101 ) , // [6:0] .O_P (S_y_dsp ) , // [47:0] .O_PCOUT ( ) // [47:0] 只能直连PCIN );
最后根据输入的象限得到最终输出:
always @(posedge I_sys_clk) == 2'd0) begin O_cos_out <= S_x_dsp[C_DATA_WITH+:10]; O_sin_out <= S_y_dsp[C_DATA_WITH+:10]; end else if(S_ang_d10 == 2'd1) begin O_cos_out <= -(S_y_dsp[C_DATA_WITH+:10]); O_sin_out <= S_x_dsp[C_DATA_WITH+:10]; end else if(S_ang_d10 == 2'd2) begin O_cos_out <= -(S_x_dsp[C_DATA_WITH+:10]); O_sin_out <= -(S_y_dsp[C_DATA_WITH+:10]); end else begin O_cos_out <= (S_y_dsp[C_DATA_WITH+:10]); O_sin_out <= -(S_x_dsp[C_DATA_WITH+:10]); end
上边的象限判断,我们在FPGA数字信号处理之verilog实现NCO(代码及仿真)里边已经详细说过,这里就放一张图如下,不理解的可以看之前的文章。

最后对其仿真:
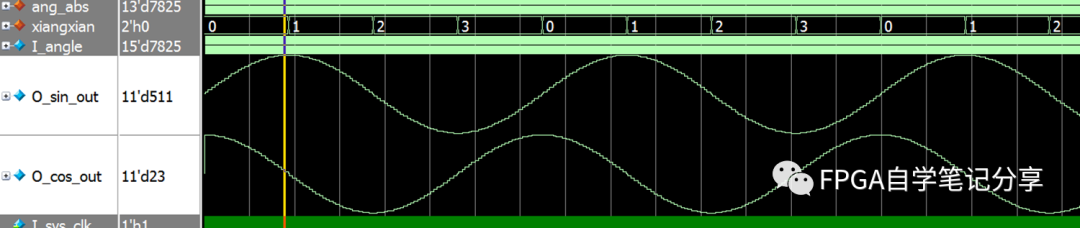


 0
0









