一、二进制数与数制

1、 进位计数制 十进制数是人们习惯使用的进制。计算机只能“识别”二进制数。为了书写和识读方便，计算机程序需要用十六进制数表示。十进制数、二进制数、十六进制数之间的关系、相互转换和运算方法，是学习计算机必备的基础知识。 二进制数是计算机工作的基础，在计算机中只能使用二进制数。 所有指令、数据、字符和地址的表示，以及它们的存储、处理和传送都是以二进制形式进行的，因此计算机的电路逻辑和处理方法也都是按二进制的原则实现的。没有二进制就没有电子计算机。 进位数制具有如下特点：

•  每一种进位数制的数字符号的个数等于计数制的基数；
•  逢基数进一；
•  数字的权与其位置有关，且为基数的幂的形式

2、 二进制数及在计算机中的应用 （1）二进制数（Binary） 特点：基数是2。 只有两个数码：0 和1； 进位规则是“逢二进一”； 每左移一位,数值增大一倍；右移一位,数值减小一半； 二进制数用尾缀B作为标识符。

（2）位（bit）  指二进制数的位。位是数的最小单位，中文称作“比特”。 （3）字节（Byte） 8位二进制数成为一个字节，常用大写字母B表示。字节是最基本的数据单位，计算机的数据、代码、指令、地址多以字节为单位。 （4）字（Word） 字是一台计算机上所能并行处理的二进制数，字的位数（或长度）称之为字长。字长必须是字节的整数倍。 如MCS-51单片机字长为8位，MCS-96单片机字长为16位，在微机中还有32位、64位的计算机。

3.  二进制数运算

算数运算：

逻辑运算：

4、十进制数（decimal）
主要特点： ① 基数是10。有10个数码（数符）构成： 0、1、2、3、4、5、6、7、8、9。 ② 进位规则是“逢十进一”。

5、十六进制数（Hexadecimal）

主要特点：

① 基数是16。共有16个数符构成：

0、1、…、9、A、B、C、D、E、F。其中，

A、B、C、D、E、F 代表的数值分别为

10、11、12、13、14、15。

② 进位规则是“逢十六进一”。

十六进制数用尾缀H表示。

十六进制数、二进制数和十进制数对应关系表

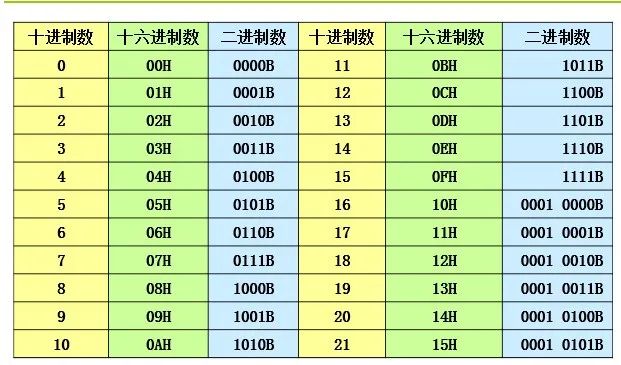
二、 计算机中数据的表示方法

1 、原码、反码和补码

原码、反码和补码对应关系表

2. 常用编码 （1）8421 BCD码 称为二-十进制数或简称BCD码 (BinaryCoded Decimal Code)，用标识符[……]BCD表示。 ① 编码方法
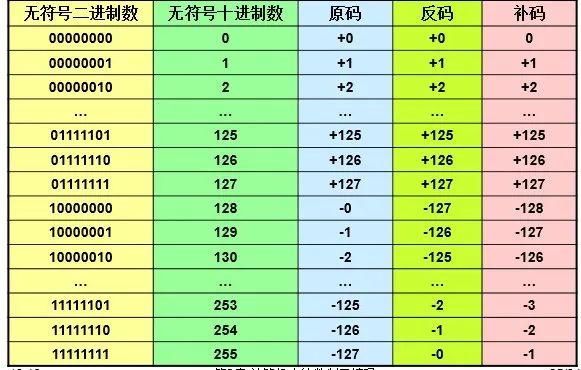
 二-十进制数是十进制数，逢十进一，只是数符0～9用4位二进制码 0000 ～ 1001 表示而已；
  每4位以内按二进制进位；
 4位与4位之间按十进制进位。
② 转换关系
  （a）BCD码与十进制数相互转换关系
  （b）BCD码与二进制数相互转换关系     BCD码与二进制数之间不能直接相互转换，通常要先转换成十进制数。

BCD码运算

BCD码用4位二进制数表示，但4位二进制数最多可表示16种状态，余下6种状态，1010～1111在BCD编码中称为非法码或冗余码。在BCD码的运算中将会出现冗余码，需要作某些修正，才能得到正确的结果。 修正方法：

       若相加后的低4位（或高4位）二进制数大于9，或大于15（即低4位或高4位的最高位有进位），则应对低4位（或高4位）加6修正。

（2）ASCII码 作用：用二进制编码表示各种字母和符号ASCII码（AmericanStanded Code for Information Interchange，美国信息交换标准代码）。

ASCII编码表

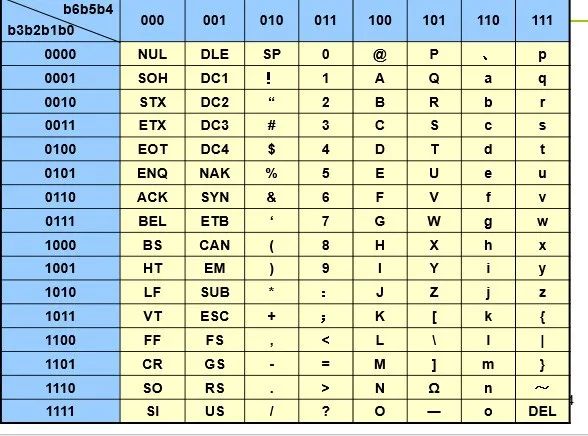早期的ASCII码采用7位二进制代码对字符进行编码。 它包括32个通用控制字符，10个阿拉伯数字，52个英文大，小字母，34个专用符号共128个。 7位ASCII代码在最高位添加一个“0”组成8位代码，正好占一个字节，在存储和传输信息中，最高位常作为奇偶校验位使用。扩展ASCII码，即第八位不再视为校验位而是当作编码位使用。扩展 ASCII码有256个。 温馨提示：几个常用数值 1K=1024=210 1M=1024K=220 1G=1024M=230 1T=1024G=240 216=26×210=64K=65536 4K=22×210，相应的数值变化范围是12个0到12个1，即000H~FFFH