Smith 圆图是射频电路设计中最常用的工具之一,Smith圆图是大神Philip Hagar Smith在贝尔实验室工作时开发的,我们在前面的文章中多次重点介绍过。
今天,我们通过几个例子来看一下,在射频设计中,如何使用Smith圆图进行阻抗匹配。例子来自于《微波工程》,今天搬出来,再学习一遍。
问题:
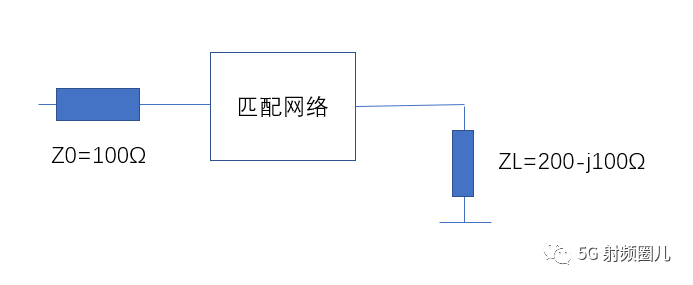
设计一个L型匹配网络,使其在频率500MHz处,完成负载到传输线的匹配。负载阻抗为ZL=200-j100Ω,传输线阻抗为Z0=100Ω。 这个问题的示意图如下:
 常见的L型匹配电路有两种,左L和右L,具体选择哪种,可根据源阻抗与负载阻抗的大小关系来定S( 不得不掌握的几种常见的集总参数阻抗匹配电路 )。
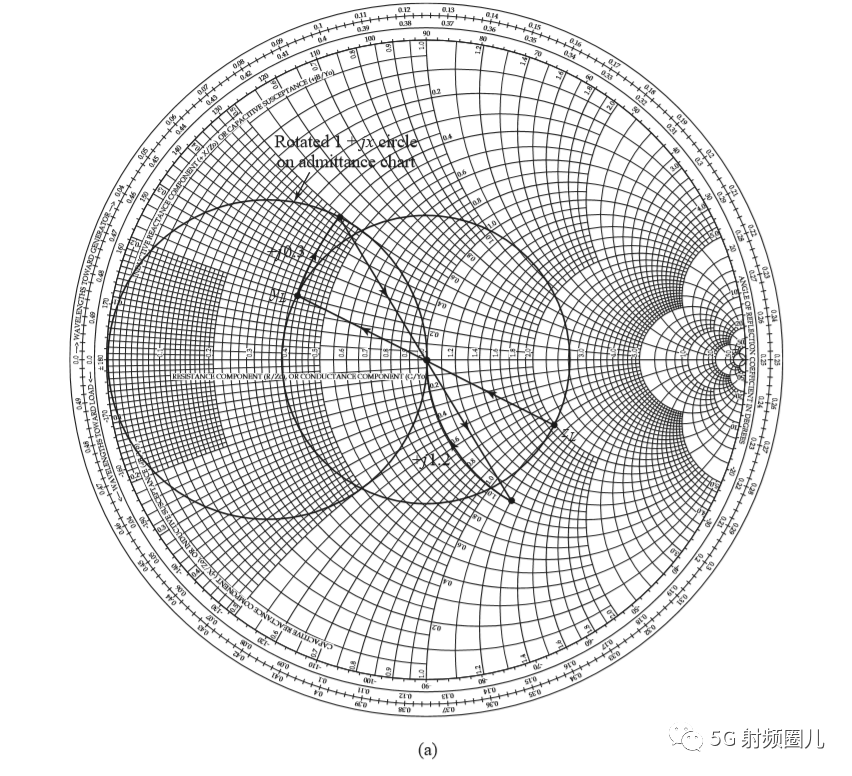
常见的L型匹配电路有两种,左L和右L,具体选择哪种,可根据源阻抗与负载阻抗的大小关系来定S( 不得不掌握的几种常见的集总参数阻抗匹配电路 )。 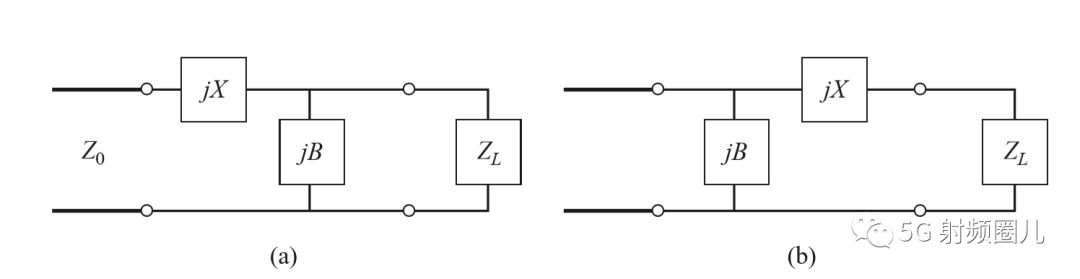 首先我们将负载阻抗ZL归一化得到zL=2-j,把这个点标注在Smith 圆图上。这个点在1+jx的圆内部,所以我们选用右L型匹配电路,或者按照我们上节学习到的规律RL>RS( 不得不掌握的几种常见的集总参数阻抗匹配电路 )。从负载看过去,第一个元件时并联电纳B,通过负载话SWR圆,且从负载过圆心画一条直线,就可以把负载阻抗转换成导纳,才能与该并联导纳相加。 我们加上这个并联导纳之后再转换回阻抗,将它画在1+jx圆上,这样我们才能加上一个串联电抗来抵消jx并与负载匹配。也就是说,这个并联电纳B能够将YL转移到Smith圆图的1+jx圆上。我们可以看到在外加一个jb=j0.3电纳之后,便能沿着等电导圆移动到y=0.4+j0.5处,再将导纳转换成相应的阻抗z=1-j1.2,在此处接上串联电抗x=j1.2就可实现匹配。使我们回到Smith圆图的中心点。 详细过程如下:
首先我们将负载阻抗ZL归一化得到zL=2-j,把这个点标注在Smith 圆图上。这个点在1+jx的圆内部,所以我们选用右L型匹配电路,或者按照我们上节学习到的规律RL>RS( 不得不掌握的几种常见的集总参数阻抗匹配电路 )。从负载看过去,第一个元件时并联电纳B,通过负载话SWR圆,且从负载过圆心画一条直线,就可以把负载阻抗转换成导纳,才能与该并联导纳相加。 我们加上这个并联导纳之后再转换回阻抗,将它画在1+jx圆上,这样我们才能加上一个串联电抗来抵消jx并与负载匹配。也就是说,这个并联电纳B能够将YL转移到Smith圆图的1+jx圆上。我们可以看到在外加一个jb=j0.3电纳之后,便能沿着等电导圆移动到y=0.4+j0.5处,再将导纳转换成相应的阻抗z=1-j1.2,在此处接上串联电抗x=j1.2就可实现匹配。使我们回到Smith圆图的中心点。 详细过程如下:
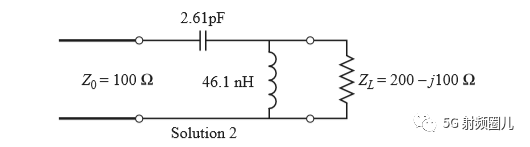
 如果该匹配电路是由一个并联电容和串联电感组成,如下图所示,在频率f=500MHz处,可求出该匹配电路的电容值和电感值。
如果该匹配电路是由一个并联电容和串联电感组成,如下图所示,在频率f=500MHz处,可求出该匹配电路的电容值和电感值。 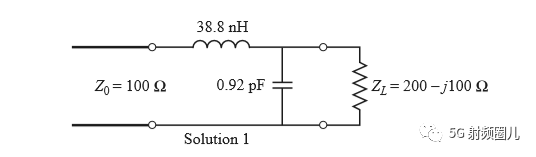
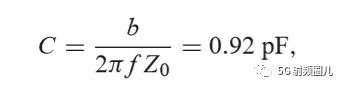
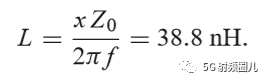 如果我们用一个b=-j0.7的并联电纳来替换之前外加的b=j0.3的并联电纳,则在移位后的1+jx圆的下班圆移动这个点到y=0.4-j0.5处,然后转换回阻抗并且加上一个x=-1,2 的串联电抗,也可以达到匹配。这时,匹配网络使一个有并联电感和串联电容来实现。在频率f=500MHz时的电感和电容值可以计算得出:
如果我们用一个b=-j0.7的并联电纳来替换之前外加的b=j0.3的并联电纳,则在移位后的1+jx圆的下班圆移动这个点到y=0.4-j0.5处,然后转换回阻抗并且加上一个x=-1,2 的串联电抗,也可以达到匹配。这时,匹配网络使一个有并联电感和串联电容来实现。在频率f=500MHz时的电感和电容值可以计算得出:
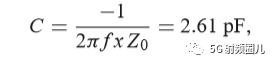
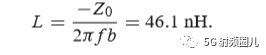 对于这两种匹配网络,其反射系数的大小与频率的关系如下图所示。
对于这两种匹配网络,其反射系数的大小与频率的关系如下图所示。 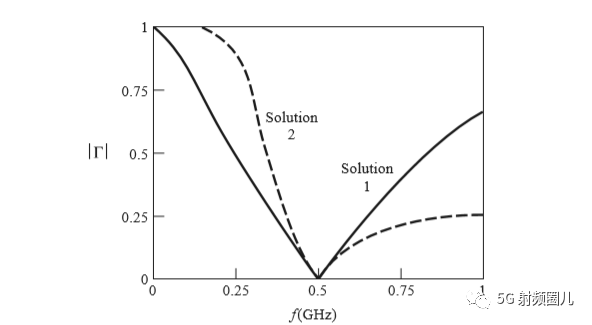 如果单纯从匹配角度来说,两种方案都可以选择,匹配带宽没有明显的区别。但是实际应用中,可以根据射频电路的需求进行选择。比如是否需要隔直?是否需要滤波?实际电感和电容的选型等等。
如果单纯从匹配角度来说,两种方案都可以选择,匹配带宽没有明显的区别。但是实际应用中,可以根据射频电路的需求进行选择。比如是否需要隔直?是否需要滤波?实际电感和电容的选型等等。
对于这个匹配问题,如果仅仅转到《 不得不掌握的几种常见的集总参数阻抗匹配电路 》 ,那么也可以直接套用公式进行求解计算。这里不再赘述。
阻抗匹配是射频设计中最常遇到的问题之一,我们慢慢把这个问题解开。
今天,我们通过几个例子来看一下,在射频设计中,如何使用Smith圆图进行阻抗匹配。例子来自于《微波工程》,今天搬出来,再学习一遍。
问题:
设计一个L型匹配网络,使其在频率500MHz处,完成负载到传输线的匹配。负载阻抗为ZL=200-j100Ω,传输线阻抗为Z0=100Ω。 这个问题的示意图如下:
 常见的L型匹配电路有两种,左L和右L,具体选择哪种,可根据源阻抗与负载阻抗的大小关系来定S( 不得不掌握的几种常见的集总参数阻抗匹配电路 )。
常见的L型匹配电路有两种,左L和右L,具体选择哪种,可根据源阻抗与负载阻抗的大小关系来定S( 不得不掌握的几种常见的集总参数阻抗匹配电路 )。  首先我们将负载阻抗ZL归一化得到zL=2-j,把这个点标注在Smith 圆图上。这个点在1+jx的圆内部,所以我们选用右L型匹配电路,或者按照我们上节学习到的规律RL>RS( 不得不掌握的几种常见的集总参数阻抗匹配电路 )。从负载看过去,第一个元件时并联电纳B,通过负载话SWR圆,且从负载过圆心画一条直线,就可以把负载阻抗转换成导纳,才能与该并联导纳相加。 我们加上这个并联导纳之后再转换回阻抗,将它画在1+jx圆上,这样我们才能加上一个串联电抗来抵消jx并与负载匹配。也就是说,这个并联电纳B能够将YL转移到Smith圆图的1+jx圆上。我们可以看到在外加一个jb=j0.3电纳之后,便能沿着等电导圆移动到y=0.4+j0.5处,再将导纳转换成相应的阻抗z=1-j1.2,在此处接上串联电抗x=j1.2就可实现匹配。使我们回到Smith圆图的中心点。 详细过程如下:
首先我们将负载阻抗ZL归一化得到zL=2-j,把这个点标注在Smith 圆图上。这个点在1+jx的圆内部,所以我们选用右L型匹配电路,或者按照我们上节学习到的规律RL>RS( 不得不掌握的几种常见的集总参数阻抗匹配电路 )。从负载看过去,第一个元件时并联电纳B,通过负载话SWR圆,且从负载过圆心画一条直线,就可以把负载阻抗转换成导纳,才能与该并联导纳相加。 我们加上这个并联导纳之后再转换回阻抗,将它画在1+jx圆上,这样我们才能加上一个串联电抗来抵消jx并与负载匹配。也就是说,这个并联电纳B能够将YL转移到Smith圆图的1+jx圆上。我们可以看到在外加一个jb=j0.3电纳之后,便能沿着等电导圆移动到y=0.4+j0.5处,再将导纳转换成相应的阻抗z=1-j1.2,在此处接上串联电抗x=j1.2就可实现匹配。使我们回到Smith圆图的中心点。 详细过程如下: 如果该匹配电路是由一个并联电容和串联电感组成,如下图所示,在频率f=500MHz处,可求出该匹配电路的电容值和电感值。
如果该匹配电路是由一个并联电容和串联电感组成,如下图所示,在频率f=500MHz处,可求出该匹配电路的电容值和电感值。 
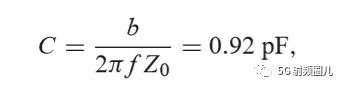
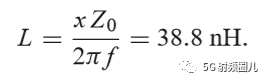 如果我们用一个b=-j0.7的并联电纳来替换之前外加的b=j0.3的并联电纳,则在移位后的1+jx圆的下班圆移动这个点到y=0.4-j0.5处,然后转换回阻抗并且加上一个x=-1,2 的串联电抗,也可以达到匹配。这时,匹配网络使一个有并联电感和串联电容来实现。在频率f=500MHz时的电感和电容值可以计算得出:
如果我们用一个b=-j0.7的并联电纳来替换之前外加的b=j0.3的并联电纳,则在移位后的1+jx圆的下班圆移动这个点到y=0.4-j0.5处,然后转换回阻抗并且加上一个x=-1,2 的串联电抗,也可以达到匹配。这时,匹配网络使一个有并联电感和串联电容来实现。在频率f=500MHz时的电感和电容值可以计算得出: 
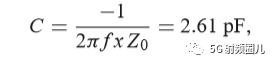
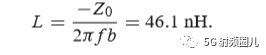 对于这两种匹配网络,其反射系数的大小与频率的关系如下图所示。
对于这两种匹配网络,其反射系数的大小与频率的关系如下图所示。  如果单纯从匹配角度来说,两种方案都可以选择,匹配带宽没有明显的区别。但是实际应用中,可以根据射频电路的需求进行选择。比如是否需要隔直?是否需要滤波?实际电感和电容的选型等等。
如果单纯从匹配角度来说,两种方案都可以选择,匹配带宽没有明显的区别。但是实际应用中,可以根据射频电路的需求进行选择。比如是否需要隔直?是否需要滤波?实际电感和电容的选型等等。 对于这个匹配问题,如果仅仅转到《 不得不掌握的几种常见的集总参数阻抗匹配电路 》 ,那么也可以直接套用公式进行求解计算。这里不再赘述。
阻抗匹配是射频设计中最常遇到的问题之一,我们慢慢把这个问题解开。


 0
0









