最近学习ADC相关资料时，“Rfilt变大引起的失真”一节中的推导涉及了向量法，虽然还记得电容的阻抗模型1/（jwc），但早忘掉它是怎么来的了，因为目前工作中很少涉及频域分析；想到公式里有个虚数就会很奇怪，所以就花了几个早晨重翻了一遍电路书。本文是相量法推导的笔记，毕竟只有明白它的推导过程，我们才能知道它的限制，才能知道什么条件下可以用这种方法简化电路分析。

首先提下正弦稳态的含义，其次以一个RC电路方程求解的过程中看下向量法的推导，从中我们就能明白这种方法的一些限制，然后我们看下三种电路元件的向量关系。最后，看下相量发的威力。

正弦稳态即电路在正弦驱动下的稳态响应。为什么是正弦呢？许多自然现象本身呈现正弦特性，如海洋表面的纹波等，正弦信号易于产生和传输；最重要的，由于傅里叶分析可把周期信号表示成一系列正弦信号之和，所以如果我们知道了如何分析正弦输入下的网络，如果电路是线性的，那么我们就能计算出电路对于任意周期信号的响应了。为什么是稳态呢？以用放大器听音乐为例，它的暂态响应最终都会消失的，刚开机听到的杂音很快就没有了，我们大体上是在研究放大器的稳态特性。因此，向量法特别适合分析如运放电路等这类线性电路，会极大得减少工作量。

下面是RC电路的求解，图片摘自电路课程的课件，为了便于自己理解会有一些细节补充。

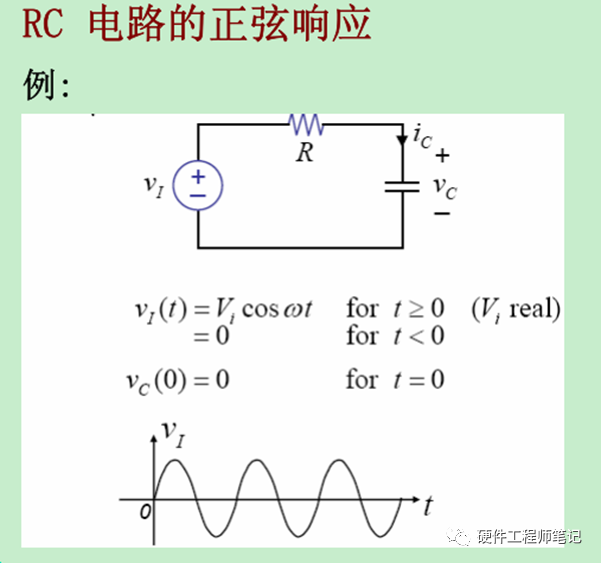
图1，待求解的RC电路，它的激励不再是简单的直流而是余弦输入。后面就会知道为什么是余弦了，因为欧拉变换。至于为啥课本上叫“正弦稳态”而不是“余弦稳态”，我想可能是正弦余弦之间很方便就可以变换吧。因为RC都是线性元件，所以电路是线性的，所以用微分方程求解时可以用“特解Vp”和“齐次解Vh”的方法，全解Vc=Vp+Vh。建立微分方程很容易，用常规方法找特解会非常复杂，会陷入到频繁的三角变换中。

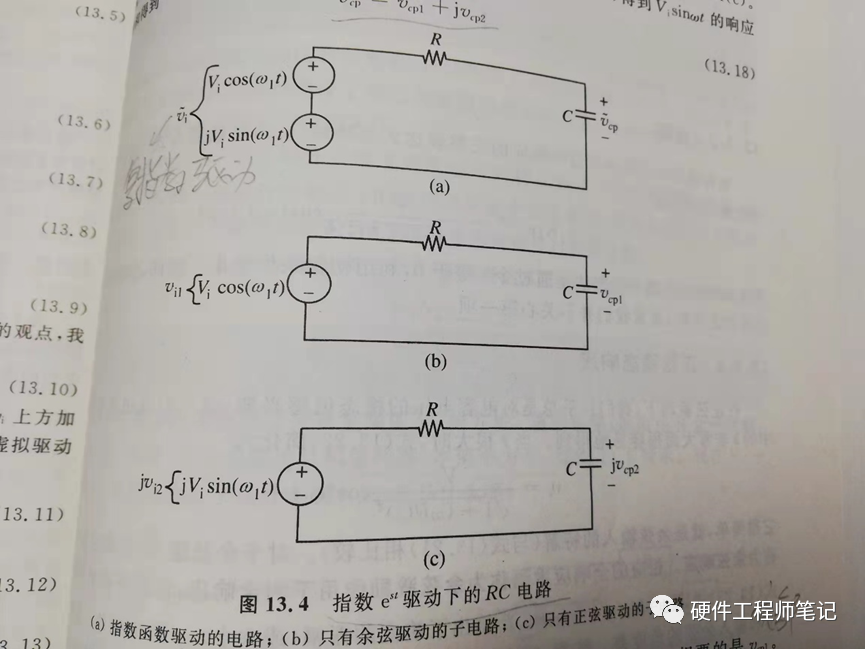
图2，我觉得这张电路图用来表示欧拉变换非常直观，同时它也说明了为什么向量法只能应用在线性线路（线性电路具有齐次性和叠加性）。

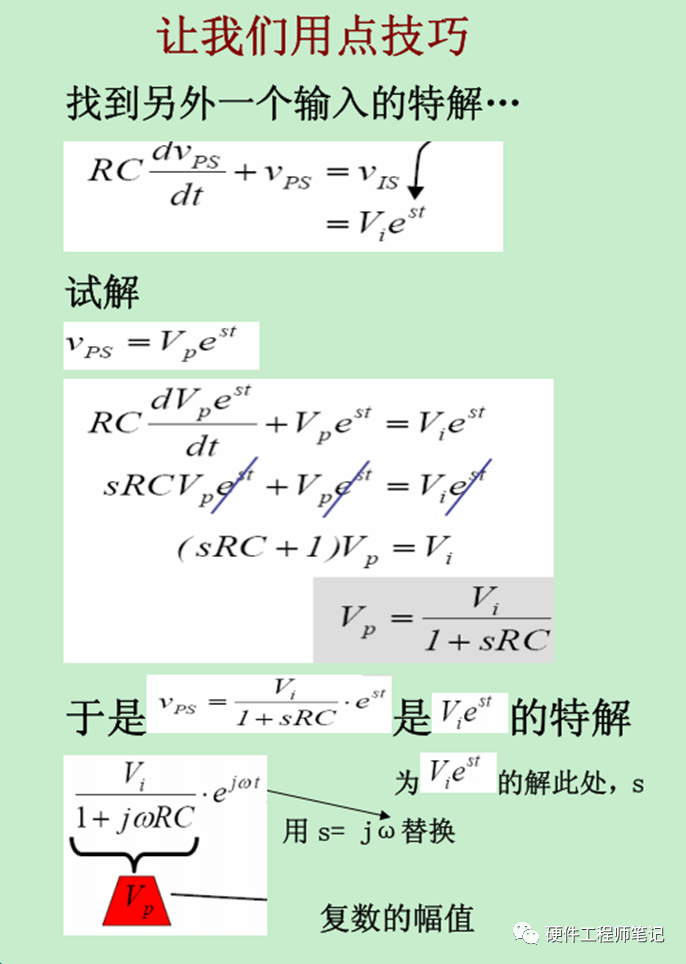
图3，用e^st代替Vicos（wt）作为输入，因为前面提过的欧拉变换，以及对指数求导非常简单。对最终的结果取实部就能找回Vicos（wt）的响应了。其实到这里就足够了，因为特解就是稳态响应，我们对这个结果也可以算出传递函数H（s）=Vi/Vp的相位和幅值；这里需要用到一些复数运算的知识。另外，e^(st)之所以能够消去，是因为t是有限制，所以它不可能是0.

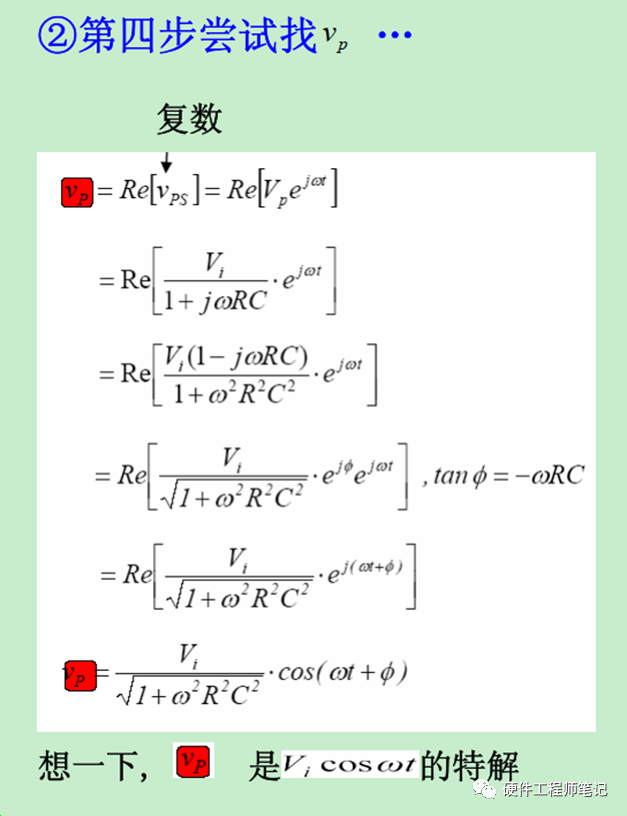
图4，回到时域，需要对结果取实部。

图5，齐次解，我们早就知道了齐次解的形式了，在一阶RC电路直流驱动时学到的。

图6，通解，或者是电路的全响应；特解是强迫响应，齐次解是自然响应。

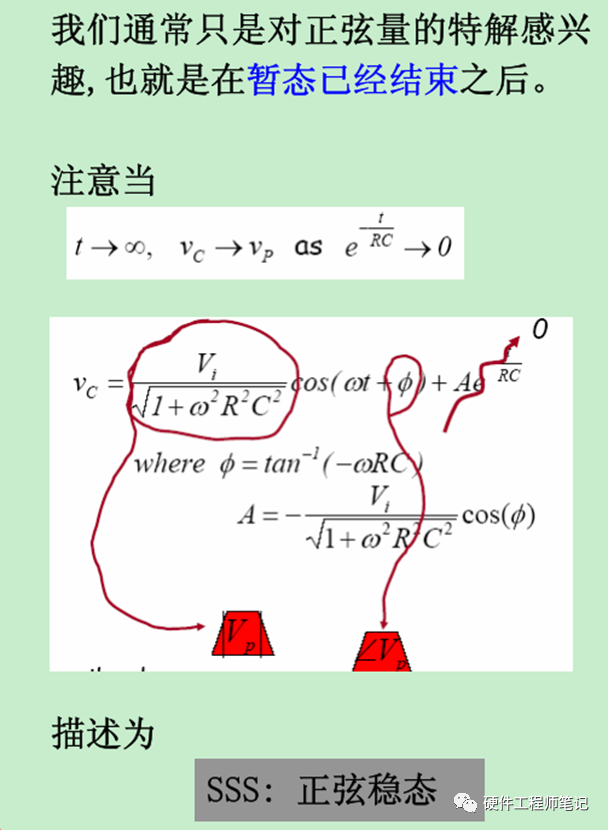
图7，全解中我们可以知道，当t趋于无穷大时，齐次解项为零，所以我们关心的稳态响应就剩下特解了。

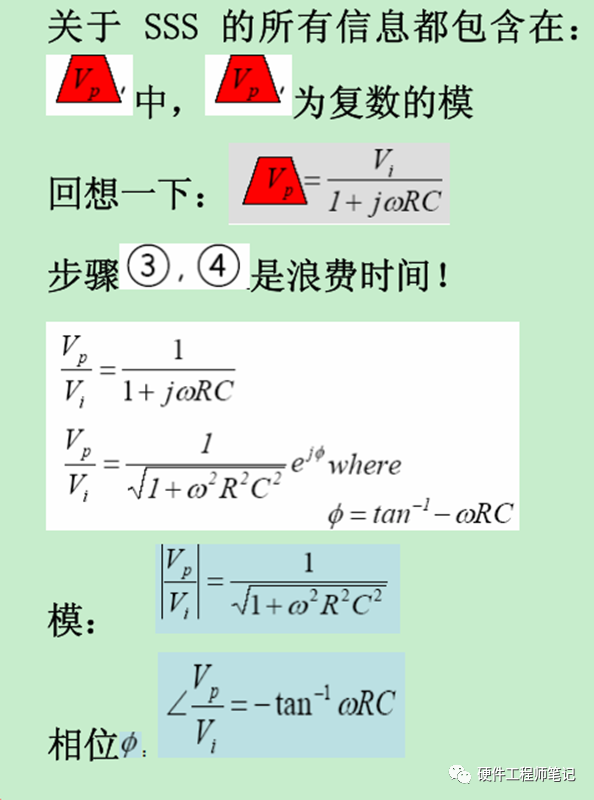
图8，这张图说明了为什么我们到第二步即图4就够了，关于正弦稳态SSS的全部信息都特解Vp中了。

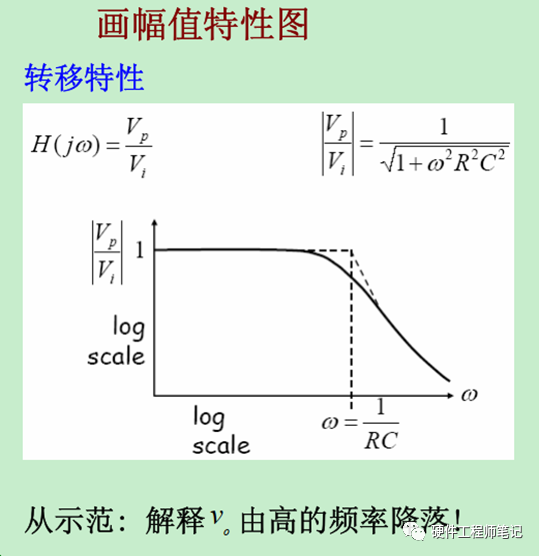
图9，幅频曲线，一个RC低通滤波器

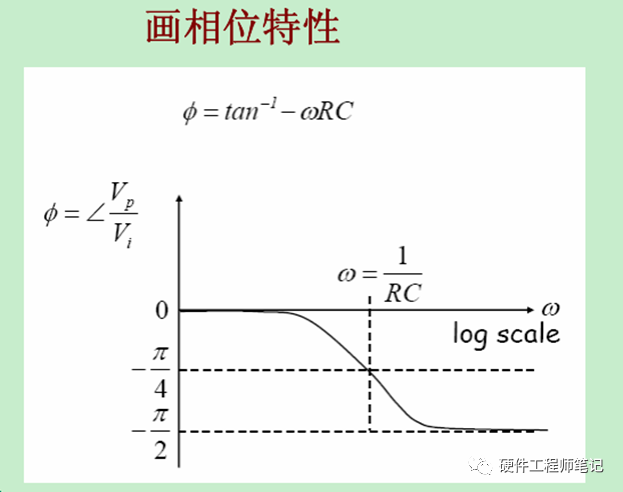
图10，相频特性，随着频率变大，输出电压的相位最多滞后输入电压90°。

上面几幅图展示了以RC电路为例的正弦稳态电路的求解过程。我们可以看到，当输入从余弦改成了指数，方程求解变得多么简单，因为指数求导就是它自己，它都被消掉了。特解就是电路的稳态响应，所以只需要两步就达到目的地。结果中出现虚数j，就是因为输入从余弦偷偷换成了指数驱动。我们对这个结果重新乘以e^(st)再取实部就能回到时域。一般不需要回到时域，我们就待在频域中也能对电路的响应有很好的理解。

关于电阻电容电感的三种电路元件的向量关系推导见图11和图12。我觉得这种推导方式还是很直观的，从我们接触最多的时域开始。电容电感元件的电流电压相位关系从中也能清楚得看出来。

图11

图12

下面我们直接用元件的电路阻抗模型，直接代入到图1中的电路，看结果是否一样吧。见图13、14。我们很轻松得就得到了和图4一样的结果，只是简单用分压公式！

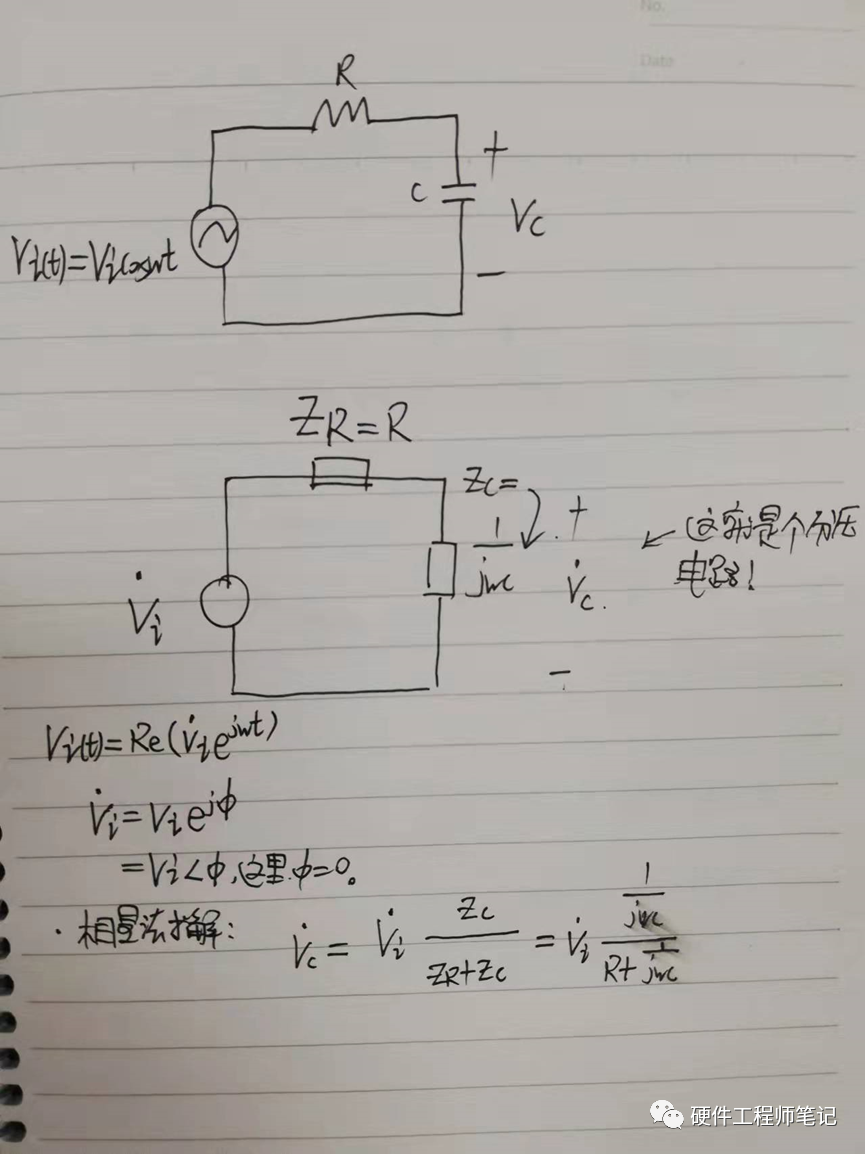
图13

图14

最后简单总结下吧。我觉得向量法推导的关键就是要记得，正弦输入偷偷替换成了指数输入即e^（st），s=jw。这是一切的开始，这么做是因为欧拉函数。所以向量法相当于应用了“逆向叠加法”（参见图2）。所以我们知道了，向量法只能用在线性电路的原因。另外，线性电路的所有简化电路的定理都可以用在阻抗电路中，如戴维南诺顿等。另外要记得最后的结果需要取实部才能回到时域，才是真实的输出，但一般不需要到这一步，只是看看频域响应如何就行了。到这里我们可以放心使用向量法了，再也不用担心虚数了。

参考资料：

电路与电子学公开课及课件

模拟和数字电路基础

电路基础