什么是串联 RLC 电路
电路一点通
455浏览
0评论
0点赞
2024-12-06
到目前为止,我们已经看到,电阻、电感和电容这三个基本无源元件在连接到正弦交流电压时,彼此之间的相位关系非常不同。但我们可以将这些无源元件连接在一起,形成一个与施加电压源串联的串联 RLC 电路。
在纯欧姆电阻中,电压波形与电流“同相”。在纯电感中,电压波形“领先”电流 90 o,表达式为:ELI。在纯电容中,电压波形“滞后”电流 90 o,表达式为:ICE。该相位差 Φ 取决于所用元件的电抗值,希望现在我们知道,如果电路元件是电阻性的,则电抗(X)为零;如果电路元件是电感性的,则电抗(X)为正;如果是电容性的,则电抗(X)为负,从而得出它们的结果阻抗为:
元件阻抗
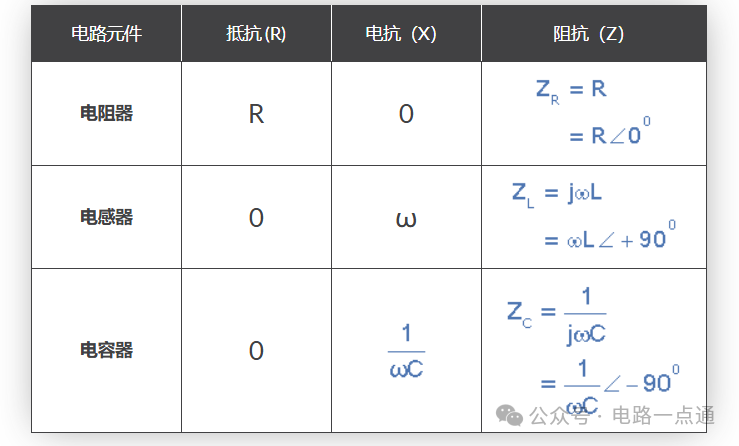
我们不必单独分析每个无源元件,而是将这三个元件组合成一个串联 RLC 电路。串联 RLC 电路的分析与我们之前研究过的双串联R L和R C电路的分析相同,只是这次我们需要考虑X L和X C的大小来找到整个电路的电抗。串联 RLC 电路被归类为二阶电路,因为它们包含两个储能元件,一个电感L和一个电容C。考虑下面的 RLC 电路。
串联 RLC 电路
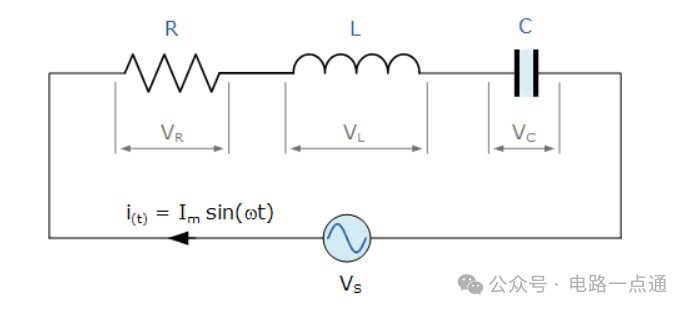
上面的串联 RLC 电路具有单个回路,流过回路的瞬时电流对于每个电路元件都是相同的。由于电感和电容电抗的X L和X C是电源频率的函数,因此串联 RLC 电路的正弦响应将随频率ƒ而变化。然后, R、L和C元件的每个电路元件上的单个电压降将彼此“异相”,定义为:
-
i (t) = I max sin(ωt)
-
纯电阻两端的瞬时电压V R与电流“同相”
-
纯电感两端的瞬时电压V L “领先”电流 90 o
-
纯电容器两端的瞬时电压V C “滞后”电流 90 o
-
因此,V L和V C相差180 度,并且互相对立。
对于上面的串联 RLC 电路,可以表示为:
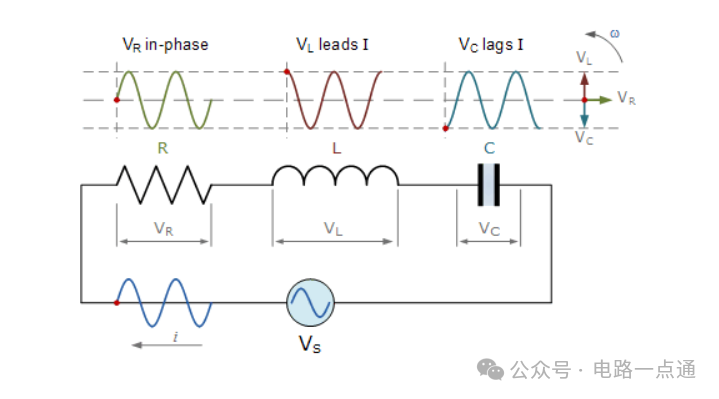
串联 RLC 电路中所有三个元件上的源电压幅度由三个单独的元件电压V R、V L和V C组成,电流为所有三个元件的共同电流。因此,矢量图将以电流矢量为参考,三个电压矢量将相对于该参考绘制,如下所示。
单独的电压矢量
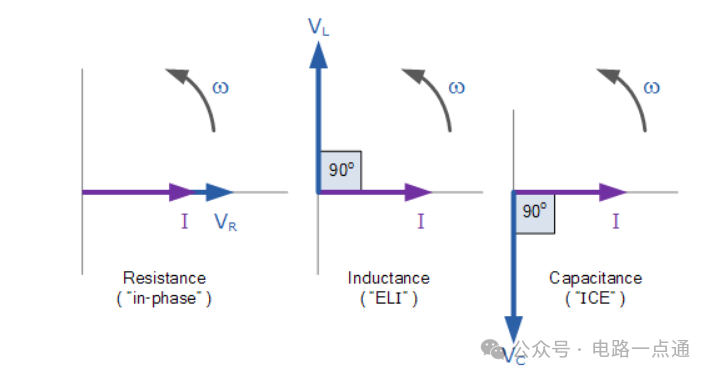
这意味着我们不能简单地将V R、V L和V C相加来求出所有三个分量的电源电压V S ,因为所有三个电压矢量相对于电流矢量指向不同的方向。因此,我们必须将三个分量电压矢量组合在一起的相量和作为电源电压V S 。基尔霍夫电压定律 ( KVL ) 适用于环路和节点电路,指出任何闭合环路周围电压降的总和等于 EMF 的总和。然后将该定律应用于这三个电压,我们将得到源电压的幅度V S as。
串联 RLC 电路的瞬时电压

串联 RLC 电路的相量图是通过将上述三个单独的相量组合在一起并将这些电压矢量相加而生成的。由于流过电路的电流是所有三个电路元件的共同电流,我们可以将其用作参考矢量,并以相应的角度绘制三个电压矢量。通过将两个矢量V L和V C相加,然后将该和添加到剩余矢量V R中,可以得到最终矢量V S 。V S和i之间得到的结果角将是电路相位角,如下所示。
串联 RLC 电路的相量图
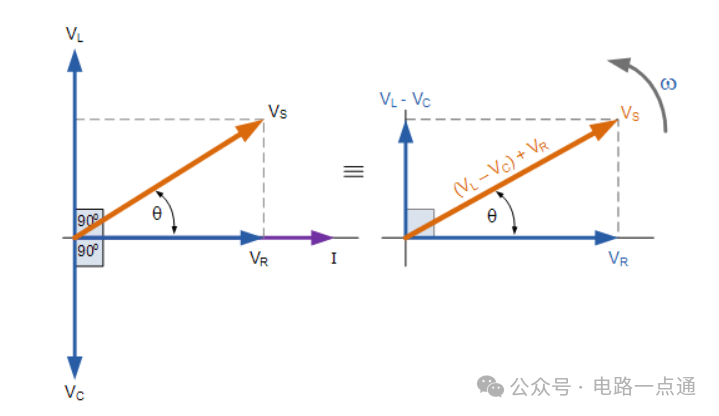
我们可以从上图右侧的相量图中看到,电压矢量形成一个矩形三角形,由斜边V S、水平轴V R和垂直轴V L – V C组成。 希望您会注意到,这形成了我们最喜欢的电压三角形,因此我们可以在这个电压三角形上使用勾股定理来数学地获得V S的值,如图所示。
串联 RLC 电路的电压三角
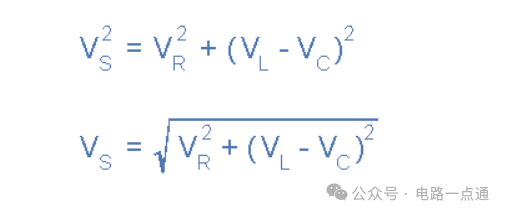
请注意,使用上述公式时,最终无功电压必须始终为正值,即最小电压必须始终从最大电压中减去,我们不能将负电压添加到V R中,因此V L – V C 或 V C – V L是正确的。最小值应从最大值中减去,否则V S的计算将不正确。从上面我们知道,串联RLC电路中所有元件中的电流具有相同的幅度和相位。那么每个元件两端的电压也可以根据流过的电流以数学方式描述,每个元件两端的电压为。

因此,我们可以看出,源电压的幅度与流过电路的电流的幅度成正比。这个比例常数称为电路的阻抗,它最终取决于电阻以及电感和电容电抗。然后,在上面的串联 RLC 电路中,可以看出,电流流动的阻力由三个分量X L、X C和R组成,其中任何串联 RLC 电路的电抗X T定义为:X T = X L – X C 或 X T = X C – X L , 以较大者为准。因此,电路的总阻抗被认为是驱动电流通过所需的电压源。
串联 RLC 电路的阻抗
由于三个矢量电压彼此异相,X L、X C和R也必须彼此“异相”,其中R、X L和X C之间的关系是这三个分量的矢量和。这将为我们提供 RLC 电路的总阻抗Z。这些电路阻抗可以绘制并用阻抗三角形表示,如下所示。
串联 RLC 电路的阻抗三角
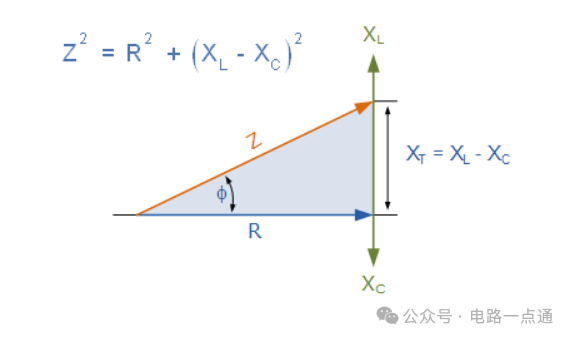
串联 RLC 电路的阻抗Z取决于角频率 ω,X L和X C也取决于角频率ω 。 如果容抗大于感抗,即X C > X L ,则整个电路电抗为容性,从而产生超前相位角。同样,如果感抗大于容抗,即X L > X C,则整个电路的电抗为感抗,从而使串联电路产生滞后相位角。如果两个电抗相同且X L = X C,则发生这种情况的角频率称为谐振频率,并产生谐振效应,我们将在另一个教程中更详细地讨论该效应。然后,电流的大小取决于施加到串联 RLC 电路的频率。当阻抗Z处于最大值时,电流最小,同样,当Z处于最小值时,电流最大。因此,上述阻抗方程可以重写为:

串联 RLC 电路示例 No1
一个串联 RLC 电路,包含一个 12Ω 电阻、一个 0.15H 电感和一个 100uF 电容,串联在 100V、50Hz 电源上。计算总电路阻抗、电路电流、功率因数并绘制电压相量图。
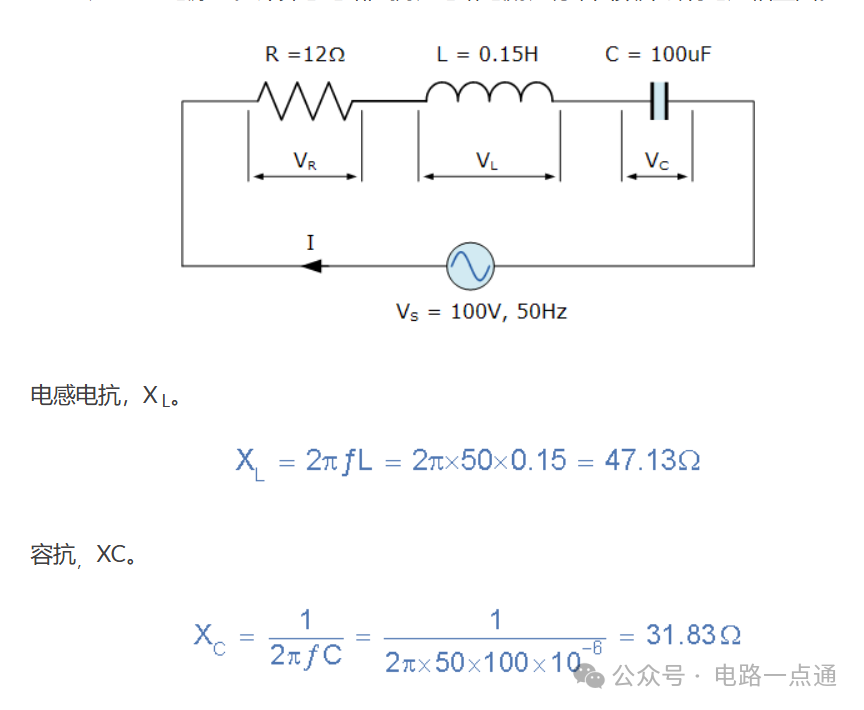

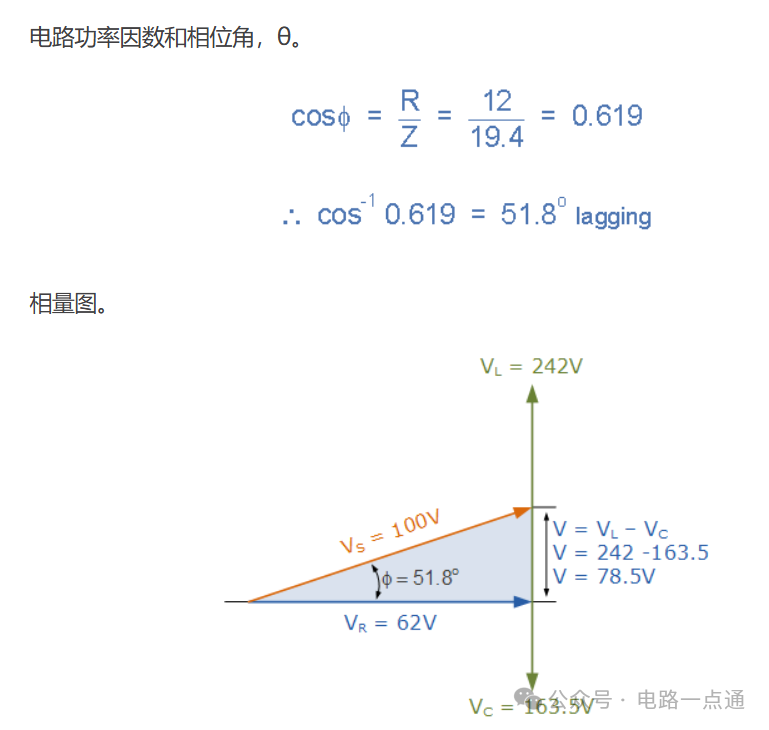
由于相位角θ计算为正值 51.8 o,因此电路的总电抗必须是电感性的。由于我们在串联 RLC 电路中将电流矢量作为参考矢量,因此电流“滞后”源电压 51.8 o,因此我们可以说相位角滞后,这由我们的助记符表达式“ELI”证实。
教程摘要
在包含电阻器、电感器和电容器的串联 RLC 电路中,源电压V S是由三个分量V R、V L和V C组成的相量和,三个分量的电流相同。由于电流是三个分量的共同电流,因此在构建电压三角形时将其用作水平参考。电路的阻抗是对电流流动的完全反对。对于串联 RLC 电路,可以通过将电压三角形的每一边除以其电流I来绘制阻抗三角形。电阻元件两端的电压降等于I*R,两个电抗元件两端的电压为I*X = I*X L – I*X C ,而源电压等于I *Z 。V S和I之间的角度将是相位角θ。当使用包含多个电阻、电容或电感(纯或非纯)的串联 RLC 电路时,它们可以全部加在一起形成单个元件。例如,所有电阻加在一起,R T = ( R 1 + R 2 + R 3 )等或所有电感L T = ( L 1 + L 2 + L 3 )等,这样,包含许多元件的电路可以轻松简化为单个阻抗。
声明: 本文转载自其它媒体或授权刊载,目的在于信息传递,并不代表本站赞同其观点和对其真实性负责,如有新闻稿件和图片作品的内容、版权以及其它问题的,请联系我们及时删除。(联系我们,邮箱:evan.li@aspencore.com )
-
本文将列出原理图和PCB设计中的常见错误,整理成一份实用的速查清单,以供参考。
-
????一、前言???? 传统离线功率转换器采用二极管-电容整流器前端时,其输入电流波形存在严重失真且谐波含
-
问 题“有一台1000kVA的老式变压器,现有负荷约200kW,如果要增加约600kW的新负载,这台变压器能否
-
电气间隙与爬电距离是电气安全设计的核心考量的参数,两者共同保障设备的绝缘性能。
-
-
esp32c2怎么实现gpio和spi方式驱动ws2812
-
-
-
-
-
-






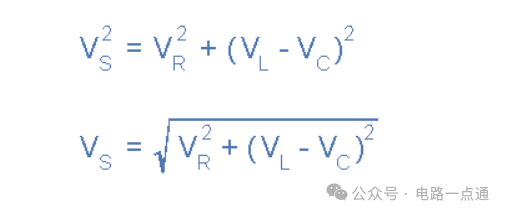









 0
0











