摘要： 以三输入判奇为例，通过对其输出函数表达式的形式变换，分别采用多种门电路及译码器、数据选择器等74 系列器件进行电路设计，给出了7 种电路实现形式，并分析了各种电路实现的优缺点。此例说明了组合逻辑电路设计的灵活性及电路实现的多样性，所采用的设计方法对其他组合逻辑电路设计具有一定的启发与指导意义。

  目前数字基础课程的实验内容包括验证性实验、综合性实验、设计性实验三部分，每一部分实验内容安排的侧重点不同。比如设计性实验的关键是设计，要求学生依据设计要求，设计合理的实验电路，并选择器件、安装调试完成实验内容。从教学实践来看，多数学生能够顺利完成实验要求，但解决问题的思路单一，设计过程灵活性差，不注意创新思维能力的锻炼。这就要求教师在合理安排实验内容的同时，不断通过各种途径，引导学生拓宽知识面，创新思维方式，对待同一问题，积极探索多种解决问题的路径。组合逻辑电路的设计多种多样，笔者选择一种奇偶校验电路实现进行详细阐述。

  奇偶校验电路在组合逻辑电路的分析与设计中具有一定的典型性和实用性，熟悉判奇电路的逻辑功能及电路实现，有助于加深对组合逻辑电路的理解与掌握。以判奇电路实现为例，分别讨论了用门电路、译码器、数据选择器的多种实现方案， 用实例说明了组合逻辑电路设计的灵活性与多样性。

  1 三输入变量判奇电路的真值表及表达式

  对于三输入变量的判奇问题， 设其输入变量分别用A、B、C 表示，输出函数用F 表示。当输入变量的取值组合中有奇数个1 时，输出函数值为1;当输入变量的取值组合中1 的个数为偶数时，输出函数值为0，依据这种逻辑关系可列写出三输入变量判奇电路的真值表如表1 所示。

  表1 三输入判奇电路的真值表

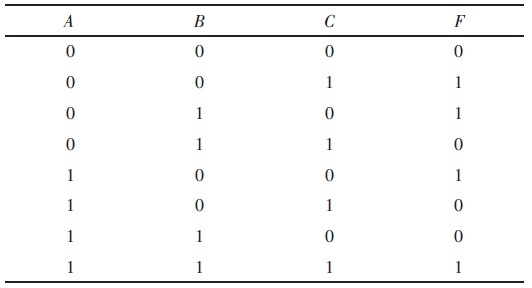
  由真值表1 可见，有4 组输入变量取值组合使输出函数值为1，即分别为。所以，三输入变量判奇逻辑问题的输出函数表达式为：

  2 采用门电路实现三输入变量判奇电路

  门电路实现三输入变量判奇电路的方法有很多， 文中列举如下。

  方法一：与或表达式（1）可用反相器、与门、或门直接实现，作其电路图如图1 所示。

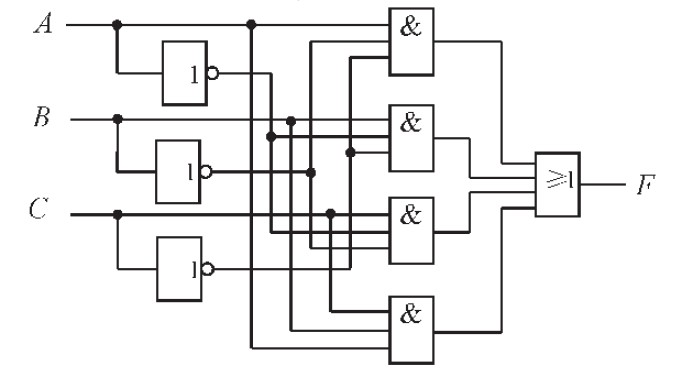
  图1 采用反相器、与门、或门实现。

  用反相器、与门、或门实现三输入判奇电路，其特点是表达式基本没有变化，实现途径简单明了，缺点是连线较多，电路复杂。

  方法二：与或表达式（1）也可用反相器、与或门实现，电路图如图2 所示。

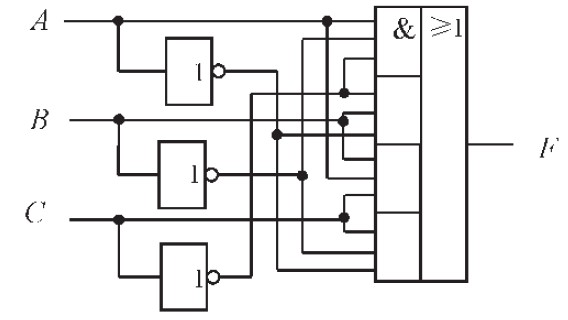
  图2 采用反相器、与或门实现

  由上述两种不同门方法实现三输入变量判奇电路可以得出，方法一和方法二虽然实现逻辑简单，但是都连线太多，浪费资源。

  同一逻辑问题的逻辑函数表达式是不具备唯一性的。对三变量输入判奇逻辑问题的输出函数表达式（1）进行变换如下所示：

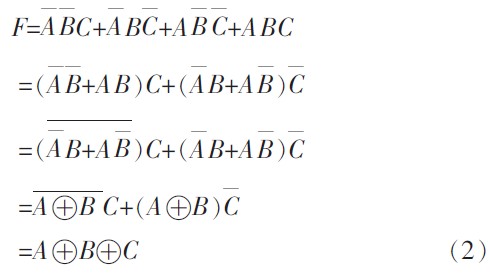
  方法三：根据上述表达式（2）得出，三输入变量判奇电路也可采用异或门实现，其电路如图3 所示。

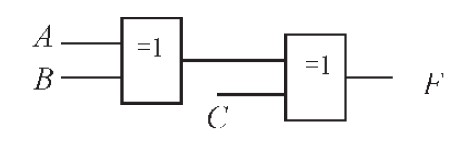
  图3 采用异或门实现

  由图3 所示电路可见，对于三输入变量判奇的逻辑问题，当采用异或门实现时，相比于方法一和方法二，电路中的连线较少，电路简单明了，实现简单。

  对于异或逻辑表达式也可以稍作变换得出：

  即一个异或门可用4 个2 输入与非门实现， 所以三输入判奇电路又可用8 个2 输入与非门实现，电路如图4 所示。

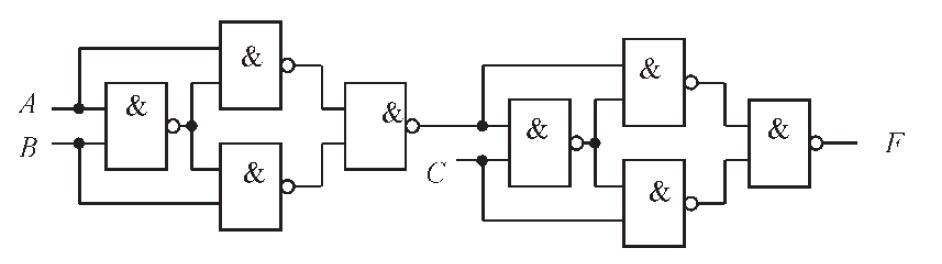
  图4 采用2 输入与非门实现

  3 采用74138 译码器实现三输入变量判奇电路

  译码器的电路结构表明，在适当的连接条件下，译码器实际上是一个最小项发生器。依据逻辑代数的基本原理，任何一个逻辑函数表达式都可以变换为最小项表达式。因此，译码器与适当的门电路结合，可以实现给定的逻辑函数。对于三输入变量的判奇问题， 利用74138 译码器并配备适当的门电路亦可实现。由74138 译码器的功能表可知：

  在（4）式中，当G1=1，G2A=G2B=0 时，有Yi=m軓i.如果把给定逻辑函数的输入变量连与74138 译码器的A2A1A0输入端相连接，比如取A2A1A0=ABC，则逻辑函数表达式（1）可变换为：

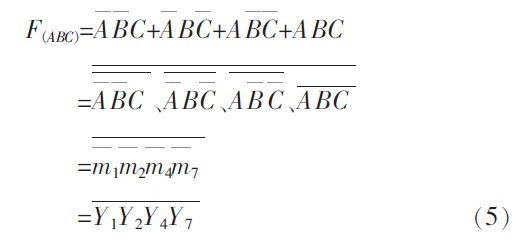
  （5）式表明，三输入变量判奇电路可以利用74138 译码器和四输入与非门实现，其电路如图5 所示。

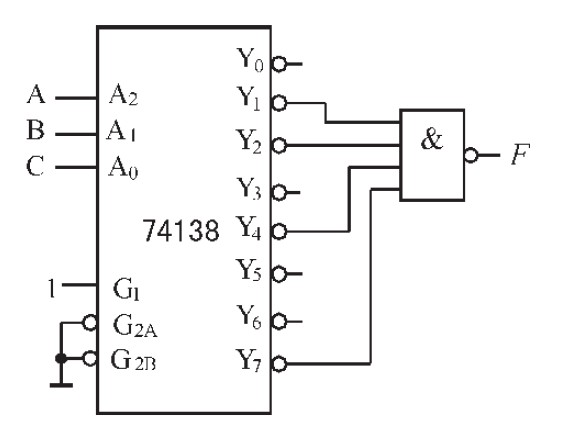
  图5 三输入判奇电路的译码器和与非门实现

  4 采用数据选择器实现三输入变量判奇电路

  数据选择器的输出与输入关系的一般表达式为：

  （式）6 中EN 是输入使能控制信号，mi是地址输入变量构成的最小项，Di表示数据输入。当使能输入信号有效时，如果把数据输入作为控制信号，则当Di= 1 时，其对应的最小项mi在表达式中出现，当Di= 0 时，其对应的最小项mi在表达式中就不出现。所以，数据选择器的输出表达式事实上是受数据输入端控制的最小项之和表达式。考虑到任何一个逻辑函数表达式都可以变换为最小项表达式，因此，只要逻辑函数的输入变量接到数据选择器的地址选择输入端，就可以实现组合逻辑函数。利用数据选择器这一特点，亦可实现三输入变量的判奇电路。

  如果选用八选一数据选择器实现三输入变量的判奇电路，此时，函数的输入变量个数与数据选择器的地址变量个数相同。如果令A2A1A0 =ABC，使能输入端接地，则（6）式变为：

  比较（1）与（7）式，可见只要D0=D3=D5=D6=0，D1=D2=D4=D7=1，则有Y=F.由此可作电路图如图6（a）所示。也可以采用四选一数据选择器实现，其电路之一如图6（b）所示。

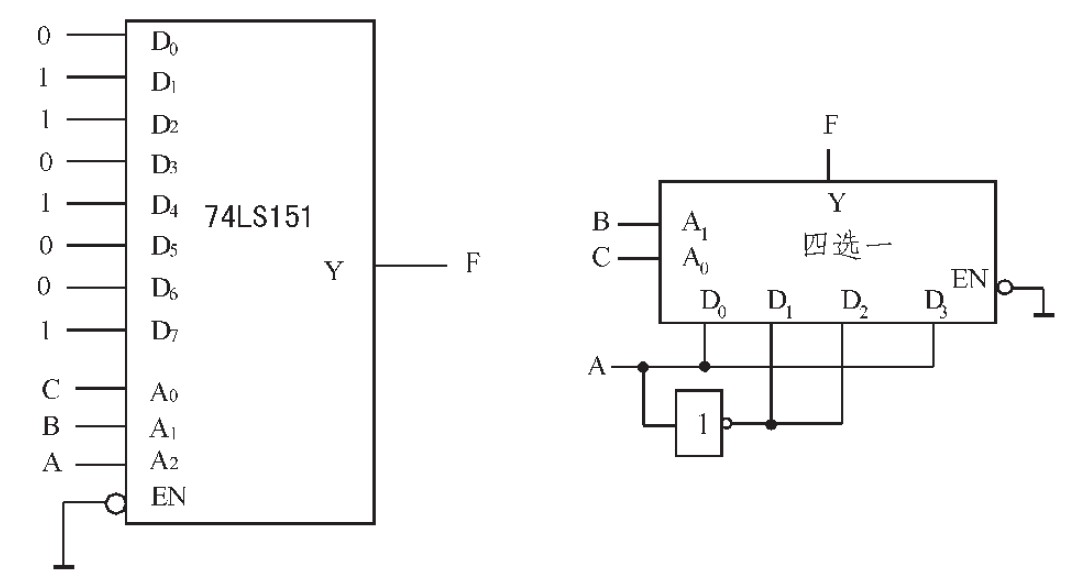
  图6 采用数据选择器实现

  5 采用反函数取非的方式设计判奇电路

  在上述的判奇中， 是按照输出函数的原函数进行分析。逻辑代数的基本定理表明：F=F ，由此可得出组合逻辑电路设计的另一途径，即先求出F軈 再反相。这样做看起来是麻烦一点，但对于某些应用场合，设计过程并不增加麻烦，反而提供了解决问题的一种途径。对于三输入变量的判奇电路，在真值表1 中对0 写出F 的反函数有：

  对式（8）两边取反有：

  对于（9）式，可采用反相器、与或非门实现，其电路如图7所示。（9）式同样可采用74138 译码器或者数据选择器实现。

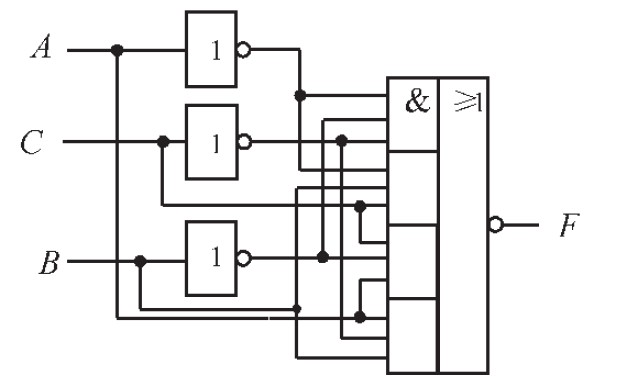
  图7 采用反相器及与或非门实现

  6 结束语

  设计性实验的关键在于设计过程， 正确的设计以熟悉基本知识为前提。对于具体的应用问题，由于组合逻辑电路元器件的多样性，为实现途径提供了多种可能的选择，文中以三输入变量的判奇逻辑问题为例， 分析讨论了多种电路实现的途径，给出了7 种电路实现方案，用实例说明了逻辑电路设计的灵活性与多样性。

  三输入变量判奇逻辑电路的设计仅仅是个例， 通过其设计途径的讨论在其他逻辑电路设计中举一反三是目的。利用文中提出的设计思路，同样可以设计全加器、全减器等其它组合逻辑电路，开阔组合逻辑电路设计的视野，培养创新思维能力，指导数字逻辑电路的设计与实验。