1.IIR滤波器的原理
1.1 概述
《数字信号处理》作为一门通信、电子、信息等本科专业基础课程,在《信号与系统》课程的基础上,学习离散信号与离散时间系统,尤其是离散傅里叶变换(DFT)和快速傅里叶变换(FFT)、数字滤波器、多速率信号处理等在通信、雷达等领域得到广泛应用。
无限脉冲相应(Infinite Impulse Response ,IIR)滤波器与(Finite Impulse Response ,FIR)滤波器构成了两种常用的数字滤波器,这两者既有联系,也有区别。
首先,IIR滤波器具有很高的滤波效率,在相同幅频响应条件下,所需的滤波器阶数明显比FIR滤波器低。其次,IIR滤波器的设计,可以借鉴模拟滤波器的设计成果。此外,IIR滤波器可以用较少的硬件资源(主要是乘加运算的DSP资源)获得较好的滤波器幅频特性。
需要注意的是,IIR滤波器的一个显著特点是不具备严格的线性相位特性,相对于FIR滤波器而言应用范围较窄,只有在不需要严格线性相位特性的情况下,可以利用IIR滤波器实现数字滤波。
数字滤波器通常由一个系统函数、差分方程、方框图或流图来表示:

其基本运算单元、方框图及流图为:
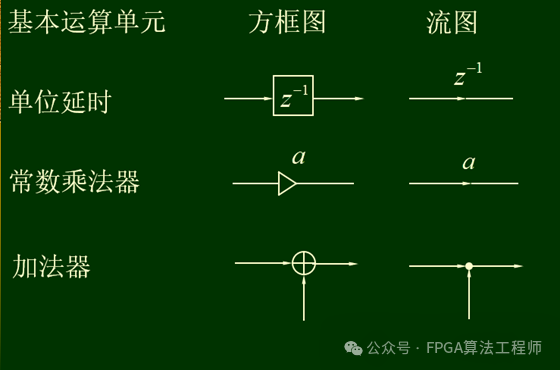
例如给定一个二阶滤波器:,则其方框图结构与流图结构如下图所示。
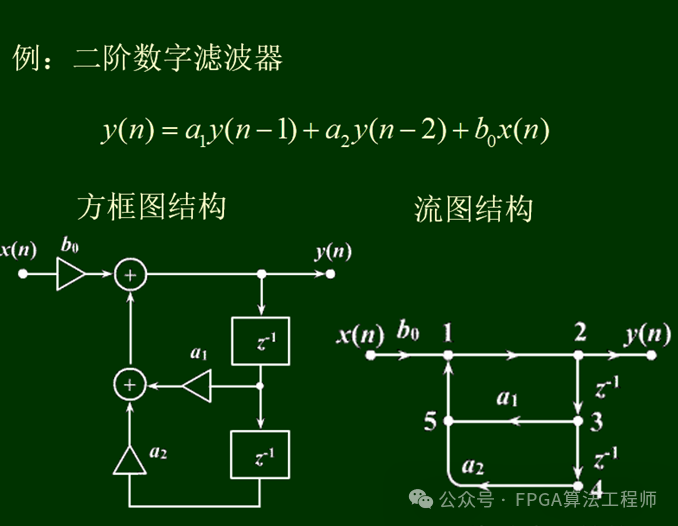
在流图结构中,我们还需要弄清楚以下几个基本概念:
-
节点:
- 源节点:只有输出、没有输入的的节点
- 阱节点(输出节点):只有输入支路而没有输出支路,它一般代表系统的输出变量,故也称为输出节点。
- 网络节点:分支节点或加法器
-
支路:只有一个输入,由一个或多个输出的节点
-
节点的值=所有输入支路的值之和
-
支路的值=支路起点处的节点值×传输系数
知乎话题:如何通俗易懂地理解FIR/IIR滤波器?
1.2IIR滤波器的原理及特性
LLR滤波器具有以下结构及特点:
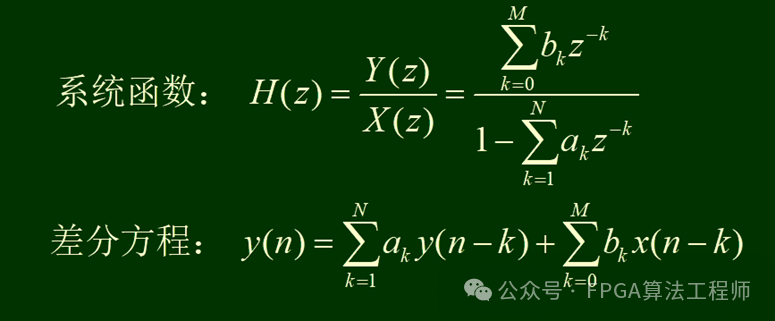
IIR滤波器的特点:
- 系统的单位抽样相应h(n)无限长 理解:由于本步骤的输出会作为下一步骤的输入,无限递归下去,所以一个时刻的影响就是无限的,也就是“无限冲激响应”。
- 系统函数H(z)在有限z平面( 0<|z|<∞)上有极点存在 LSI系统因果稳定性:一个LSI系统是因果稳定系统的必要与充分条件是系统函数H(z)必须是在从单位圆|z|=1到|z|<∞的整个z平面内(0≤|z|≤∞)收敛。即:系统函数H(z)的全部极点必须在Z平面的单位圆以内。
- 存在输出到输入的反馈,递归型结构 在物理世界的时间系统中,因环境噪声等不可控因素,IIR滤波器将可能导致所设计系统不稳定,反复递归振荡。
- 如果只有不为0,其他,则称为全极点型的IIR滤波器或自回归(AR)系统,如果由两个或多个,则称为零-极点型的IIR滤波器或自回归滑动平均(ARMA)系统。
- IIR滤波器结构:直接I型、直接II型、级联型、并联型和格型结构。
- 单位冲击相应h(n)为实数。
1.3 IIR滤波器的结构
1.3.1 直接I型
对于差分方程:如果先实现各的加权和(),再实现各的加权和(),则称之为直接I型。
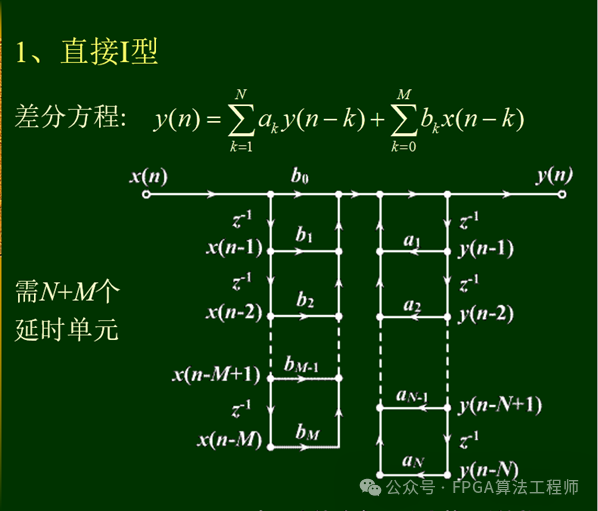
1.3.2直接II型
将直接I型结构的两个延时链子系统的次序进行交换,并将有相同输出的中间两延时链加以合并,即可得到直接II型结构(典范型结构)。
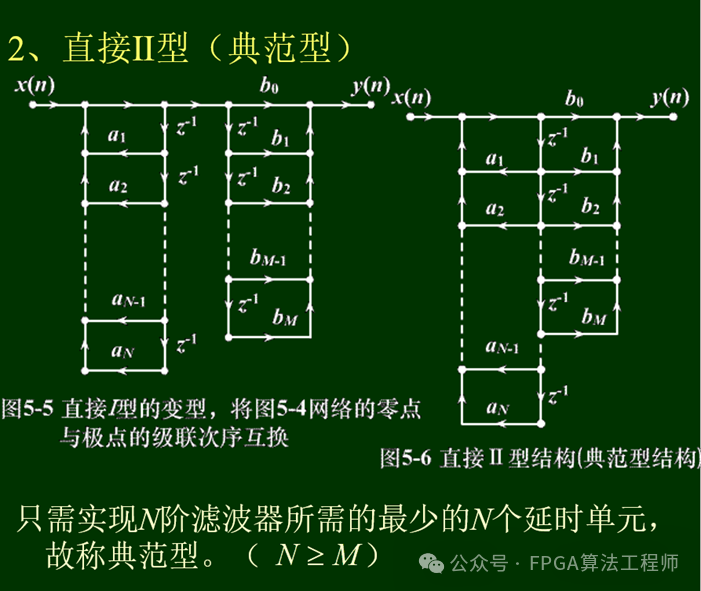
直接型的共同缺点
- 对于高阶滤波器,系数a_k和b_k分别对滤波器的极点与零点的控制作用不明显,即对频率响应的控制作用不明显,因而调整频率响应比较困难。
- 极点对系数的变化过于灵敏,易出现不稳定或较大误差
- 运算的累积误差较大:乘法运算的量化误差,造成系统输出端噪声功率大
1.3.3 级联型


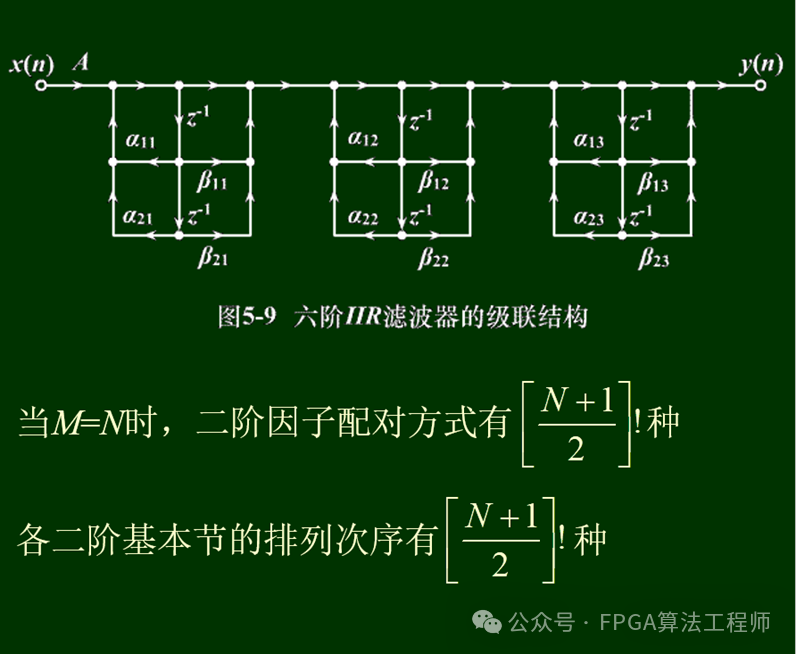

1.3.4并联型

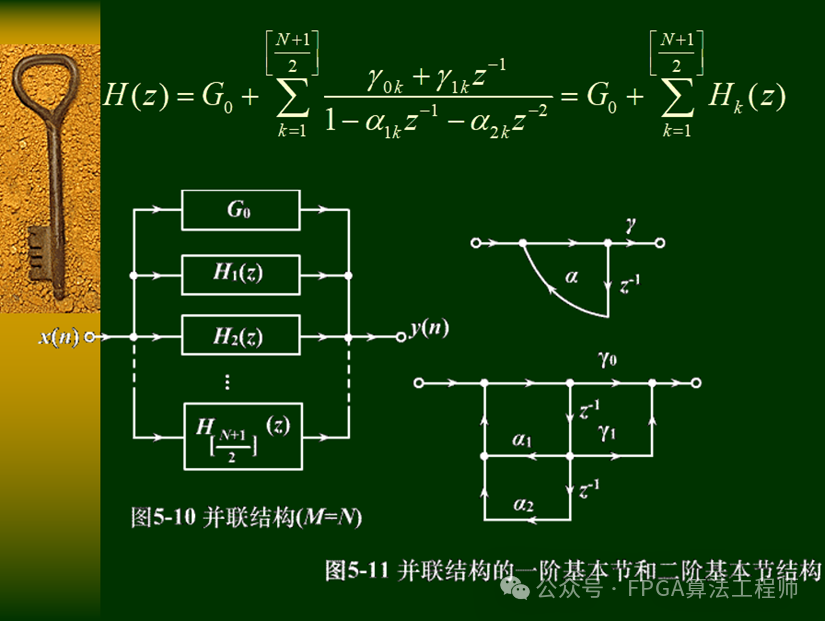
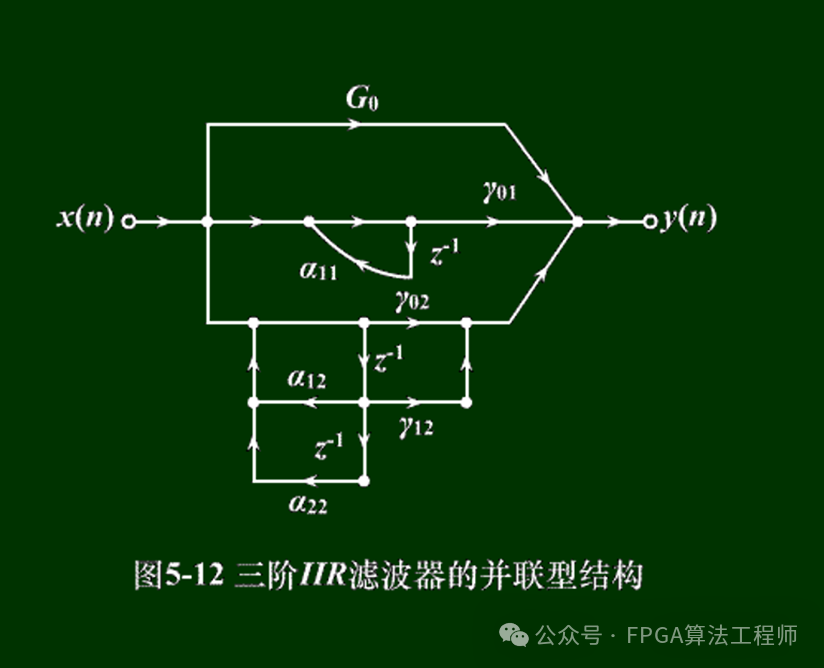

2.IIR滤波器的设计方法
程佩青《数字信号处理教程》(第四版简明版)第6章总结的IIR滤波器设计方法


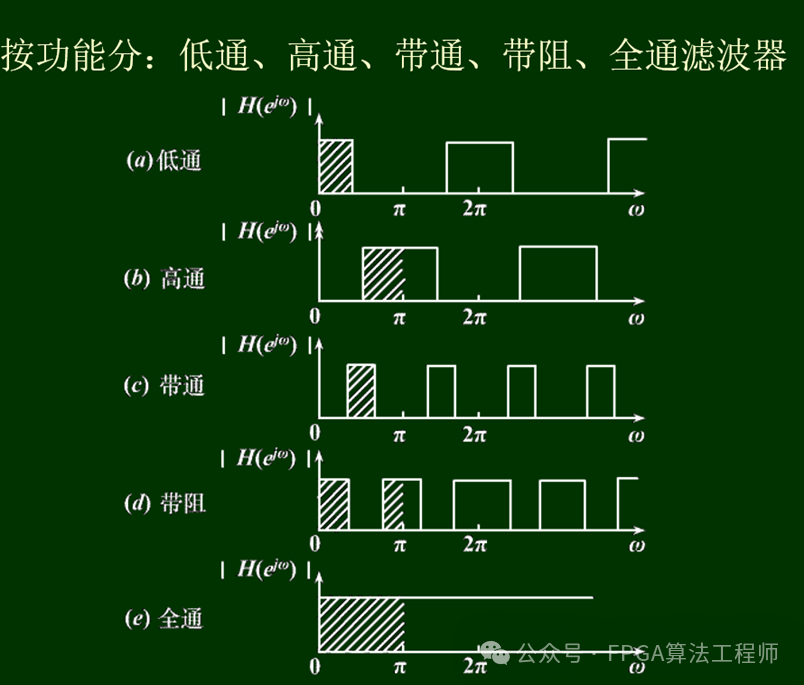









显然,在数字化时代,利用MATLAB、FPGA、DSP等软硬件来设计滤波器,才能应用到产品中!
3.IIR滤波器的MATLAB设计
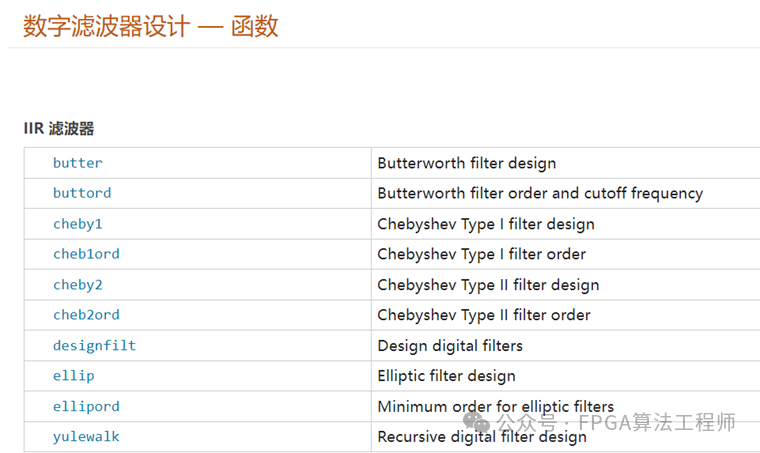
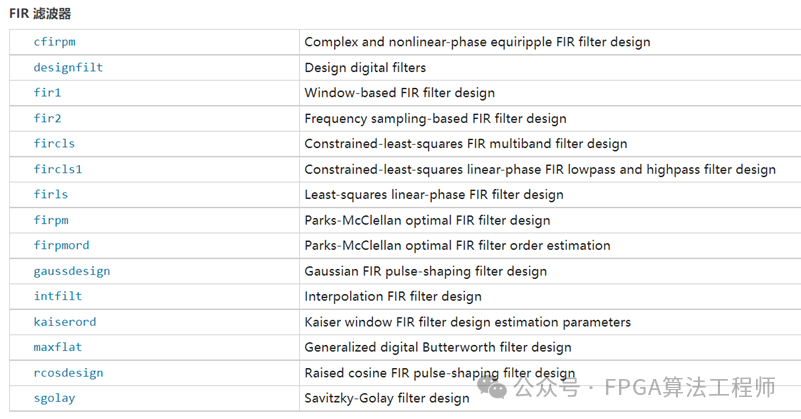
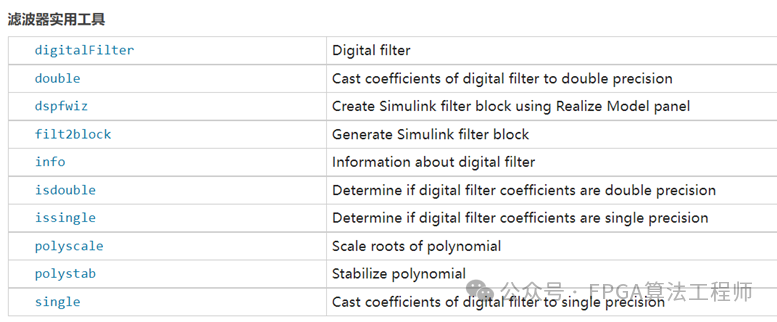
MATLAB软件提供了丰富的滤波器设计方法,例如Signal Processing Toolbox提供了FIR、IIR、单速率和多速率滤波器设计、分析和实现的案例,可以用于设计参考。
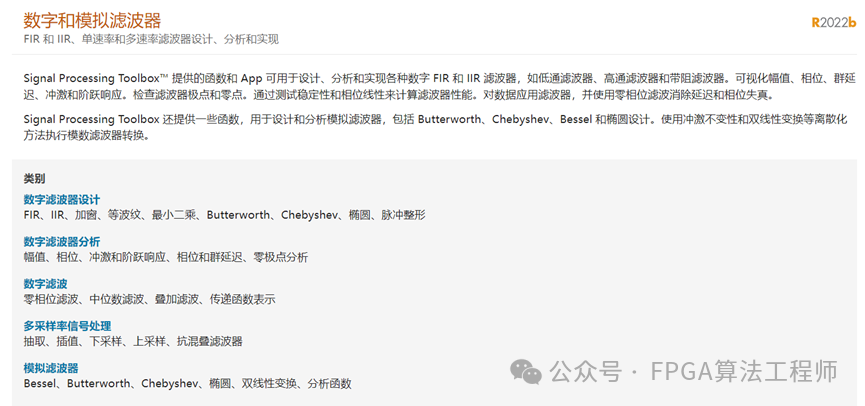

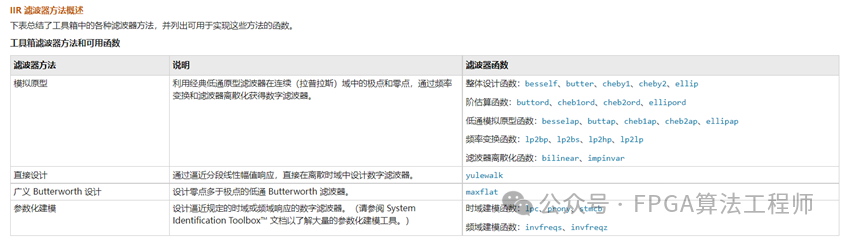
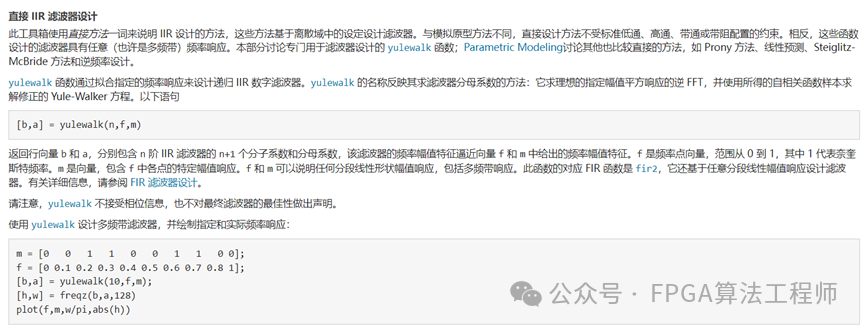
除了函数,我们也可以利用filterDesigner设计。命令行键入filterDesigner ,回车。
 进入滤波器设计界面,设计一个IIR滤波器。
进入滤波器设计界面,设计一个IIR滤波器。
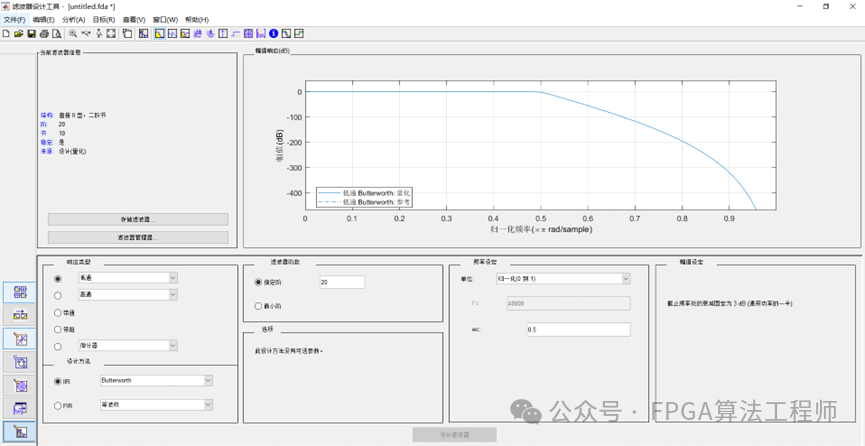
在界面的左侧,显示当前滤波器信息。“响应类型”用于指定滤波器的作用。“设计方法”包含IIR和FIR,用于指定滤波器的类型。设置滤波器的阶数,设定频率的单位可以采用归一化或Hz、kHz、MHz等。参数设置完毕,点击“设计滤波器”,可通过工具栏查看所设计滤波器的幅值响应、相位响应、群延迟响应、零极点图等。并可在左上角查看当前滤波器信息。
设计确定后,可对滤波器系数进行量化。设置量化参数,滤波器算法选择“定点”,系数字长设为16。
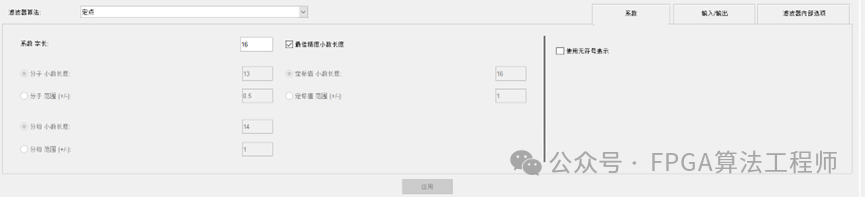
需要注意的是,在生成.coe文件时,需要满足定点、单节和直接型的FIR,才能支持Xilinx FPGA所需的.coe文件。我们也可以将所设计滤波器导出生成.m文件,以供应用。
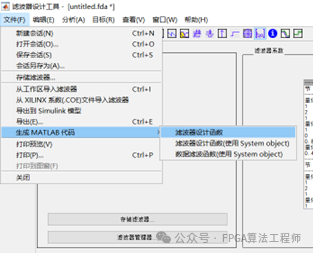
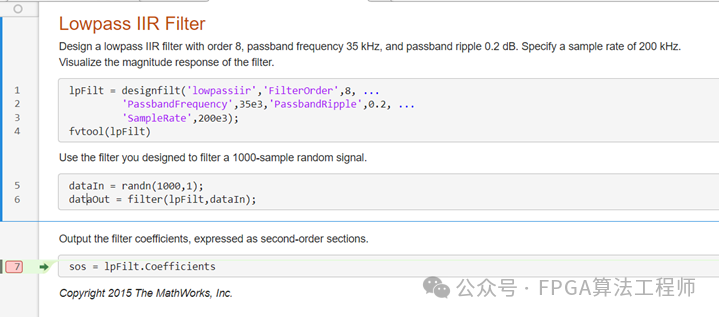
此外,我们可以应用designfilt设计滤波器,再用filter对数据进行滤波。
例如,设计一个低通IIR滤波器。
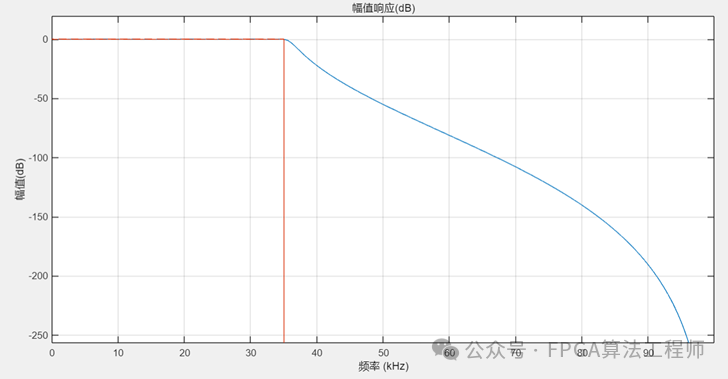
4.IIR滤波器的FPGA实现
IIR滤波器的FPGA实现比较复杂,需要应用到除法器。在利用FPGA实现IIRA滤波器前,我们需要将MATLAB设计的IIR滤波器满足设计需求后,将系数进行量化。
示例:采用cheby2函数设计一个阶数为7(级数为8)的带通滤波器,采样频率为2000Hz、截至频率为500Hz、阻带衰减为60dB,设计一个IIR滤波器。
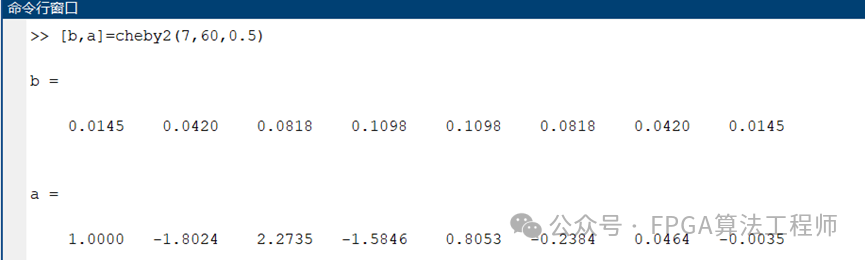
c=fvtool(b,a),将滤波器可视化。
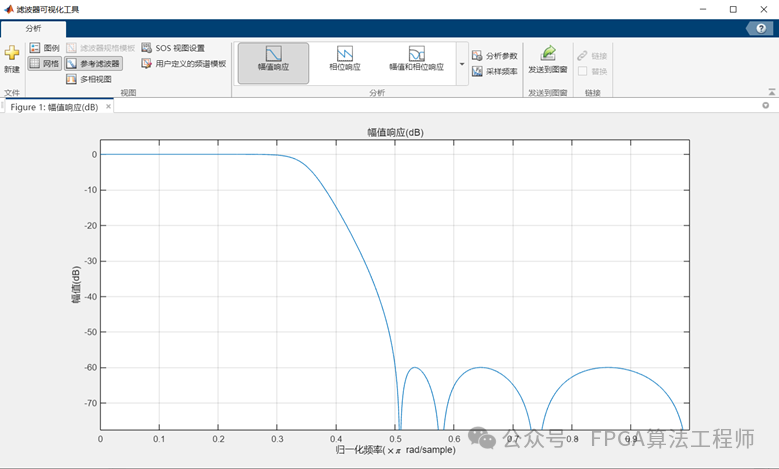
为方便FPGA实现,我们需要将系数进行量化定点。对于IIR滤波器的FPGA设计,可以参考杜勇的《数字滤波器的MATLAB与FPGA实现》第5章。在实际应用中,很少用IIR滤波器去做设计,而是更多的应用FIR滤波器设计。
最后,我们需要将处理结果进行对比,确保设计一致。
---<完>---个人博客: www.valentinefpga.cn


 0
0







