看完了控制论的传递函数一章，简单做个小回顾加深记忆。传递函数的定义可以简单看做输出除以输入，但是输入必须是脉冲函数（又叫狄拉克函数），输出也就是脉冲响应。而且系统必须是LTI即线性时不变系统才行。

传递函数是在S域的，也就是时域方程经过拉氏变换后才能得到传递函数。传递函数非常强大，实际工程项目中，一个大系统往往会分为不同个子系统，由不同工程师负责。如果每个子系统都得到了传递函数，通过把它们进行简单的相乘，就能得到总系统的传递函数了。图1.

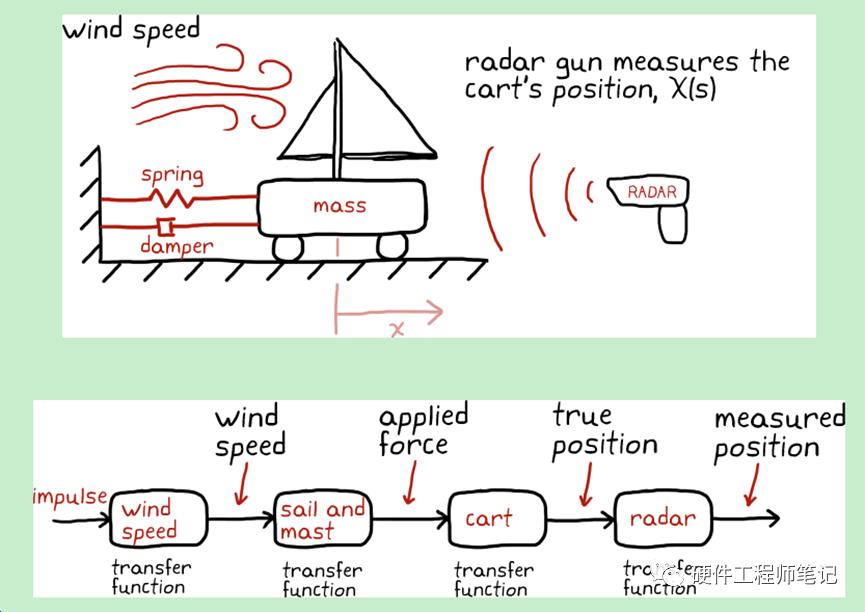
图1

在传递函数一节前介绍了很多背景知识，我们可以通过追问传递函数中一个又一个的为什么来倒着引出这些背景知识，以加深理解。首先，为什么传递函数的定义里，为什么输入必须是脉冲函数呢？脉冲函数（又叫狄拉克函数）的定义是积分为1，在一个很短暂的时间里有一个无穷大的幅值。见图2

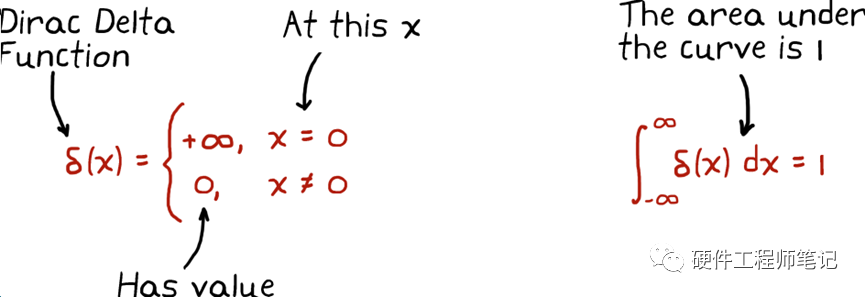
图2

对于脉冲函数和脉冲响应，书里有个非常生动的例子，见图3、图4。给一个木块施加一个脉冲函数，即快速敲打它一下，它就会跑出去了，会有一个慢慢变小的速度。

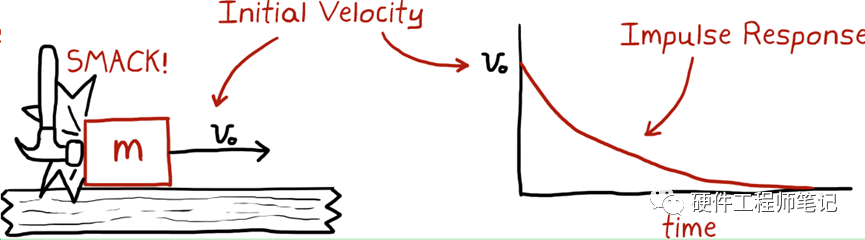
图3

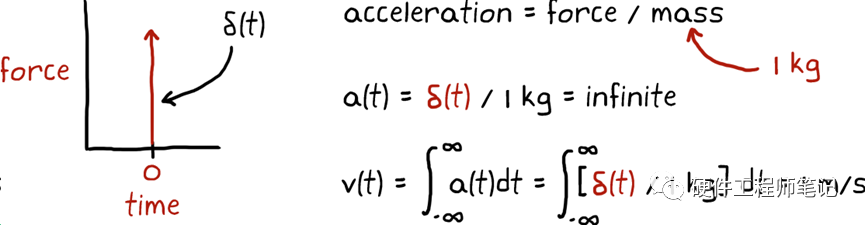
图4

脉冲函数之所以重要，是因为卷积。在LTI中，对脉冲函数进行卷积是非常方便的。我也没搞懂它的数学部分，这本书对此数学部分讨论的也很少。卷积的重要性见图6。到此，我们 已经把信号的时域响应搞定了。

图5

图6

下面从时域来到频域，它的重要性见图7

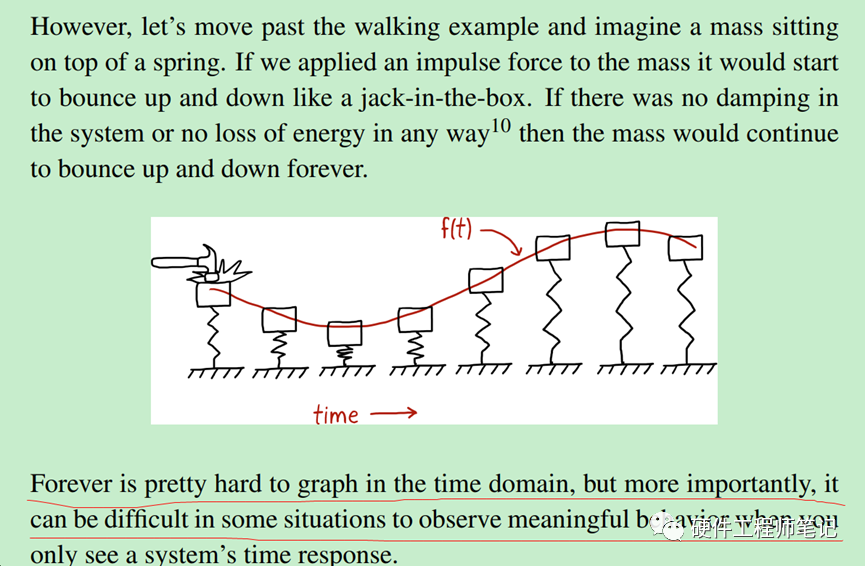
图7

关于傅里叶级数、傅里叶变换，拉普拉斯变换的数学部分，这本书没有过多讨论，我觉得这点挺好的，只专注在它的用途和物理意义上，更能便于直观理解吧。按照我简单的理解，傅里叶级数是离散的，傅里叶变换是连续的；他们都是函数从时域转换到了频域（把时域函数拆分成了正弦函数，有了频率和幅值）。见图8

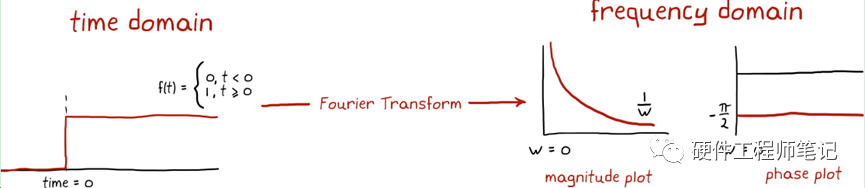
图8

更重要的是，时域的卷积，到了频域后就变成了简单的相乘！见图9，它的推导过程也不是很复杂。

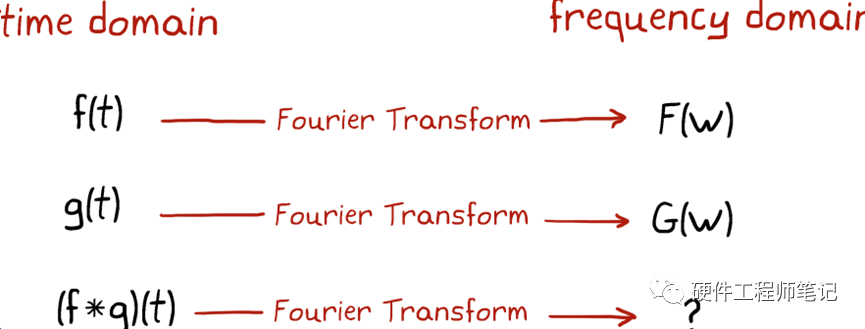
图9

而拉普拉斯变换呢，它把时域函数拆成了正弦和指数函数，而正弦和指数函数正是物理中最为常见的，所以它格外有用。同样，时域中的卷积到了S域中变成了简单的相乘。关于时域到S域的转换，我们可以通过查表搞定。工程师不应该干数学家的活。另外，傅里叶变换和拉普拉斯变换很相似的，可以从图10、11、12大概看出来。

图10

图11

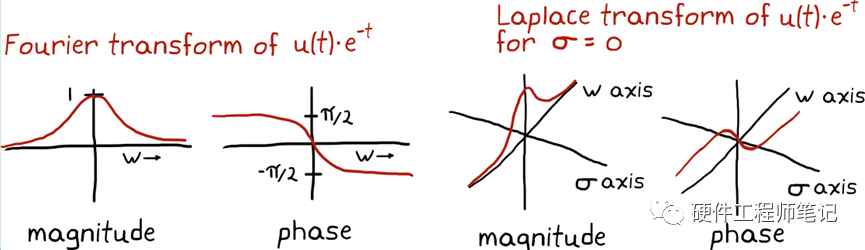
图12

这就是到达终点传递函数大概的路径了，至少我们对此有个大概的印象，传递函数把脉冲函数脉冲响应、卷积、傅里叶级数、傅里叶变换和拉普拉斯变换都串了起来。传递函数的用途在下一章节方框图中会有更详细的讲解（期待）。