本文分享串联电路、并联电路、混联电路分析、计算方面的知识，通过学习串联电路、并联电路、混联电路分析计算方面的知识，可以进一步掌握欧姆定律、电流、电压、电阻的基本概念，学会解决实际工作中所遇到的电路方面的一些简单问题。
一、串联电路分析
电阻的串联连接，就是将两个或两个以上的电阻依次首尾顺序连接，中间没有其它分支电路，只有一条通路。如下图所示的电路中，电阻 R1、R2、R3依次连接，形成串联关系，再连接到电源U上。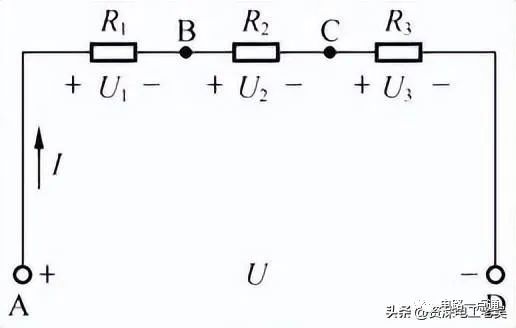
电阻串联电路1、电阻串联电路特点（1）电阻串联电路电流由于没有其它支路分流电流，所以，串联电路中流过每个电阻的电流是相等的，即：I=I1=I2=I3这就像一条没有支流的河流，在这条河流的每个位置，其流量是一样的。实际电路中，可以通过使用万用表的电流挡分别测量A、B、C、D各点的电流，其结果肯定是和上述完全一致。（2）电阻串联电路电压在串联电路的总电压，是各个电阻上的分电压之和，即：U=U1+U2+U3使用万用表电压挡分别测量AB、BC、CD和AD之间的电压，可以验证该结论成立。（3）电阻串联电路电阻将U=U1+U2+U3的两边都除以电流I，可得：U/I=U1/I+U2/I+U3/I由于I=I1=I2=I3，因此：U/I=U1/I+U2/I+U3/I=U1/I1+U2/I2+U3/I3根据欧姆定律，U/I=R、U1/I1=R1、U2/I2=R2、U3/I3=R3，因此：R=R1+R2+R3即电路的总电阻R（等效电阻），则等于各串联电阻（R1、R2、R3）之和。R称做R1、R2、R3串联的等效电阻。如下图所示，在进行电路分析时，常用等效电阻来替代一组相互连接的电阻，以利于简化电路、方便计算。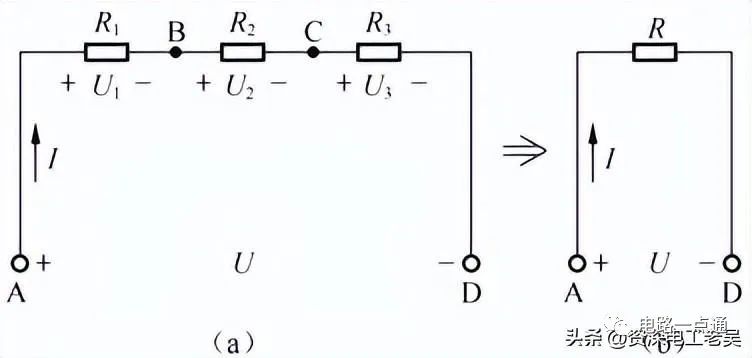
串联电阻及其等效通常电阻R1、R2…Rn串联后的等效电阻可以记作R=R1+ R2+…+Rn。电阻的串联就好比是几根水管连接在一起，每根水管就像是电阻，几根水管连接在一起，水流是从同一根水管流出，水流大小不变，只不过是水管的总长度增加了，是每根水管长度之和。（4）电阻串联电路的功率将U=U1+U2+U3同乘以电流I，得：UI=U1I+U2I+U3I由于I=I1=I2=I3、UI=PU、U1I=P1、U2I=P2、U3I=P3因此：P=P1+P2+P3所以可得: 串联电阻的总功率等于各电阻的分功率之和。（5）电阻串联电路的电压分配由于I=I1=I2=I3、I=U/R、I1=U1/R1、I2=U2/R2、I3=U3/R3所以：I=U/R=U1/R1=U2/R2=U3/R3，即：串联电路中各电阻两端的电压与各电阻的阻值成正比，电阻越大，分配的电压越大；电阻越小，分配的电压也越小。如果是两个电阻R1和R2串联，I=I1=I2、U/（R1+R2）=U1/R1=U2/R2，则:
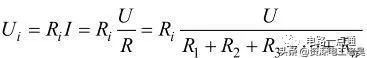
通常把上述公式称为电阻串联的分压公式。（6）电阻串联电路的功率分配由于I=I1=I2=I3，所以：
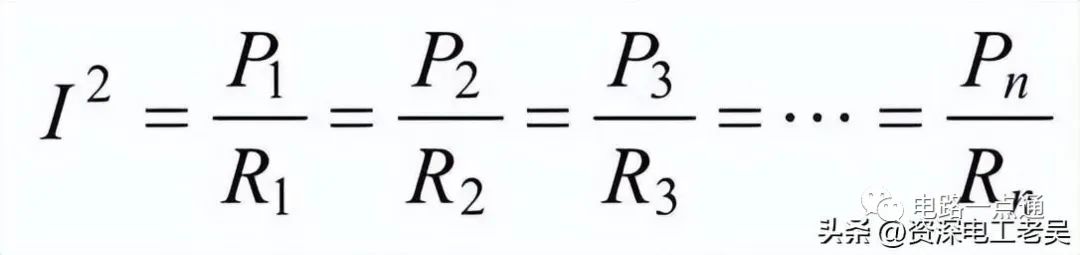
即串联电路中各电阻消耗的功率与各电阻的阻值成正比。2、电阻串联电路分析、计算实例【例1】在下图中，已知流经电阻 R1的电流为 I1=3A，试说明流经电阻 R2的电流 I2为多少？
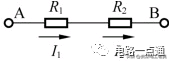
解：根据串联电路中电流处处相等得，I1=I2=3A。【例2】下图所示的电阻串联电路中，已知R1=2Ω，R2=3Ω，U2=6V，U=20V。求：（1）电路中的电流I；（2）R1和R3两端的电压；（3）电阻R3；（4）等效电阻R。
解：（1）根据欧姆定律，有I2=U2/R2=6/3=2A因为是电阻串联电路，所以I=I2=2A（2）R1两端的电压U1=R1I1=R1I=2*2=4V因为U=U1+U2+U3，所以R3两端的电压U3=U-U1-U2=20-4-6=10V电阻R3=U3/I3=10/2=5Ω等效电阻R=R1+R2+R3=2+3+5=10Ω【例3】下图 所示是常见的分压器电路。已知电路的输入电压 UAB为 220V，电位器R=200Ω，当电位器触点在中间位置时，求输出电压UCD。
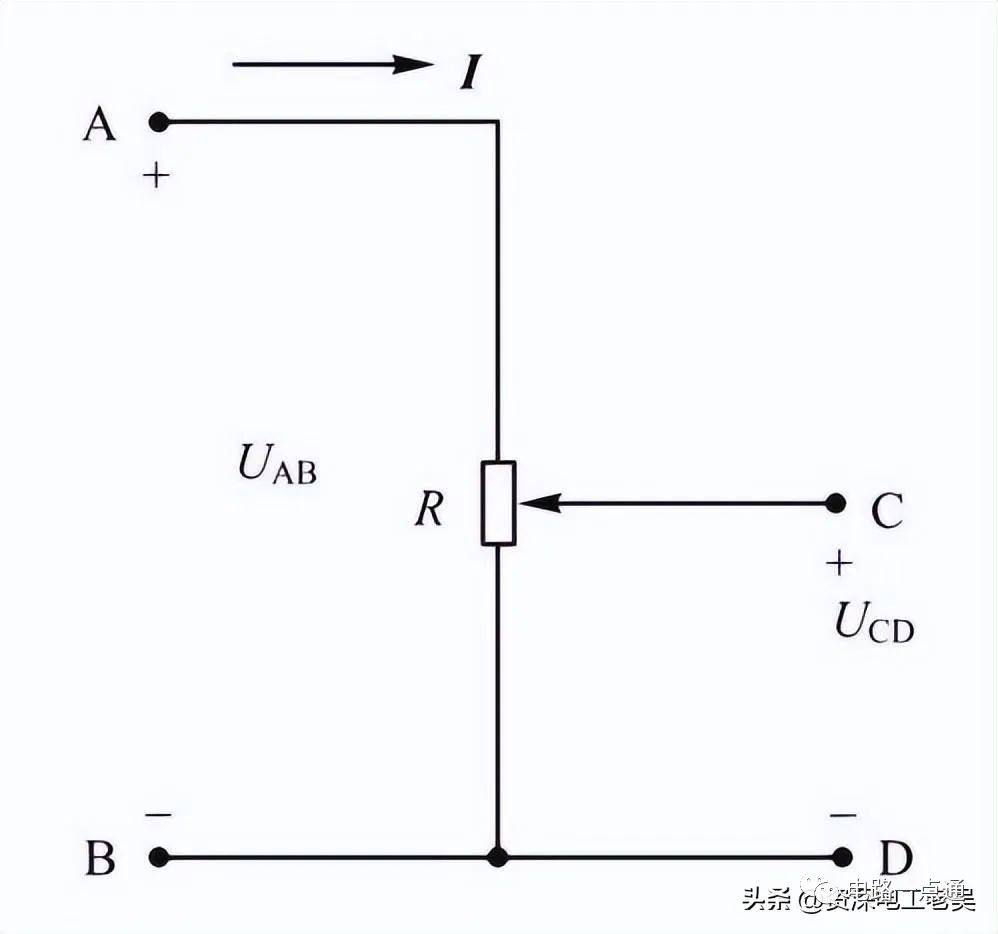
解：当电位器触点在中间位置时，上、下电阻各为 100Ω，利用分压公式即可求出输出电压，输出电压
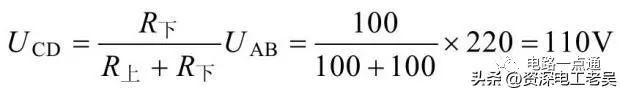
分压器为电压连续可调的分压器，当电位器触点上下移动时，输出电压UCD在0～UAB之间连续可调。--电路一点通3、电阻串联电路的应用电阻串联电路的应用十分广泛。在工程上，常利用串联电阻的方法来限制电路中的电流，如；常用的有电动机串电阻降压启动、电子电路中与二极管串联的限流电阻等；也用串联电阻的分压作用来实现一定分压要求，如用几个电阻构成分压器，使同一电源能供给不同的电压；利用串联电阻扩大电压表的量程。
二、并联电路分析电阻的并联是将若干个电阻的一端共同连接在电路的一点上，把它们的另一端共同连接在电路的另一点上，如下图（a）所示，下图（b）所示为其等效电路。
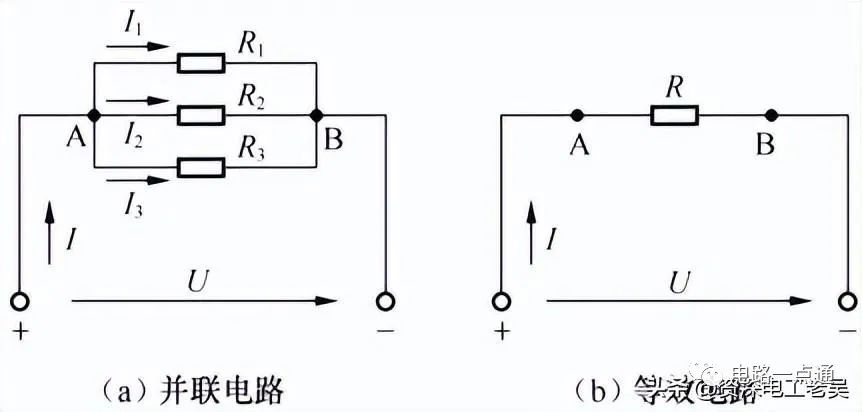电阻并联电路1、电阻并联电路特点（1）电阻并联电路电压由电阻并联的连接方式可以看出，所有并联电阻首端的电位相同、末端的电位也相同，所以并联电阻两端的电压（即电位差）相等。上图中，电阻R1、R2、R3两端的电压U1、U2、U3的关系为：U1=U2=U3＝U（2）电阻并联电路电流我们可以用万用表的电流挡分别测量通过电阻R1、R2、R3的电流I1、I2、I3以及干路电流I，可以得到：I=I1+I2+I3n个电阻并联的电路中流经第i个电阻的电流为Ii=U/Ri上这个公式可以看出：流过各并联电阻的电流与其阻值成反比，即阻值越大的电阻分配到的电流越小，阻值越小的电阻分配到的电流越大，这就是并联电路的分流原理，通常把上式叫做电阻并联的分流公式。（3）电阻并联电路电阻由上图中。可以看出：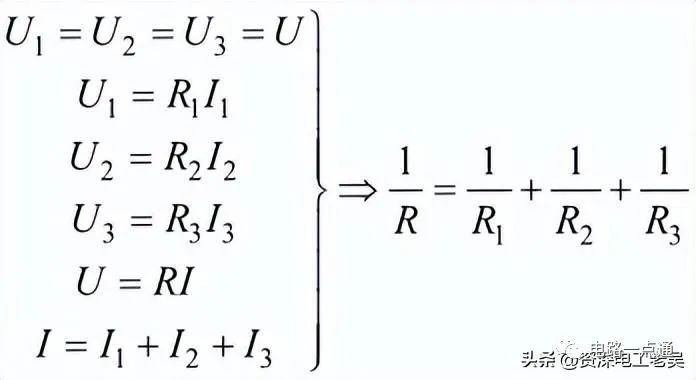
即并联电路的总电阻（等效电阻）的倒数等于各电阻的倒数之和。通常电阻R1和R2并联后的等效电阻可以记作R=R1//R2。当n个等值电阻R0并联时，其等效电阻为：R=R0/n。当二个电阻R1R2并 联时，其等效电阻为：
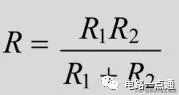
电阻的阻值越并越小，就好比是将几根水管并排在一起，这几根水管并排在一起，相当于各水管的水流叠加在一起，总的水流变大，水管阻碍水流的程度变小了。（4）电阻并联电路功率将I=I1+I2+I3同乘以电压U，得：UI=UI1+UI2+UI3，由于U1=U2=U3＝U所以根据功率定律，可得P=P1+P2+P3即并联电阻的总功率等于各电阻的分功率之和，这是串联与并联电路唯一相同之处，这也是因为能量总是守恒的，与电路的连接方式无关。（5）电阻并联电路电流分配由于U1=U2=U3＝U，所以：U=R1I1=R2I2=R3I3=IR即电路中通过各个电阻的电流，与各个电阻的阻值成反比。如果是两个电阻R1和R2并联，每个电阻所通过的电流为：
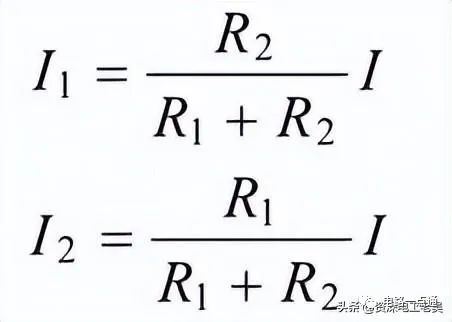
（6）电阻并联电路功率分配由于U=U1=U2=U3所以：
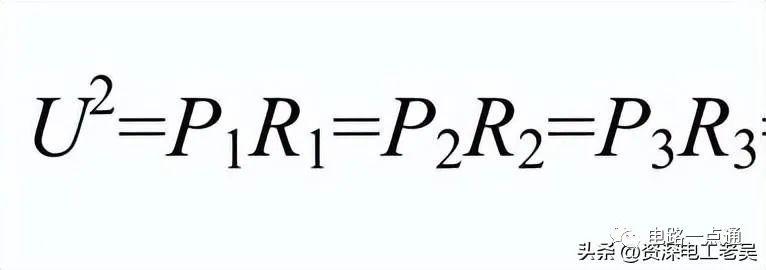
即并联电路中通过各个电阻消耗的功率与各个电阻的阻值成反比。2、电阻并联电路分析、计算实例【例1】有一个1000Ω的电阻，分别与10Ω、1000Ω、1100Ω的电阻并联，并联后的等效电阻各为多少?解：并联后的等效电阻分别为
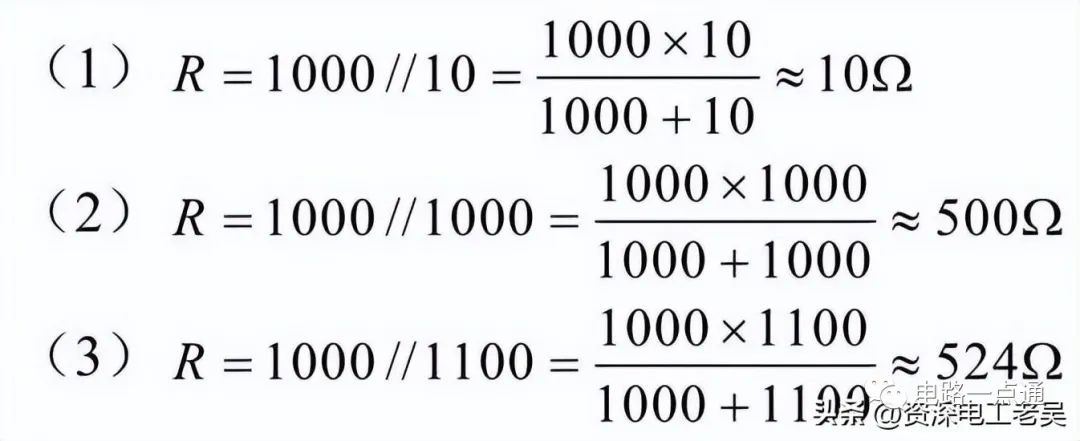
【例2】有2个白炽灯，它们的额定电压都是220V，A灯的额定功率为40W，B灯额定功率为100W，电源电压为220V。（1）将它们并联连接时，白炽灯的电阻分别为多少?它们能正常工作吗?功率分别为多少?哪一盏灯亮?（2）将它们串联连接时，白炽灯的电阻分别为多少?它们能正常工作吗?实际功率分别为多少?哪一盏灯亮?解：无论是串联还是并联，白炽灯的电阻是不变的，首先计算灯泡的电阻（1）白炽灯并联时，白炽灯的电阻分别为：
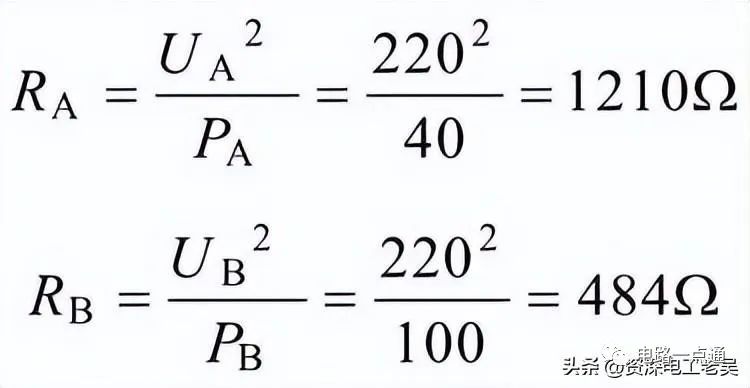
因为白炽灯在额定电压下工作，所以白炽灯并联时能正常工作，其功率分别为其额定功率，即40W和100W，100W的B灯亮。（2）白炽灯串联时，白炽灯的电阻不变，仍为RA=1210Ω，RB=484Ω，二个白炽灯的电压分别为：
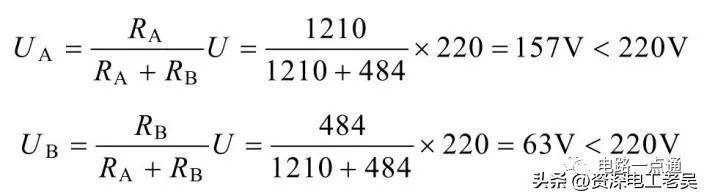
白炽灯的实际功率分别为：
因为白炽灯在串联时，不是在额定电压下工作，所以白炽灯串联时不能正常工作，其实际功率分别为20.4W和8.2W，A灯亮。3、电阻并联电路的应用电阻并联电路的应用十分广泛。在工程上，常利用并联电阻的分流作用来实现一定要求，如利用并联电阻扩大电流表的量程。同时，额定电压相同的负载几乎都采用并联，这样，既可以保证用电器在额定电压下正常工作，又能在断开或闭合某个用电器时，不影响其他用电器的正常工作。
三、混联电路的分析在实际应用中，电路中的电阻，大多不是单纯的串联或并联，而是既有串联又有并联，这种既有串联又有并联的连接方式叫做电阻的混联，如下图所示。
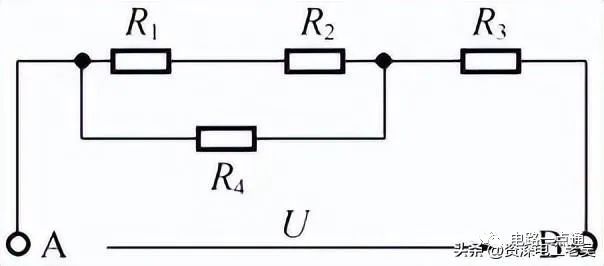
电阻混联电路对混联电路，有的比较直观，可以直接看出各电阻之间的串、并联关系，如上图中为R1与R2串联后与R4并联，再与R3串联的电路，则其等效电阻可以写为：R=（R1+R2）//R4+R3【例1】如上图所示的电阻混联电路中，已知R1=R2=2Ω，R3=4Ω，R4=4Ω，求等效电阻R。解：R=（R1+R2）//R4+R3=（2+2）//4+4=4//4+4=6Ω有的电路则比较复杂，不能直接看出各电阻之间的串、并联关系，如下图所示为电阻混联电路，可以按照以下步骤操作。
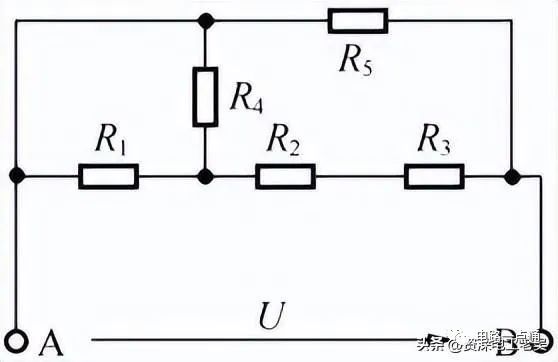
复杂的电阻混联电路① 将混联电阻分解成若干个电阻的串联、并联，根据串并联的特点进行计算，分别求出它们的等效电阻。② 用求出的等效电阻取代电路中的串联、并联电阻，得到混联电路的等效电路。③ 若等效电路中仍是混联电路，继续按照步骤②化简，以得到不含支路的等效电路。④ 根据欧姆定律、串联电路、并联电路的特点列方程进行计算。【例2】上图所示的电阻混联电路，已知R1=R4=4Ω，R2=R3=1Ω，R5=4Ω ，求等效电阻R
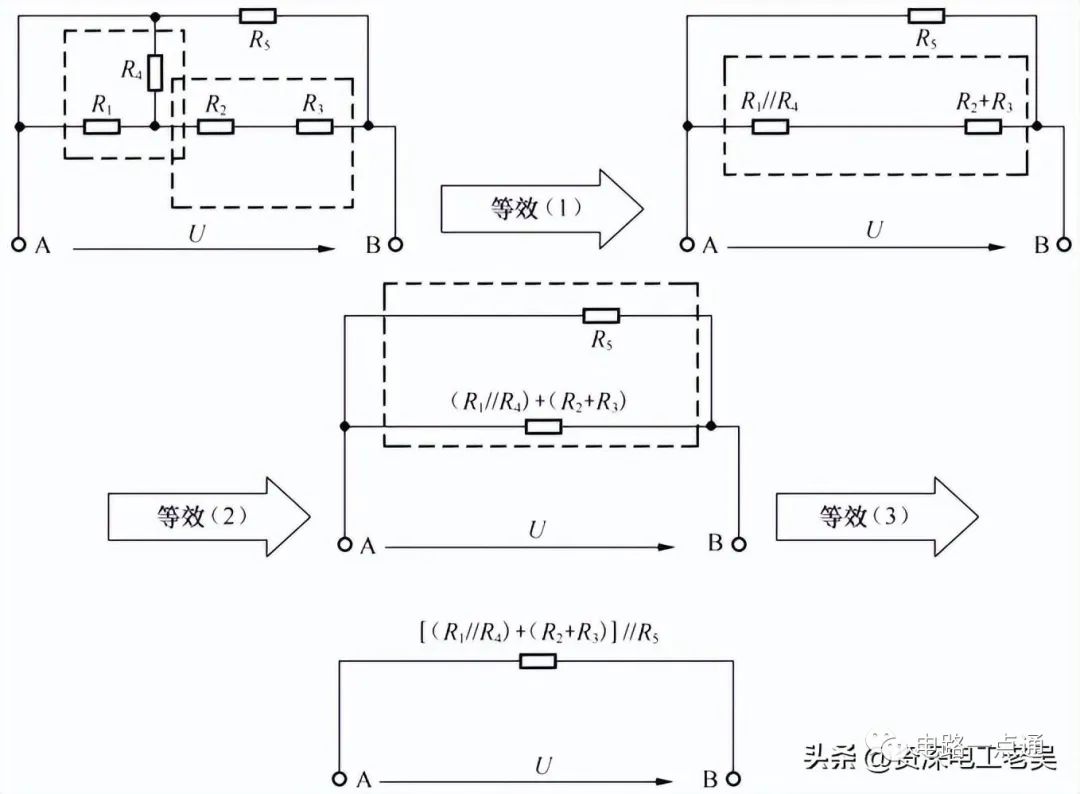
混联电路的等效变换解：（1）R1与R4为并联，其等效电阻R′=R1//R4，R′=R1R4/（R1+R4）=4*4/（4+4）=2Ω；（2）R2与R3为串联，其等效电阻R″=R2+R3，R″=1+1=2Ω。（3）R′与R″为串联，其等效电阻为R’’’=R′+ R″=2 + 2=4Ω。（4）R5与R’’’为并联，总电阻R=R5R’’’/（R5+R’’’）=4*4/（4+4）=2Ω即：总的等效电阻为R=[ ( R1//R4)+( R2+R3) ]//R5，带入得R=2Ω。
0
