刚看完了ADI三篇“接地与去耦”的相关文档，每篇文档结尾，作者都出了一道小电路题。觉得这三道题很好玩，就把求解过程都整理到这里了。先从简单的再到稍微麻烦的，就像做试卷一样，先把简单的做好，看到了一些成果，就更有信心往下做了。

一、题目1

这道题很简单，关键在于我们是否知道电容串并联的计算方法。电容串联的算法类似电阻并联，电容并联的算法类似电阻串联。三个12uF电容串联总电容为4uF。两个4uF电容并联为8uF。现在剩下的电容拓扑为，一个4uF与两个串联的8uF电容并联在一起，因此Cin为8uF。实际上，去年我设计的TIA电路就忘了这个知识点，当时的Cf由两个电容串联在一起，由于刚好算错，所以紧接着带宽也算错了，测试时才意识到。

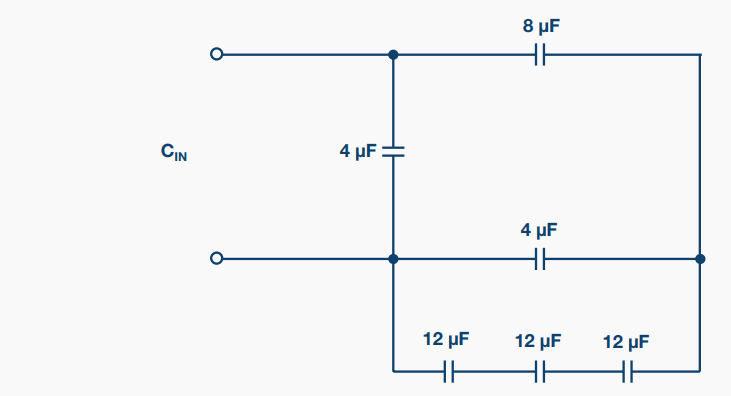
图1 心算该网络等值输入电容Cin

二、题目2

看到两个电压源，首先想到的就是叠加法。要计算1.5V提供的电流，那么只要把箭头处的节点电压计算出来即可。我们把过程图画出来，参见图3和图4。

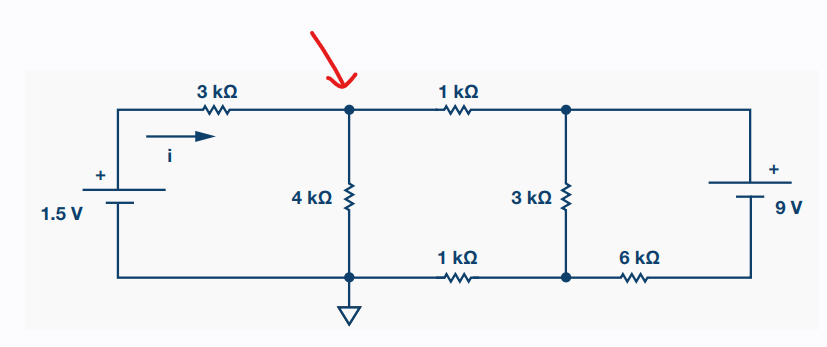
图2 1.5V需向电路提供多少电流？

先看图3，我们需要从右边往左看，9V短路后剩下R5和R7，3K我们可以看成是两个6K并联，那么现在就是3个6K并联了，等值电阻为2K。2K和两个1K串联，那么等值电阻为4K。两个4K电阻并联，等职电阻为2K。现在就是两个电阻分压了，一个3K，一个2K，所以Vo1=0.6V。仿真结果同样是0.6V，可以继续了。

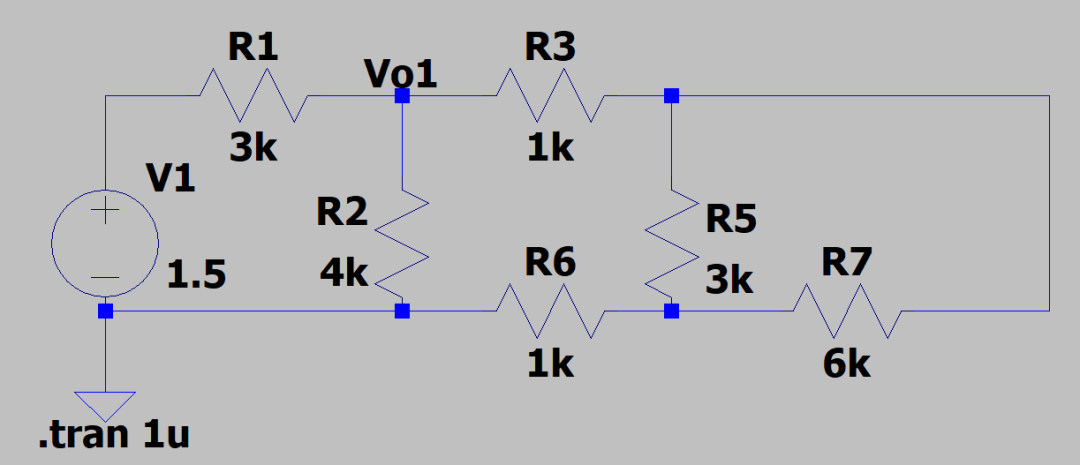
图3 9V电源置零（叠加法置零电压源就是短路，置零电流源是开路）

现在轮到求Vo2。可能我的计算方法不是最简单的，因为这次计算Vo2稍微有些麻烦了。用节点电压法，通过很繁琐的计算，最终可以得到Vo2为0.9V。跟仿真结果一样。

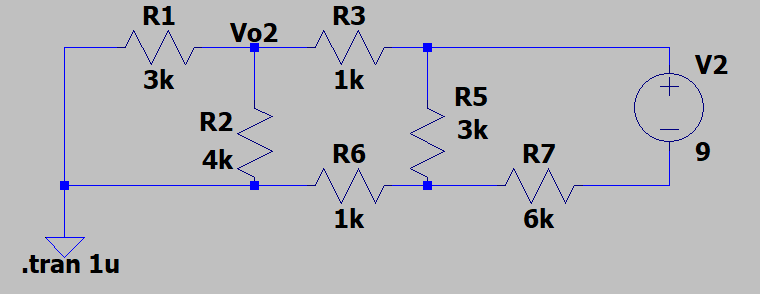
图4 1.5V电压源置零

那么Vo=Vo1+Vo2=0.6V+0.9V=1.5V，R1两边都是1.5V的话，那么R1是没有电流流过的，参见图5。因此答案为1.5V电源流出电流为0A。

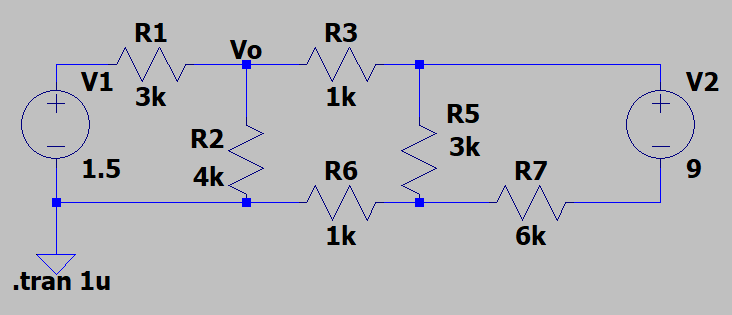
图5 总电路图

翻看作者的答案，果然，我们用的方法不是最简单的。他这里直接用的戴维南等效方法，先把右边网络化简，接下来就容易多了。关键是右边回路的戴维南等效不太常见，这次学到了。参见图6和图7。

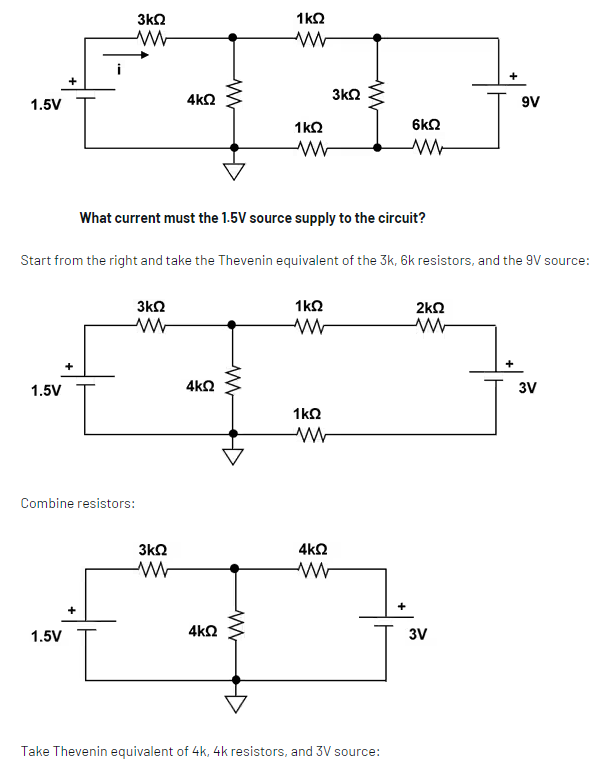
图6 原答案

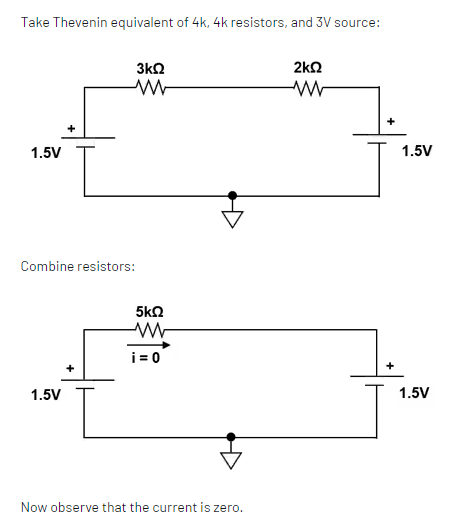
图7 原答案

三、题目3

这里是用电荷守恒定理，SAR型ADC的反冲电压就是这么计算得到的。我们只计算一个即可，先闭合S1再闭合S2，求该电容的最终电压。

闭合S1、S2之前，1uF/1V的电荷Q=CV=1uC，1uF/3V的电荷Q=CV=3uC，2uF/6V的电荷Q=CV=12uC。

先闭合S1，那么总电荷Q=4uC，电容并联后为2uF，所以这部分电容电压为V=Q/C=4/2=2V。

再闭合S2，那么总电荷Q=4+12=16uC，电容并联后为4uF，所以该电容总电压为V=Q/C=16/4=4V。

实际上这里跟开关闭合顺序是没有关系的，电容最终电压总是4V。这里假设了电容是理想的，无损耗。

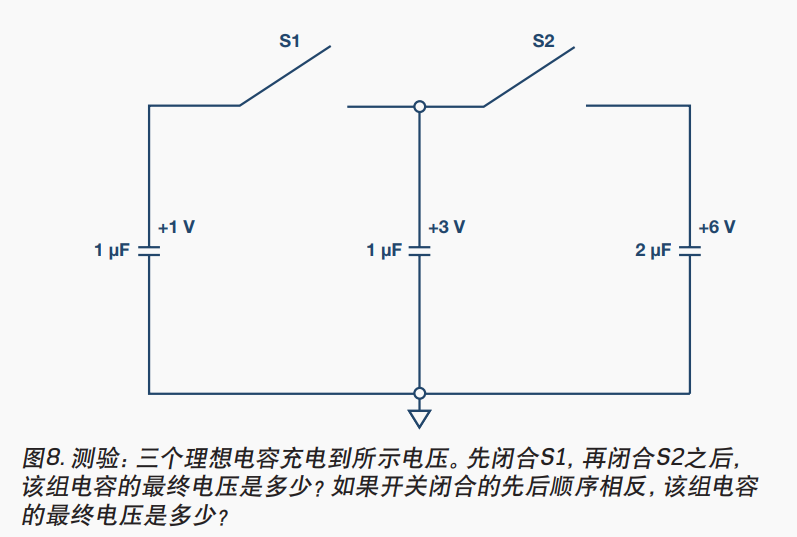
图8 题目3

四、总结

这三道题都核对过答案了，没有问题。第二道题我们的解法没有答案更简洁，虽然结果没有问题。从答案中学到了遇到电压源电阻网络，其实都可以先考虑戴维南等效，看是否可以简化计算。