为VCM的BUCK变换器做控制器的补偿时,需要用TYPE3补偿器,要用双零点补偿功率级的控制到输出函数中存在LC滤波器的双极点。那么问题就来了,在s域用运放很容易的实现TYPE3的效果,如果要把控制器改为数字控制,那么3P3Z又该如何实现呢?
本文以一个VCM的BUCK变换器作为例子,根据BUCK变换器的电感和电容等参数,迅速的得到3P3Z补偿器所需的零极点频率的位置。根据bode图观察频域的效果,接着离散到Z域,然后编写差分方程的3P3Z程序,在PSIM里面进行仿真。如果觉得好用,就可以很容易的应用在LLC或其它电压控制模式的拓扑中。
先在matlab里面建立3P3Z的s域传递函数。
%时间:2018年1月22日
%BUCK VCM 3P3Z Control
%By:Maileyang
clear all;
echo off
clc
%输入参数:
Vin = 12; %12V
Vo = 5;
Io = 20; %25A
Lf = 10e-6; %BUCK储能电感
Co = 470e-6; %Cout 电容
Resr = 2e-3; %esr电阻
fsw = 100e3; %fsw = 100Khz
Rload = (Vo/Io);
%计算电压模式控制到输出的传递函数
gxnum = Vin*[Resr*Co 1];
gxden = [Lf*Co*(1 + Resr/Rload) (Resr*Co + Lf/Rload) 1];
Hs = tf(gxnum, gxden);
zpk(Hs);
Hs = (Hs);
%控制器的参数部分
%输入参数
flc = 1/(2*pi*sqrt(Lf*Co)); %VM BUCK LC滤波器转折频率
fesr = 1/(2*pi*Co*Resr); %输出电容的esr引起的零点在30KHZ
fp0 = 2000; %零点处极点频率,决定系统低频增益
kfp = 0.15; %两高频极点频率之间的距离
kfz = 1.05; %两低频零点频率之间的距离
wz1 = flc * 2 *pi; %用控制器零点补偿LC滤波器的双极点
wz2 = flc * 2 *pi *kfz; %用控制器零点补偿LC滤波器的双极点
wp0 = fp0 * 2 *pi; %零点处极点频率,决定系统低频增益
wp1 = fesr * 2 *pi; %用来抵消输出电容esr零点的高频极点
wp2 = fesr * 2 *pi *kfp; %低频极点,决定相位提升
%下面是传递函数
% Gs(s) = ((-wp0 * wp1 * wp2)* (s + wz1) * (s + wz2) ) / (s * wz1 * wz2 *(s + wp1)* (s + wp2))
%写入matlab格式的传递函数
fbnum = -wp0 * wp1 * wp2 * conv( [1 wz1], [1 wz2] );
fbden = conv( [wz1 * wz2 0], conv( [1 wp1], [1 wp2] ));
tf_s = tf(fbnum, fbden);
zpk(tf_s);
TF_s = (tf_s)
%连续转到离散系统
Ts = 10e-6; %采样周期10us
TF_d = c2d(tf_s, Ts, 'tustin') %双线性Z变换
[num, den] = tfdata(TF_d,'v') % 提取差分方程系数
[z,p,k] = tf2zp(num,den);
matlab 输出补偿器的s域和z域的传递函数:
TF_s =
-2.133e15 s^2 - 6.379e19 s - 4.766e23
----------------------------------------
2.234e08 s^3 + 2.733e14 s^2 + 3.793e19 s
Continuous-time transfer function.
TF_d =
-4.854 z^3 + 3.504 z^2 + 4.76 z - 3.598
---------------------------------------
z^3 - 0.4289 z^2 - 0.6479 z + 0.07684
Sample time: 1e-05 seconds
Discrete-time transfer function.
num =
-4.8543 3.5038 4.7604 -3.5976
den =
1.0000 -0.4289 -0.6479 0.0768
Matlab 绘出bode:
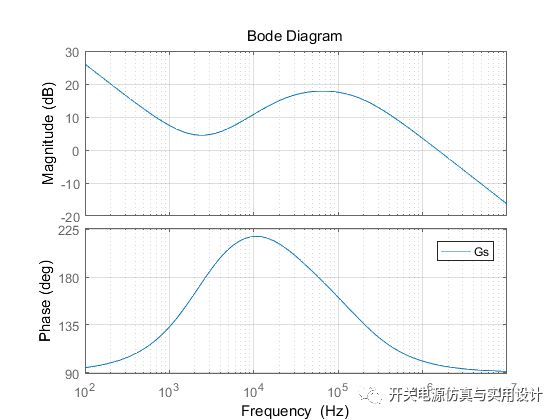
根据z域传递函数编写3P3Z的程序:
/*
* 3p3z_test
*By:maileyang
*Date:2018/03/22
*/
#include <Stdlib.h>
#include <String.h>
#include <math.h>
int g_nInputNodes=0;
int g_nOutputNodes=0;
int g_nStepCount=0;
/*
*3P3Z define
*/
double V_out_sen = 0;
double ctrl_3p3z = 0;
double ctrl_3p3z_1 = 0;
double ctrl_3p3z_2 = 0;
double ctrl_3p3z_3 = 0;
double V_ref = 0;
double error_0 = 0;
double error_1 = 0;
double error_2 = 0;
double error_3 = 0;
double a1 = -0.4289;
double a2 = -0.6479;
double a3 = 0.0768;
double b0 = -4.8543;
double b1 = 3.5038;
double b2 = 4.7604;
double b3 = -3.5976;
double out_max = 9.5;
double out_min = 0.05;
{
V_out_sen = in[0];
V_ref = in[1];
error_0 = V_ref - V_out_sen;
ctrl_3p3z = ( b0*error_0 + b1*error_1 + b2*error_2 + b3*error_3 - a1*ctrl_3p3z_1 - a2*ctrl_3p3z_2 - a3*ctrl_3p3z_3 );
if(ctrl_3p3z <= out_min)
{
ctrl_3p3z = out_min;
}
if(ctrl_3p3z >= out_max)
{
ctrl_3p3z = out_max;
}
out[0] = ctrl_3p3z;
ctrl_3p3z_1 = ctrl_3p3z;
ctrl_3p3z_2 = ctrl_3p3z_1;
ctrl_3p3z_3 = ctrl_3p3z_2;
error_1 = error_0;
error_2 = error_1;
error_3 = error_2;
}
最后在PSIM里面仿真验证3P3Z程序和参数的性能,看看是否达能到设计目的。如果不行,可以在matlab中调整零极点位置,然后离散成Z域传递函数,提取差分方程所需的系数,再次进行仿真即可。
PSIM仿真原理图:
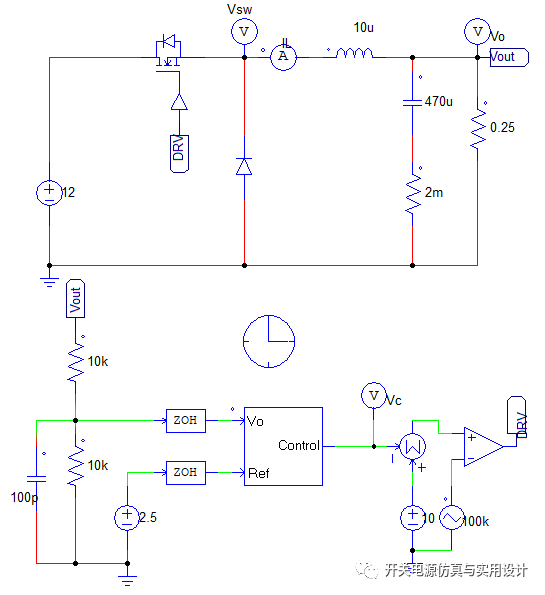
时域仿真:
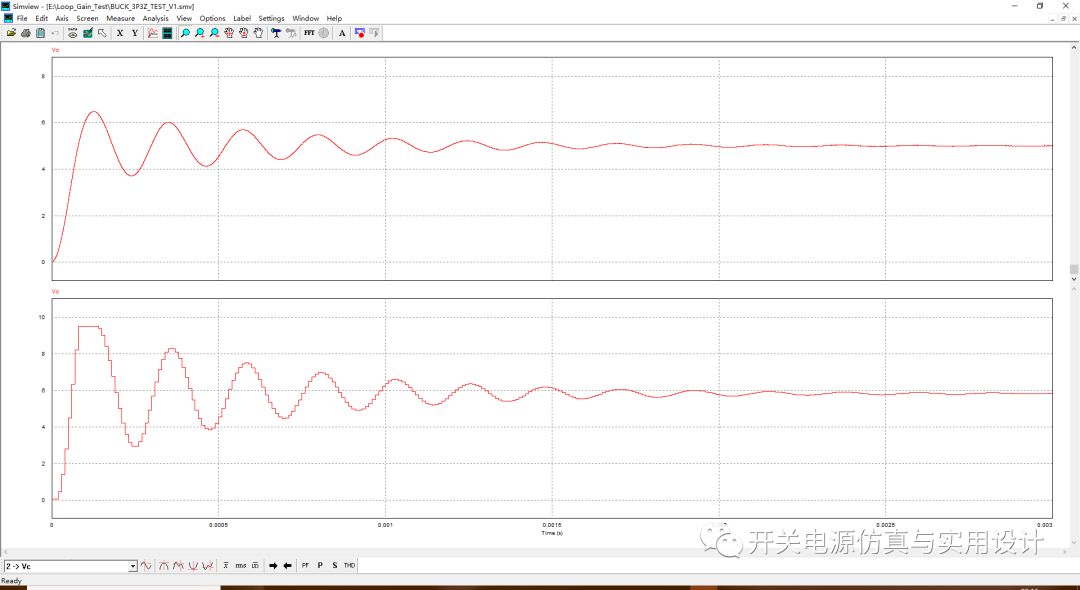
可见这组3P3Z的差分方程的参数还有相当大的优化空间,这就留给亲爱的读者朋友们自行玩耍吧。


 0
0









