Buck电路的工作模式，常见的工作模式是有四种：CCM、BCM、DCM、FCCM(强制连续导通模式)。

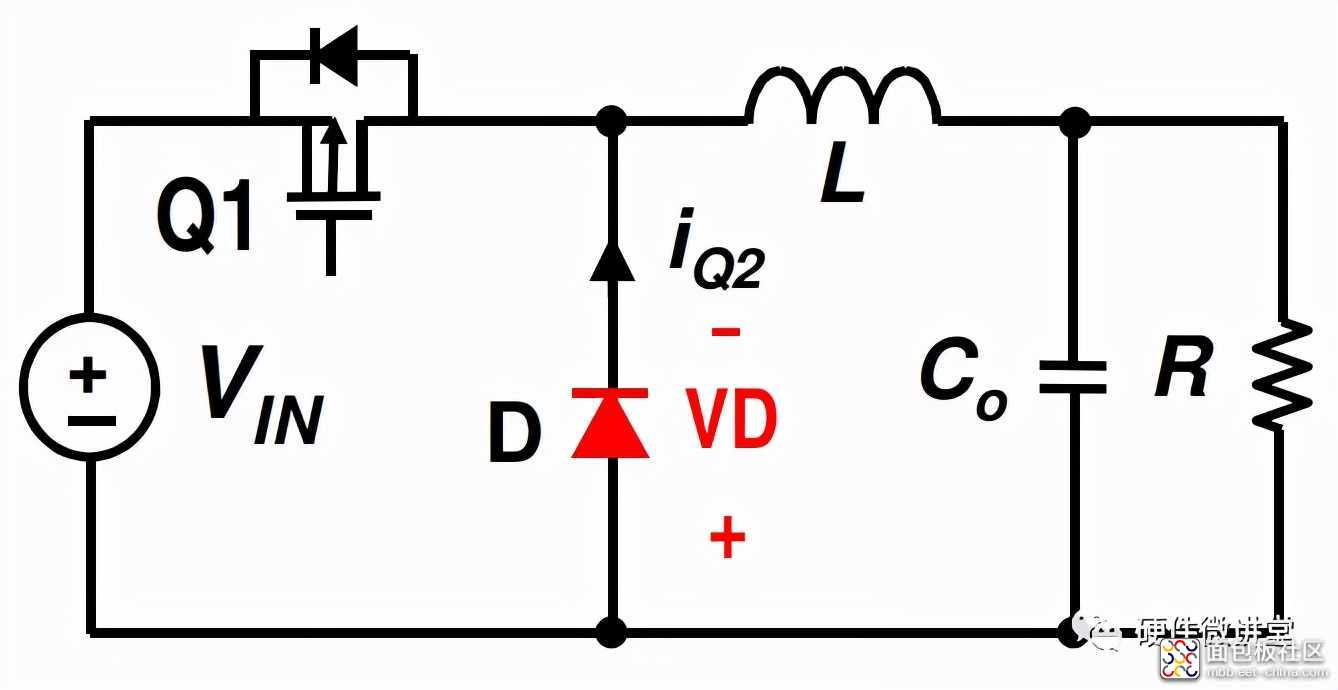
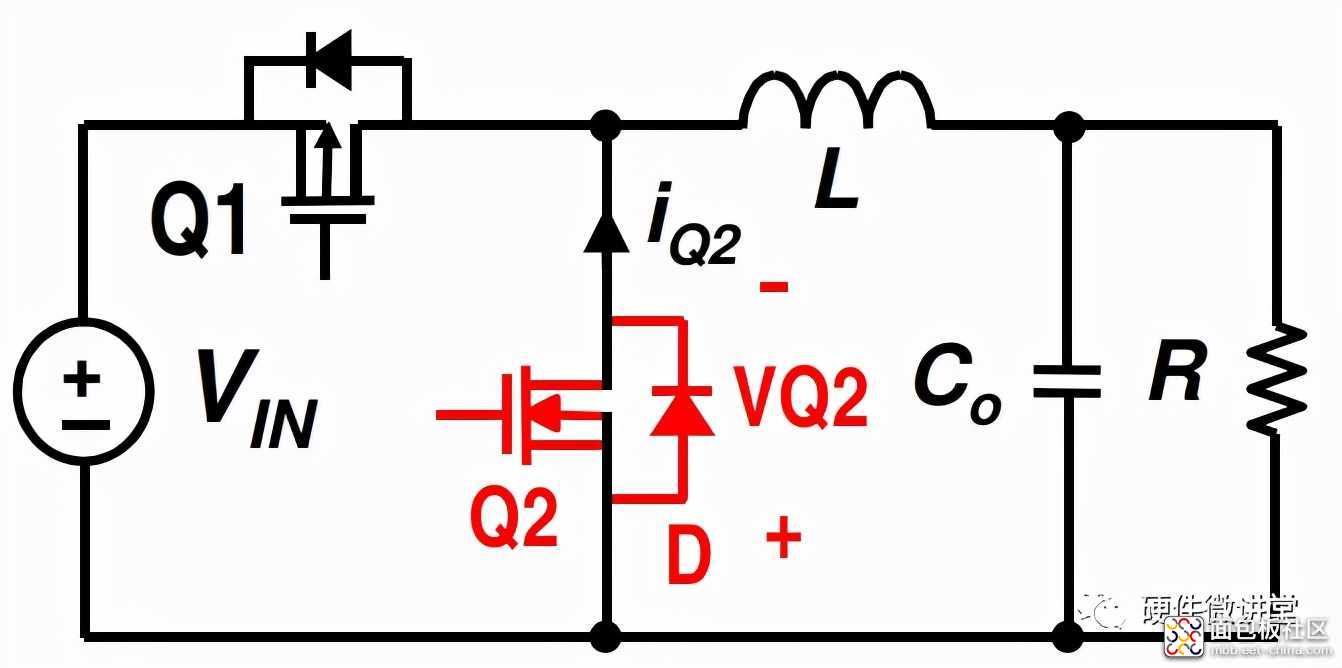
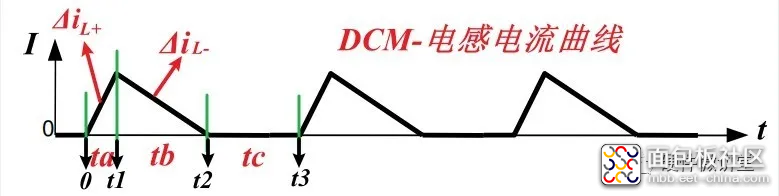
上面提到了4种工作模式，这里重点解析下CCM、BCM和DCM。FCCM后面再做专题解析。下图，3条曲线依次是上述3种模式的电感电流曲线。

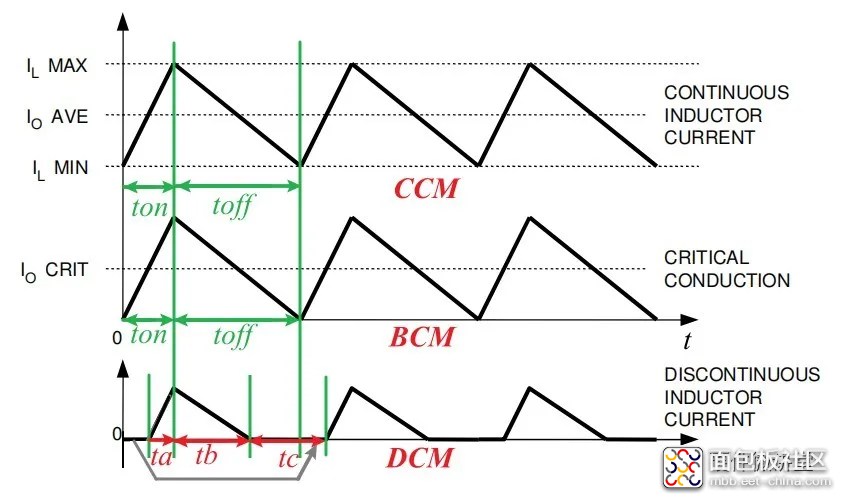
前两条曲线，我们可以看到清晰的ton和toff，这里ton+toff=T。对应异步Buck电路，ton是上管Q1导通，D反向截止的时间。toff是上管Q1关断，D正向导通的时间。

第3条曲线，我们看到有ta，tb和tc。ta对应前面的ton；tb对应前面的toff；tc为系统闲置时间，是L储存的能量释放完，回路中电流已降为零，上管Q1仍然关断，D也关断，而一个开关周期T仍未结束，新的开关周期尚未开始。此时ta+tb≠T，ta+tb+tc=T。由此，也说明了在DCM下toff≠(1-D)*T。

观察上图，我们可以发现：

这里，我们可以得出结论：通过电感电流归零的状态，来辨别Buck电路的工作状态。如果仅仅是回答本小节的问题，看到这里就可以了。但是想要深入了解DCM模式，我们有必要再往下深挖。

Buck电路在稳态时，开关管在导通时电感电流的增量ΔiL+等于在开关管截止期间电感电流的减量ΔiL-。

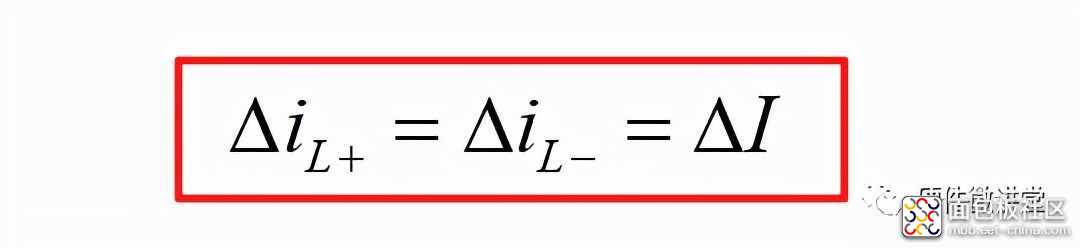
为方便计算，我们将ton对应的ta时间起点定义为0，ta结束时间节点标记为t1，toff对应的tb结束时间节点标记为t2，系统闲置tc结束时间节点标记为t3。

因此，电感电流在0-t1时间段内的增量ΔiL+有如下推导过程：

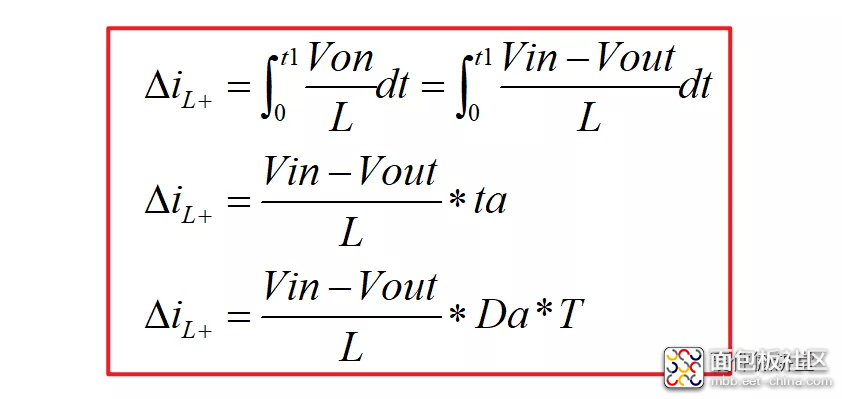
电感电流在t1-t2时间段内的减量ΔiL-有如下推导过程：

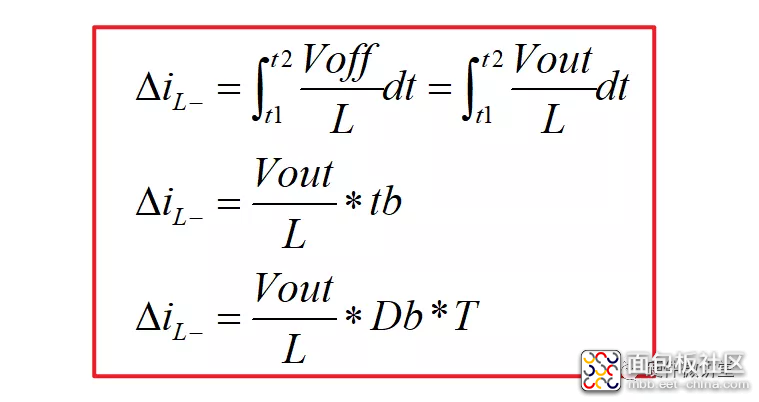
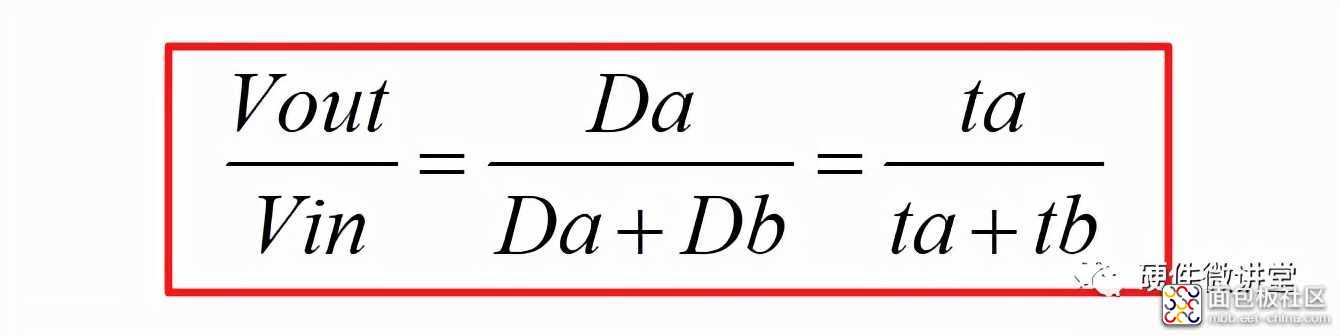
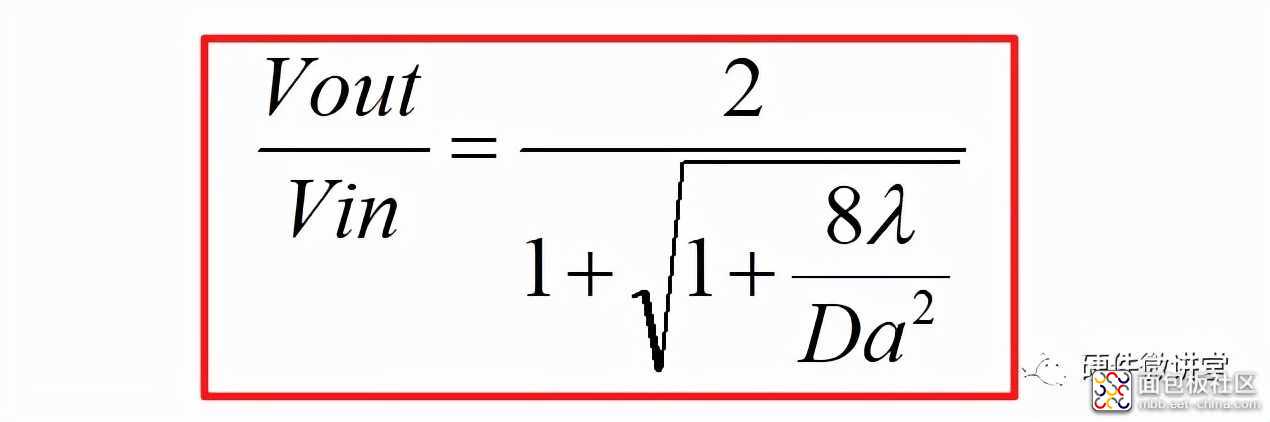
其中，λ=L/RT。由此可以看出，该传递函数要比CCM的Vout/Vin=D要复杂很多。由此，我们又可以得出一个结论：在理想条件下，CCM的输出电压Vout只与占空比有关系，与负载、电感等无关。而DCM的输出电压Vout与电感L、负载电阻R、导通占空比Da、开关周期T都有关系。

不管是从CCM转到DCM，还是从DCM转到CCM，都需要经历BCM。BCM就是CCM和DCM之间的临界状态。掌握了BCM的临界状态，就能控制CCM与DCM之间的转化关系。

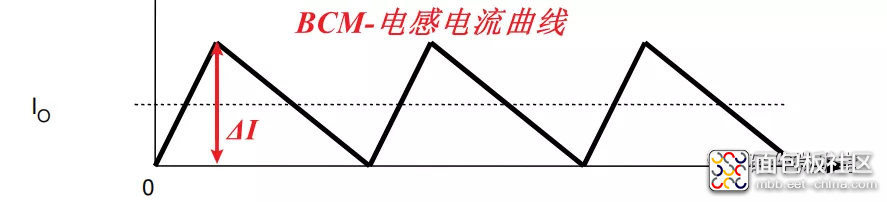
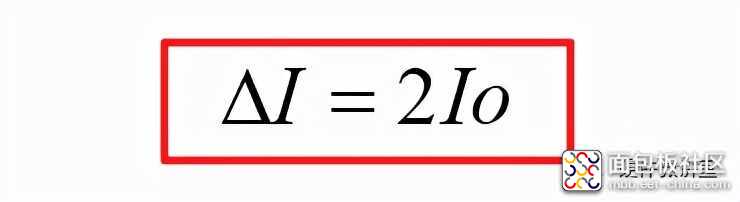
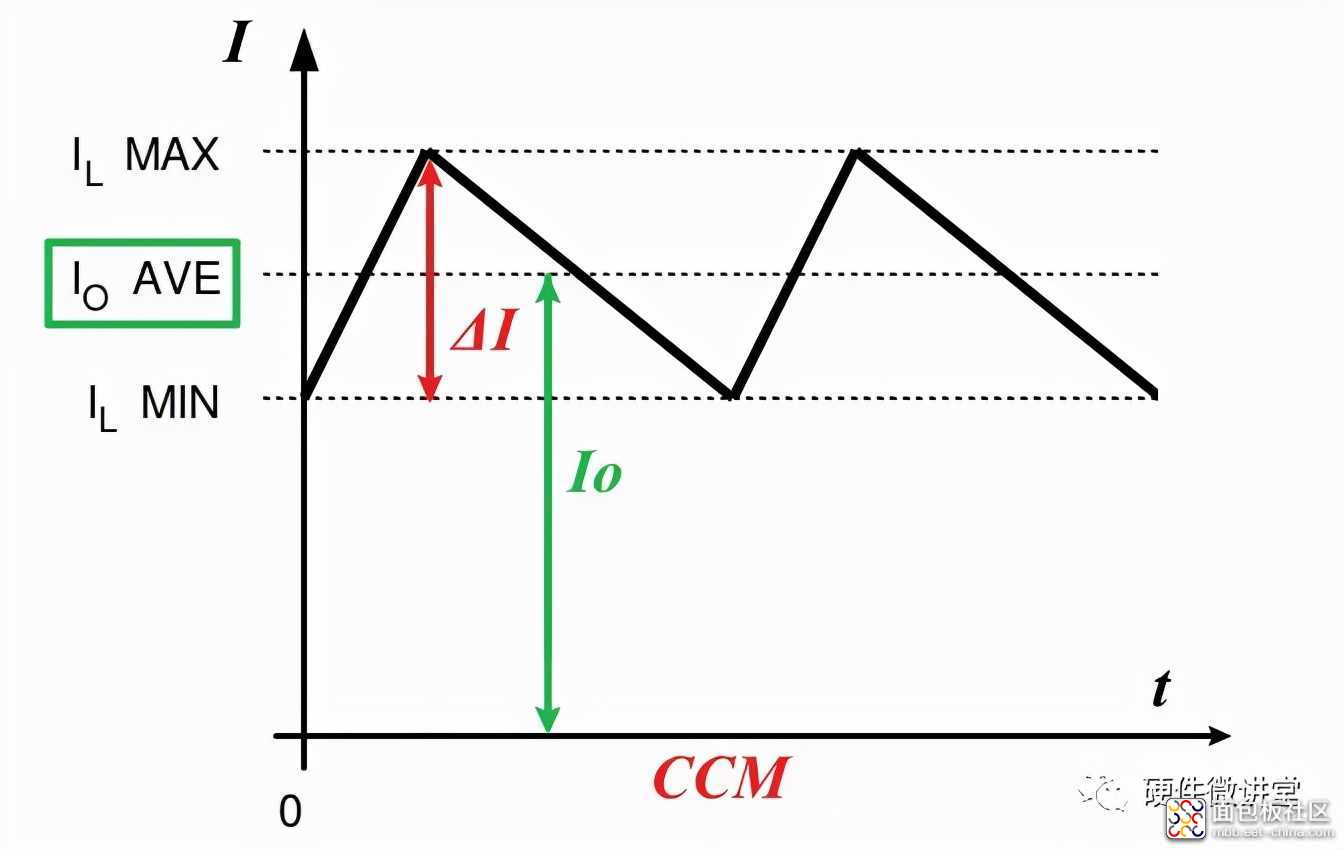
如果想让Buck电路从CCM模式转到DCM模式，就是要降低输出电流(负载电流)Io或者增大ΔI，可用方法如下：