振荡电路物理模型
一个具有正反馈的系统(如图),只要满足以下两个条件就可能产生振荡:
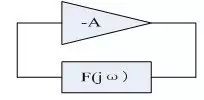
幅度条件:
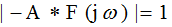
相位条件:
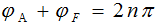
任何一种振荡系统都有两个基本特性:一个是连续振荡特性,用角频率ω表征;另一个是能量衰减特性,用衰减系数Г表征。
振荡信号的数学模型:
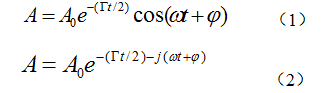
A:振荡幅度,e-jωt:振荡特性,e-Гt/2:衰减特性,φ:初始相位。
由于振荡系统的能量正比于幅度平方(E~|A|2)则有:E = E0e-Гt。因此,单位时间内的能量衰减为:(-dE/dt) = E0Гe-Гt = EГ ,而每周期内系统损耗的能量表示为:EГ/f。那么,系统总能量E与EГ/f之比为:fE/EГ = f/Г = ω/2πГ。这个比值反映了振荡的持续能力,也就是Q值。即2πQ = ω/Г,振荡系统Q值越高,其维持振荡的能力越强谱线越窄,通常衰减系数Г就是谱线半功率点的宽度。
为什么石英晶体振荡器具有很高的频率稳定度呢?这是由于石英材料所具有压电效应使之具有高Q值,在振荡电路系统中,石英谐振器等效为电感L,且感量很大,通常为104~5 这就使系统Q值很高,维持振荡的能力很强,其谱线半功率点宽度(BW)很窄,所以振荡系统的频率很稳定。







 /5
/5 

