本文将从状态估计讲起,按照SLAM的滤波器原理发展历程依次对卡尔曼滤波、拓展卡尔曼滤波、粒子滤波以及Fast SLAM讲述SLAM的算法演变。
状态估计
要讲SLAM方面的贝叶斯的滤波器实现方式,那么就要从状态估计问题开始讲起了。其实SLAM系统所用到的传感器,激光也好,视觉也好,整个SLAM系统也好,要解决的问题只有一个:如何通过数据来估计自身状态。每种传感器的测量模型不一样,它们的精度也不一样。换句话说,状态估计问题,也就是“如何最好地使用传感器数据”。可以说,SLAM是状态估计的一个特例。

卡尔曼滤波器
在状态估计问题中,最简单的系统是线性高斯系统。而卡尔曼滤波器针对的就是这种最简单的系统,卡尔曼滤波是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
在此系统中,运动方程、观测方程是线性的,且两个噪声项服从零均值的高斯分布。线性系统可以用方程直接表示出来:
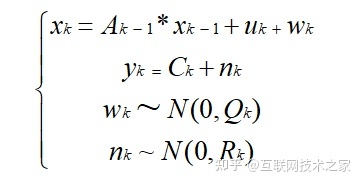

扩展卡尔曼滤波器
卡尔曼滤波器理论当然是一个比较成熟的SLAM领域的经典理论,但是在现实生活中,很多的系统都不是线性的,状态和噪声也不是高斯分布的,比如激光的观测方程线性的。当一个系统为非线性时,那么高斯分布经过该系统后将不再是高斯分布的,如果没有高斯分布的前提,那么我们在进行状态求解的过程中那些高斯领域的经典求解方法也将无效。
鉴于此,在卡尔曼滤波器这种只能运用在线性高斯(LG)系统的滤波器的前提下发展出来了扩展卡尔曼滤波器EKF的基本思想是将非线性系统变换为线性系统,然后进行卡尔曼滤波,因此它是一种次优滤波器。
EKF的做法主要有两点:
其一,在工作点附近和来对系统进行线性近似化:
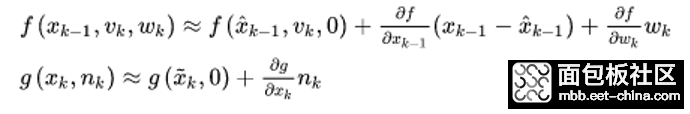
这里的几个偏导数,都在工作点处取值。于是呢,它就近似化当成了一个线性系统。
其二,在线性系统近似下,把噪声项和状态都当成了高斯分布。这样,只要估计它们的均值和协方差矩阵,就可以描述状态了。经过这样的近似之后,后续工作都和卡尔曼滤波是一样的了。所以EKF是卡尔曼滤波在非线性非高斯系统下的直接扩展。EKF给出的公式和卡尔曼是一致的,用线性化之后的矩阵去代替卡尔曼滤波器里的转移矩阵和观测矩阵即可。
粒子滤波
粒子滤波算法的核心思想是利用一系列随机样本的加权和近似后验概率密度函数,通过求和来近似积分操作。该算法源于Monte Carlo思想,即以某事件出现的频率来表示该事件的概率。因此在滤波过程中,需要用到概率的地方,都对变量采样,以大量采样及其相应的权值来近似表示概率密度函数。这样一来,粒子滤波可以用来近似任意形式的概率,而不仅仅局限于高斯分布。
假设系统状态方程和观测方程如下所示:

FastSLAM
上述的粒子滤波器虽然可以比较有效地克服我们在很多时候不能用具体某个分布来描述我们的状态或者观测输出的问题,而是通过采样的方式来确定我们所要研究的分布问题。但是这个这种采样思路的最大问题是:采样所需的粒子数量,会随分布呈现指数增长。对高维空间进行采样,随着机器人的不断探索,环境特征数会不断增加,这样一来样本数目会随之而呈指数增长,这样下去粒子滤波算法的效率会越来越低。
鉴于此,FastSLAM算法应运而生,传统的SLAM 问题的解决方法都是针对机器人位姿以及地图的后验概率进行估算求解,但是Fast SLAM算法的精妙之处就是其针对机器人的路径和地图进行求解。






 /5
/5 

