电抗元件如何影响 LC 电路中的相移？详细了解模拟设计中的相移。

本文将讨论相移，即电路导致电压或电流从其输入到输出的超前或滞后的影响。特别是，我们将关注无功负载和网络如何影响电路的相移。

我们将专门研究相移如何影响完全可靠的运算放大器，以及如何在某些谐振网络拓扑中使用电抗元件来发挥我们的优势。

在上一篇文章中，我们了解了如何对电路中电抗元件引起的相移进行建模。现在，让我们将到目前为止学到的知识应用到运算放大器电路中。

下面是一个用作简单缓冲器的运算放大器。

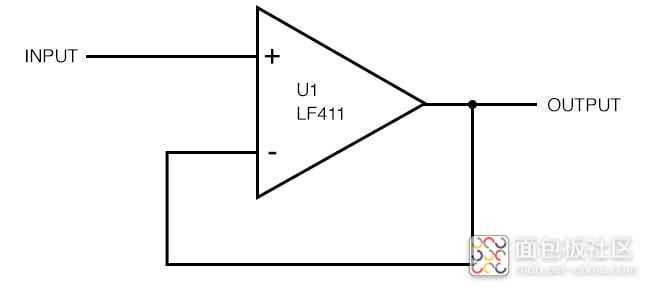
在相位开始下降之前，响应均匀且平坦高达 1 MHz。

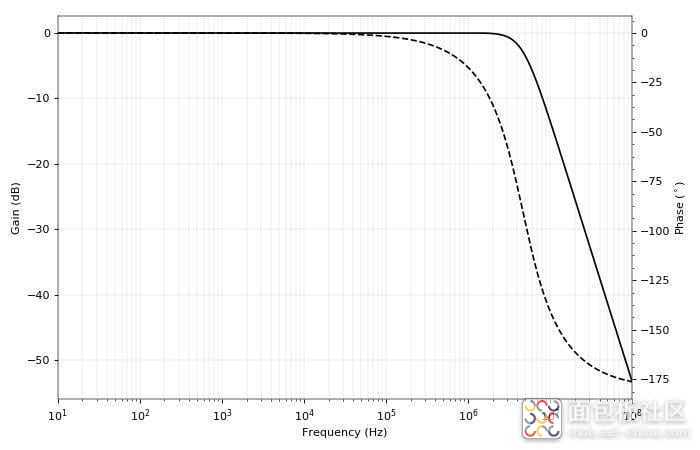
该电路依赖于负反馈（同相输出到反相输入），-180° 相移导致负反馈变成正反馈（180° 相移输出到反相输入）。

现在让我们尝试用电容器加载电路。

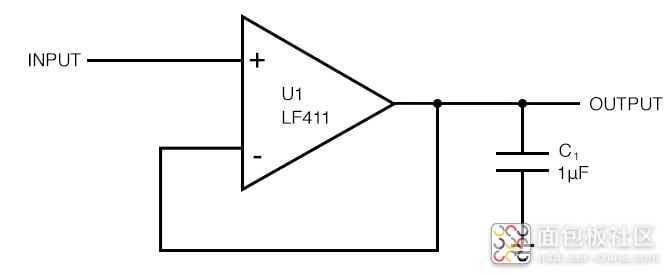
如果运算放大器具有阻性输出阻抗，对于此运算放大器（LF411），单位增益约为 0.1 - 10 Ω，我们预计该电容器会导致高于截止频率的 -90° 相移。让我们看看发生了什么。

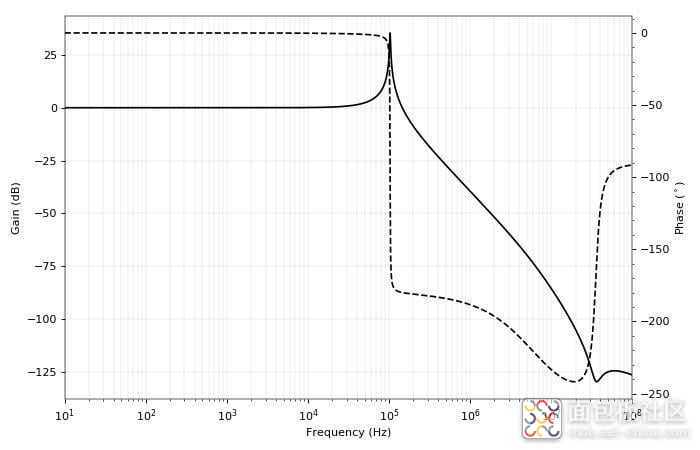
那看起来很糟糕。振幅响应有一个共振峰值，相位突然下降到 -180°，这是振荡的完美配方。必须至少有三个电容（电感不太可能）导致这些响应变化。有了我们的嫌疑人，我们就可以遍历电路并找出到底是什么导致了问题。

相移在反馈网络、谐振网络和振荡器等电路中变得尤为重要。我们可能希望在我们的电路中有一个 90° 的相移以有意地控制相位。很简单，我们可以添加一个电容器（或者对于冒险者来说，一个电感器）来分流输出，看看它能把我们带到哪里。

事实上，我们可能不希望负载上只有90° 相移。也许我们想要 180°。

也许我们会再放第二个电容器？

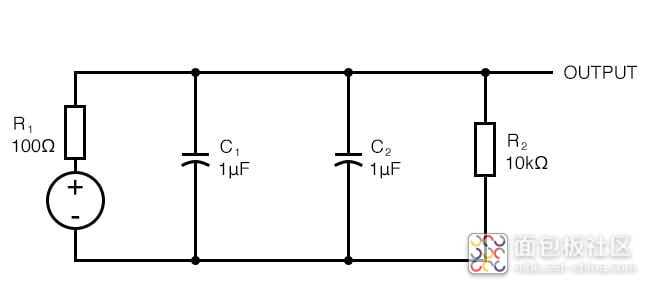
那是行不通的——两个并联电容器只是形成一个等效电容器。它们都共享相同的电压，因此它们不能同时贡献不同的滞后量。我们需要更有创意。

实现这种效果的一种方法是使用多级 RC 滤波器。但更可取的途径可能是将电容器与一个或多个电抗元件分开，如以下电路所示。

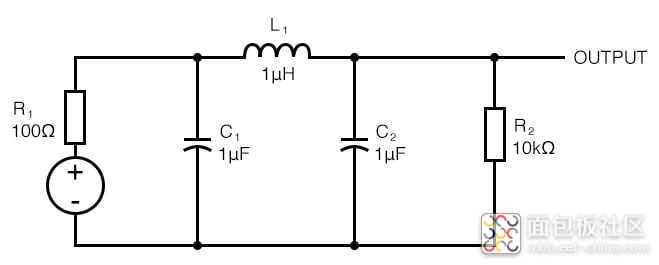
该电路是一个低通滤波器，它将以与由 1 μF 电容器和 0.5 μH 电感器（或 0.5 μF 电容器和 1 μH 电感器）组成的谐振网络相同的频率谐振。

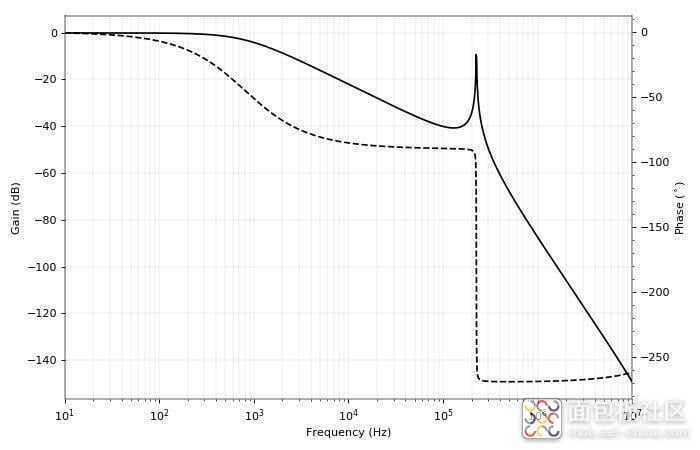
从响应和相移我们可以看出，电路的行为类似于 RC 滤波器，源电阻器和两个电容器并联，在谐振峰值前不久达到 -90°。然后出现谐振峰，相位骤降至 -270°（三个电抗元件的相移）。恰好在谐振时，相移是所需的 180°。

该电路用作 Colpitts 振荡器中的谐振元件，电感器-电容器-电感器变体用于 Hartley 振荡器。通常，电路会绘制成图 8 所示的样子。

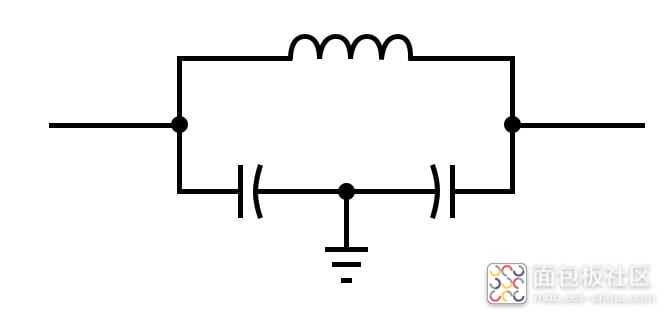
虽然它可能会稍微混淆元件的用途，但如图 8 中所示绘制元件给出了单个谐振元件的外观。您可以在图 9 中看到一个带有以这种方式绘制的谐振网络的 Colpitts 振荡器示例。

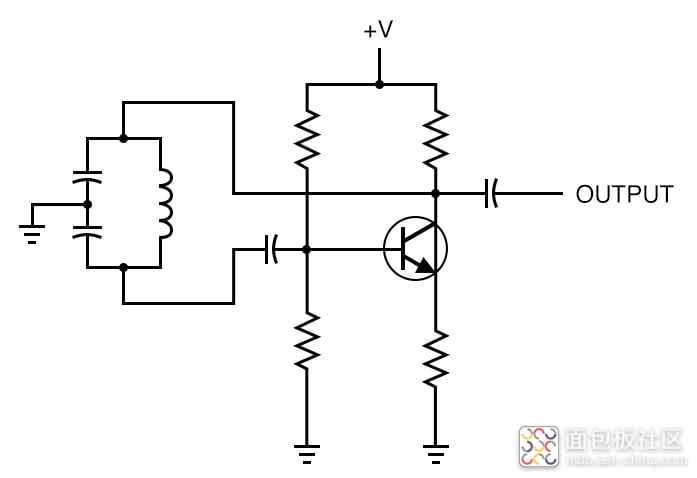
两个例子引起了一些共鸣。因为谐振元件依赖于电抗元件提供相移的能力，所以多谈谈谐振电路中的相位将是说明性的。

当电感器的电抗与电容器的电抗相等时，串联 LC 电路谐振。此时，电感和电容共享相同的电流；理想情况下，电感器提供 +90°（超前）电压相移，而电容器提供理想的 -90°（滞后）电压相移，这意味着电路末端的电压为 0° 异相（无压降、短路）。类似的效果会产生 LC 谐振回路。

但正如我们现在所知，当源或负载阻抗设置正确时，电容器和电感器只能提供 +/- 90° 相移。以这个谐振回路为例。

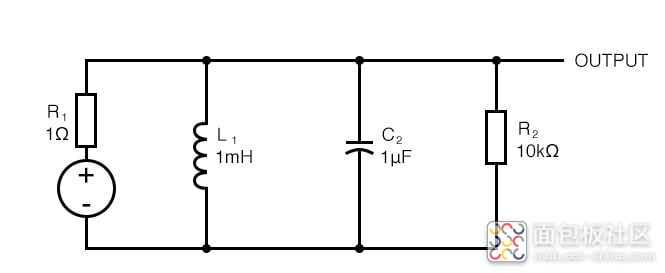
源阻抗仅为 1 Ω，负载为 10 kΩ。坦克应该在 5 kHz 下共振。我们可以通过应用输入阶跃并寻找振铃来测试共振。模拟结果如下。

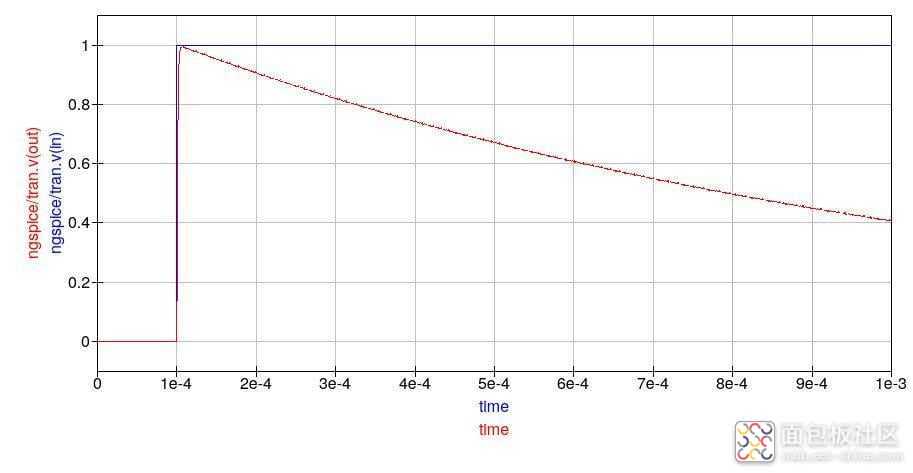
坦克似乎并没有响太多。原因在于源阻抗，鉴于我们的 L 和 C 值，它太低了。我们希望我们的电容器和电感器能够在谐振频率下快速来回交换能量，但效果会减弱，因为谐振回路 Q 因数太低。

有几种方法可以理解这一点。在相移的背景下，我们可能会提出以下解释。单独查看源阻抗和电容器，我们发现它们形成了一个截止频率为 160 kHz 的低通 RC 滤波器。相反，源阻抗和电感器构成一个截止频率为 160 Hz 的 RL 高通滤波器。

如果我们同意谐振回路的行为取决于组件提供的相移（来自电容器的 -90° 电压相移，来自电感器的 +90° 电压相移），那么阻尼的原因就很明显了。

RC 低通滤波器将提供高于其截止频率的 -90° 相移，RL 高通滤波器将提供低于其截止频率的 +90° 相移。回路的谐振频率 5 kHz 对于 RL 滤波器而言太高而无法提供正相移，对于 RC 滤波器而言太低而无法提供负相移。

以这种方式推理，我们通过改变 L 和 C 的值（同等地降低电感和增加电容）或改变源阻抗来诱使电路产生振铃。

增加源阻抗具有预期的效果。

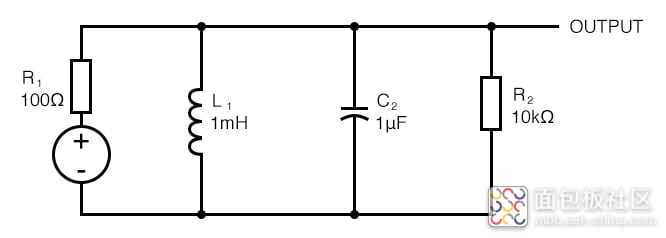
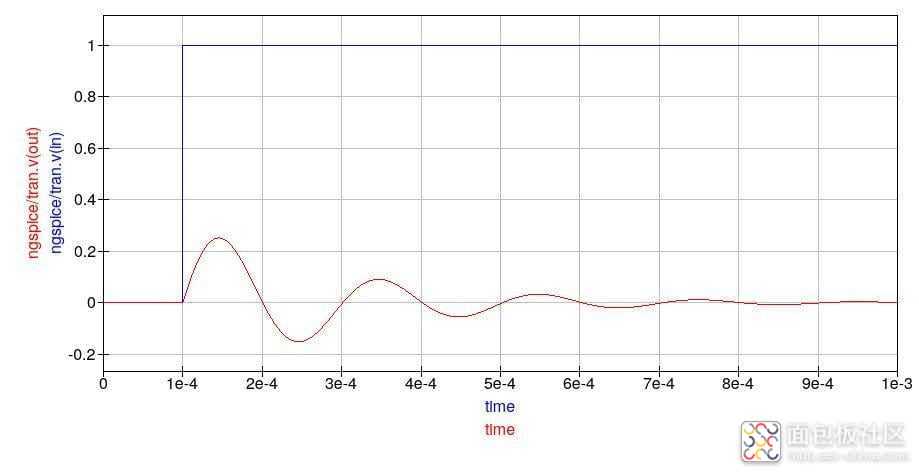
现在，正如预期的那样，槽路振铃，周期为 0.2 毫秒（对应于 5 kHz 的谐振频率）。

本文仔细研究了模拟电路中的相移。我们的主题让我们了解了各种电路：放大器、滤波器、谐振回路和振荡器。电容器和电感器总是会引起相移，但效果受源阻抗和负载阻抗的影响。在这里，我们主要假设源阻抗和负载阻抗是电阻性的。然而，反应性元素总是存在的。

要分析电路中的电抗元件，我们应该考虑为元件供电的电路的输出阻抗，以及后续电路的输入阻抗。现在，当我们希望电路以特定方式运行时，我们可以使用我们对相移的直觉来指导我们，将我们推向正确的方向。