前面介绍的傅里叶变换是在频域内分析波的特性,但对于无限放大的信号,却无法处理,所以必须对范围推广到复频域,如果把傅里叶变换看做是二维空间的话,那么拉普拉斯变换就是三维空间。
学过信号处理和高数的伙伴对这个公式并不陌生,看上去很乏味,其实背后的原理让人着迷:

因为是推广到复平面,首先我们来看含有复数的指数参数含义:
如下s是个复数,所以可以分解为实部和虚部,但对时间而言S始终是常量,
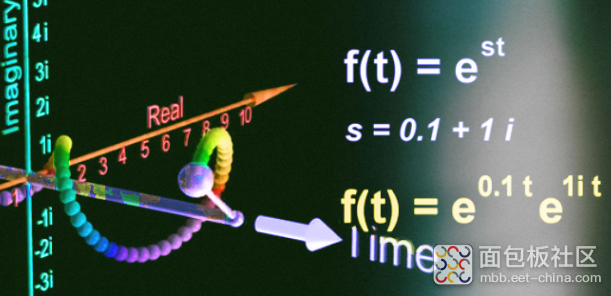
但对整体e^s而言,它的旋转半径是e^0.1t, 旋转角度是1t ,所以图像是半径不断增加的螺旋状。
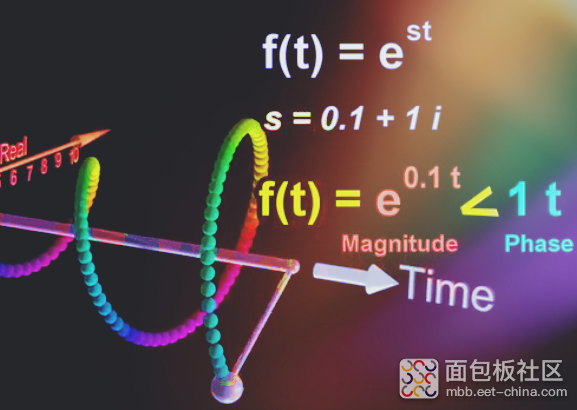
如果增加s虚部:
意味着同一时刻的旋转角度增加,即杆子的速度加快
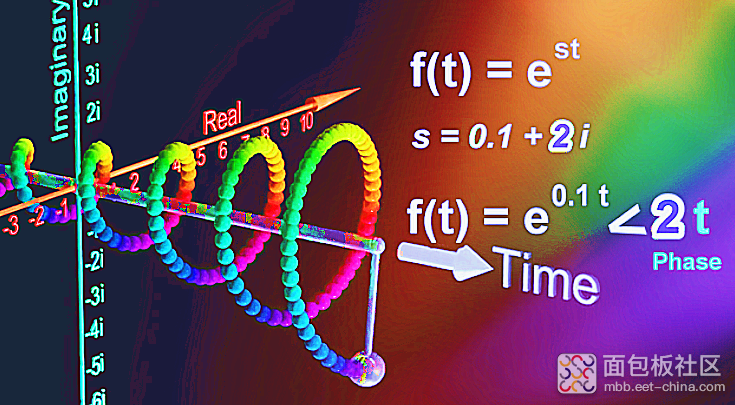
比较:2t相比上面的1t而言,同一时刻的旋转角度增加,会旋转的更快,螺距会变小
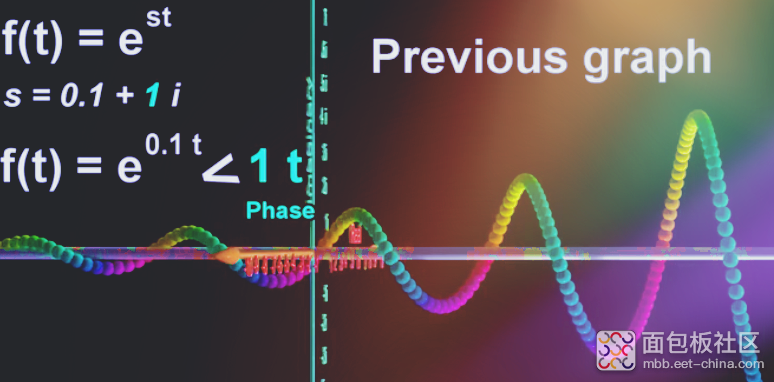
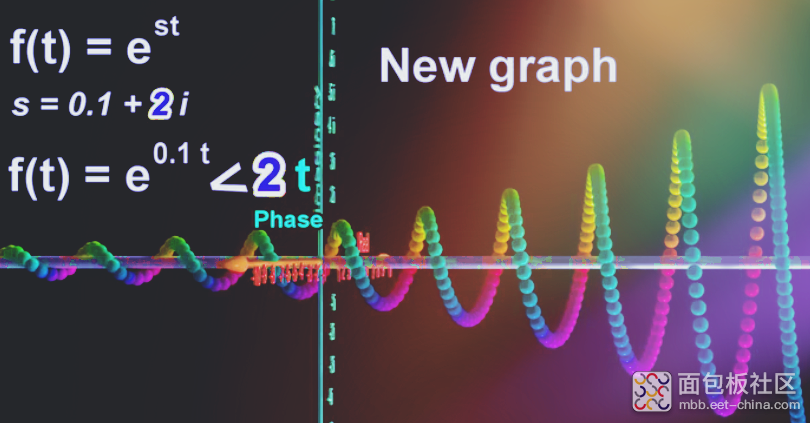
如果增加s的实部
意味着旋转半径会变大,如下e^0.2t时图形
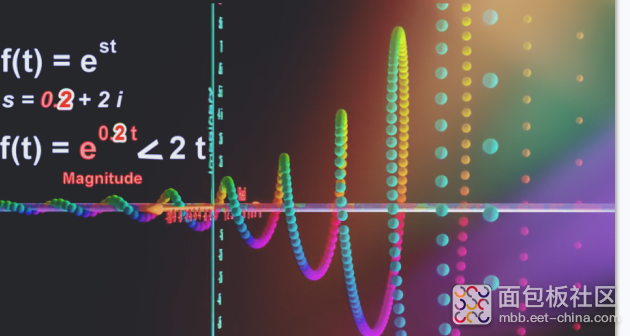
e^0.1t时图形
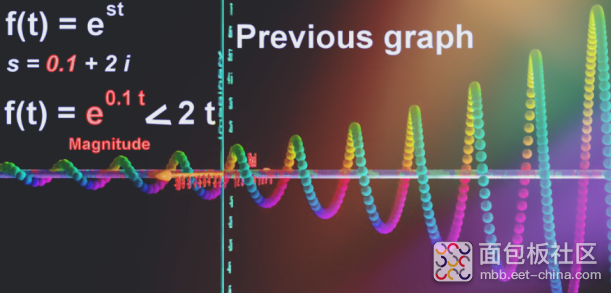
但同一时刻的旋转角度不变,所以螺距不变,仅是旋转半径增大。
如果实部为零,则旋转半径是常数1,图形就是一个均匀的螺旋线。其实这就是傅里叶变换的特性
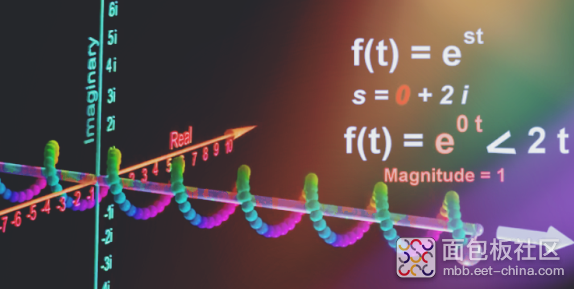
实部是3时,就是一个旋转半径为3的均匀螺旋线。
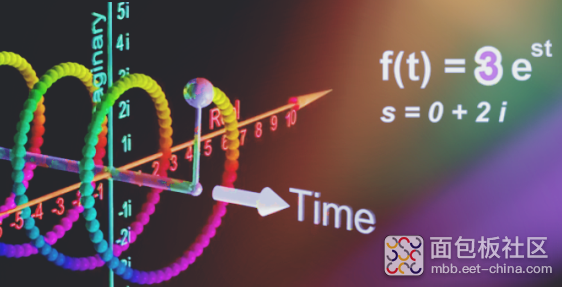
如图两个实部相等的函数叠加,空间图形就是余弦波,因为他们两个起始角度相反,在空间上抵消,所以仅留下平面上的图形,
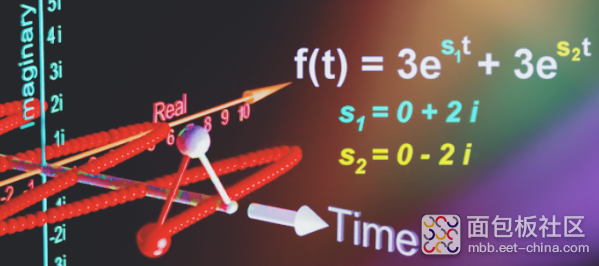
如果改变实部和虚部,将两个指数函数叠加:结合上述的分析和傅里叶级数就很容易理解:
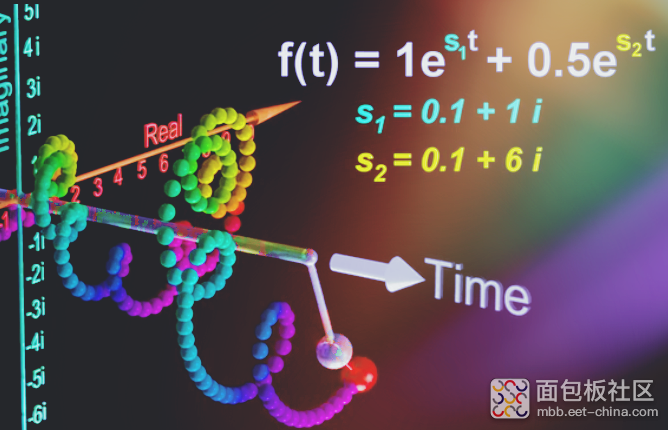
多个指数函数叠加,因为起始角度相互抵消,所以就留下水平面上旋转半径不同的图形。
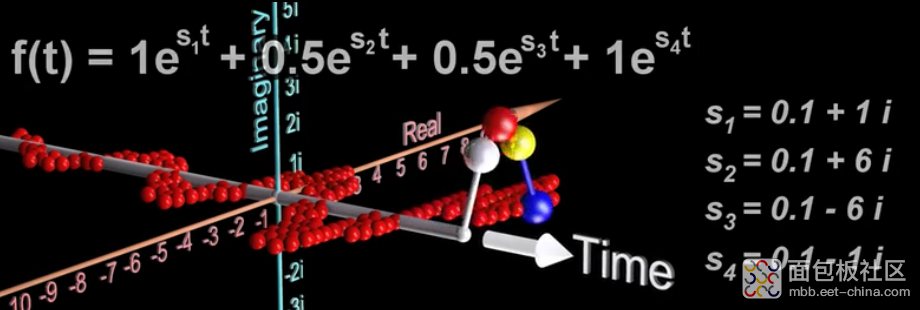
如图

通过这种方式将指数函数叠加在一起就可以创建任意的图形,这是本篇的重要思想。
结合前面的傅立叶级数和傅里叶变换,我们可以看到复指数将波形拓展到空间的任意角落,这是傅立叶变换所没有的,下一篇继续讨论由此得出的拉普拉斯变换公式原理。







 /2
/2 

