非线性负载不断变化的阻抗会导致电流成非正弦表现;因此,该等负载会导致谐波电流,其频率是基本频率的整数倍(基本频率为50或60 Hz,视地区而定)。当这些谐波电流在系统阻抗中传播时,供电电压上就会出现被称为谐波电压的失真现象(正如您可能猜到的,谐波电压是频率为基本频率整数倍的电压)。
这些电流和电压谐波会损坏其他接入电网的电气设备,包括公用设施和其他电气用户的设备。因此,电力供应商和能源使用大户有责任降低非线性负载及其相关谐波的影响。第一步便是监控电网中是否存在谐波。在电表中加入总谐波失真率(THD)测量是个不错的开始。
在探讨如何计算THD这样的细节问题之前,首先让我们来了解下谐波的基本概念。关于谐波首先应该注意的是您可以将谐波导致的波形分解成正弦波的叠加。在对得到的波形进行分解的过程中,额定频率的分量称为基本频率。频率为基本频率整数倍的正弦波分量称为谐波,n次谐波对应基本频率n倍的频率分量。在图1中,您可以看到3次谐波电压分量和基本电压是如何共同创造出由正弦波衍生出的新波形的。
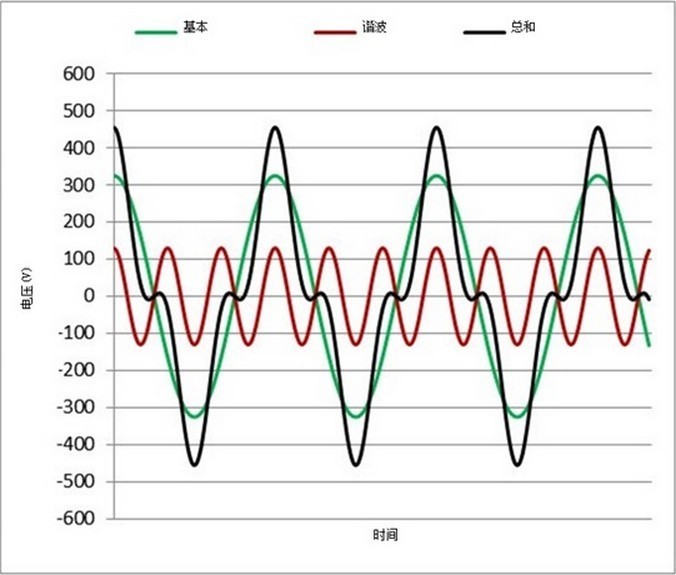
图1:带3次谐波电压分量的电压波形范例
电压和电流中出现谐波时,您可以使用所得波形(例如,图1中的黑色波形)的波形样本进行相应的均方根(RMS)测量并将其插入标准均方根方程,方程1和方程2中:

如果您已知每个谐波分量的均方根值和基波分量的均方根值,那么,您可以通过每个谐波分量及基波分量总均方值的平方根,交替计算出RMS,如方程3和方程4所示:
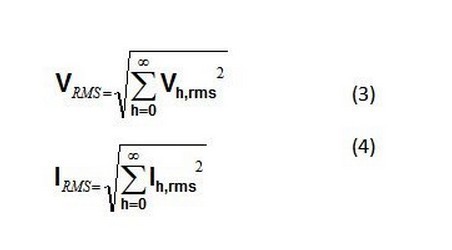
您可以按照信号中全部谐波含量计算THD参数。对于THD,有两个常用的定义。第一个定义来自IEC 61000-4-7,其将THD定义为指定次(N)全部谐波分量均方根值(V1,rms表示电压,I1,rms表示电流)与基波分量均方根值(Vh,rms表示电压,Ih,rms表示电流)之比。方程5和方程6分别是计算电压和电流THD的方程:
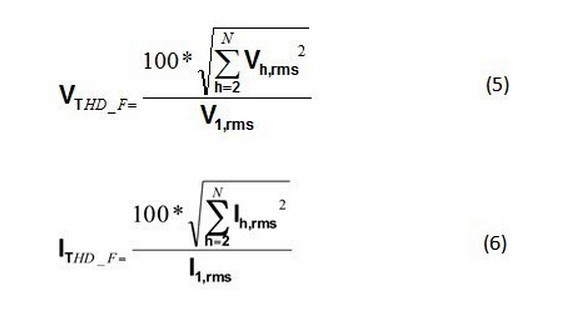
这一THD定义更常见于能源计量系统,如果基本信号的贡献小于其他谐波的总贡献,得到的THD值可能会超过100%。
在对THD的第二个定义中,THD是指定次(N)全部谐波分量均方根值(Vh,rms表示电压,Ih,rms表示电流)与总均方根值(V1,rms表示电压,I1,rms表示电流)之比。总RMS值包括基波和其他谐波的作用。方程7和方程8分别是计算电压和电流THD的方程:

在THD的第二个定义中,由于总均方根被用作分母,而不仅仅是基波均方根值。因此,得到的值总小于100%。
因此,在测试THD精度时,需注意所使用的THD定义,因为这两个不同的定义会得出两个不同的值。
在两个定义中,您都必须确定每个谐波分量的均方根值。计算这类均方根值要求采用快速傅里叶变换(FFT)运算。根据所选择的计量处理器,这可能涉及很密集的计算操作。
原文链接:
https://e2e.ti.com/blogs_/b/smartgrid/archive/2016/08/19/quantifying-harmonic-distortion-options-for-calculating-thd
译文来源:TI社区




 /5
/5 

