宇宙中最强大的计算机实际上是最简单的。
今天的程序员面临着财富的尴尬。软件工具丰富丰富,硬件强大而便宜。衡量软件工具不断增加的复杂性和复杂性的一种简单方法是查看生成“Hello, world!”需要什么。程序。
在 C 和 Unix™ 的早期,它只需要几行源代码。现在,使用 Windows C/C++ 编译器或其他 GUI 编程工具,即使是生成一个简单的“hello world”程序,也涉及数百行应用程序程序员很少看到的支持代码。
编程环境可能很大,因为今天可用的机器随着价格的下降而功率上升。工具越来越容易使用,调试器越来越复杂。现在是成为程序员的好时机,但有时我们会被软件工具和硬件平台的强大和优雅所蒙蔽。
有时值得退后一步,从第一原则的角度看待这个世界。物理学家(至少是优秀的物理学家)从第一原理来看世界。在数学中,第一性原理被称为公理。
摆脱编写程序的日常工作并根据公理来思考计算机是令人耳目一新的。公理与编写计算机程序有什么关系?试着回答这个简单的问题:什么是计算?
什么是计算?
答案是:图灵机中导致停止状态的配置序列称为计算。这意味着如果你的算法在图灵机上成功运行,它就是一个计算。如果不是,那么它不是计算!
答案是:图灵机中导致停止状态的配置序列称为计算。这意味着如果你的算法在图灵机上成功运行,它就是一个计算。如果不是,那么它不是计算!
我们所知道的世界在 1936 年发生了变化。在胡佛水坝开始发电的同一年,雪莉·坦普尔 (Shirley Temple) 成为票房冠军,一位名叫艾伦·图灵 (Alan Turing) 的 24 岁英国人完成了一篇名为“关于可计算数字”的论文应用于Entsheidungsproblem。
Entsheidungsproblem 是可判定性问题的德语表达方式。
什么是可判定性?
可判定性意味着“可以开发一种算法来解决产生是或否答案的特定问题吗?”
可判定性意味着“可以开发一种算法来解决产生是或否答案的特定问题吗?”
为什么对可判定性如此恶臭?从 1910 年开始,一直持续到 1913 年,阿尔弗雷德·诺斯·怀特黑德 (Alfred North Whitehead) 和伯特兰·罗素 (Bertrand Russel) 发表了被认为是开创性数学著作之一的《数学原理》。在这三卷集中,怀特黑德和罗素试图将整个数学简化为形式逻辑的一个子集。他们打算证明数学是完整的。在这种情况下,完整一词的含义意味着可以通过某些机械方式生成证明或公式。根据已知为真的公理,可以将其他细节和条件添加到机械算法中以创建新的证明。这种观点,就像在牛顿物理学中一样,提供了一种类似发条的、确定性的世界观。1931 年,库尔特·哥德尔提出了他的不完备性定理,这有效地表明,我们作为数学真理所持有的基本概念无法被正式证明。这种不完整性甚至适用于简单的数字。这打破了怀特黑德和罗素关于磨出机械证明的概念,进而动摇了数学的基础。如果构建问题的基础不完整,怎么可能有决定性?
在他有点晦涩的论文中,图灵描述了一种抽象的通用计算机,现在称为图灵机。
事实证明,没有比图灵机更强大的机器,无论是理论上的还是现实的。
图灵机是现代计算机科学的基石。正如他从一开始就坚持的那样,图灵的抽象机器实际上是可以建造的。
不幸的是,1936年也是4000名纳粹军队悄悄潜入莱茵兰,占领凡尔赛条约规定的非军事区的一年,预示着二战的开始。
1940 年,英国处于战争状态,德国 U 型潜艇无情地摧毁了护航船,图灵(和其他有才华的数学家)被英国高级指挥部征召,帮助破解德国的军事密码。
幸运的是,从一艘正在下沉的 U 艇中捕获了一台名为“Enigma”的德国秘密密码机。凭借捕获的 Enigma 的额外奖励,图灵破解了所谓的牢不可破的 Enigma 密码,并在盟军赢得北大西洋战争的过程中发挥了重要作用。
战争的不幸影响是它停止了通用图灵机的开发和实现。
二战后,英国和美国之间为了建造第一台数字计算机而进行的一场竞赛已经开始并开始了。英国正在建造 ACE(自动计算引擎),美国正在建造 ENIAC(电子数值积分器和计算器)。图灵处于 ACE 项目的外围,而不是硬件设计的核心,因此他将思想转向了指令表,或者我们现在所说的软件。
标准图灵机
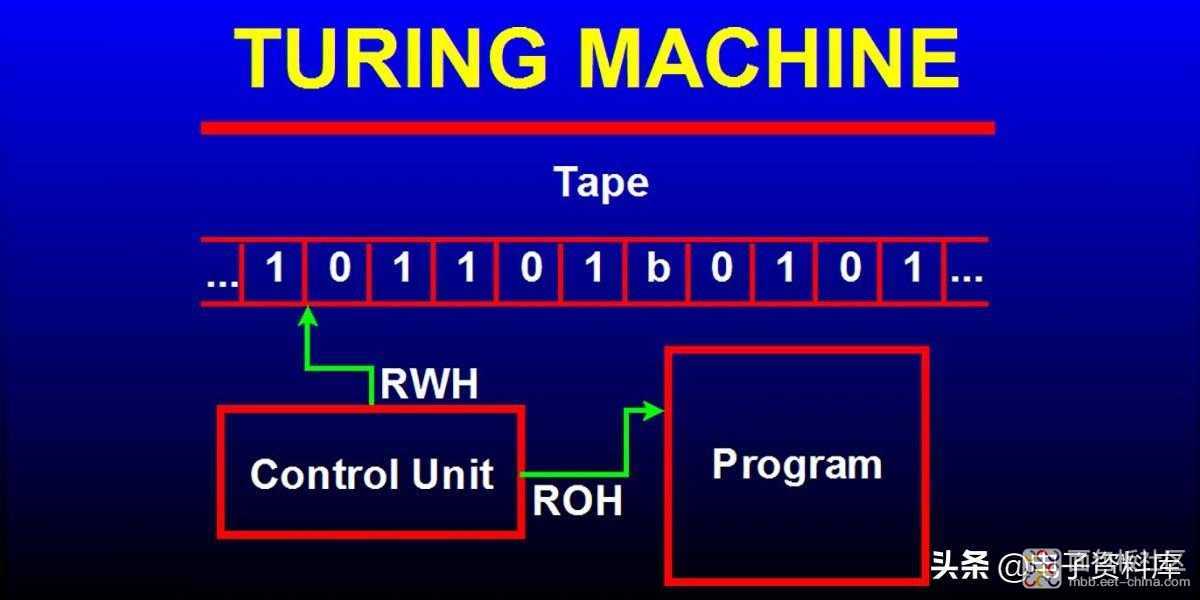
标准图灵机如图 1所示。它由一个读/写磁头和一个无限长的磁带组成,可以一次向右或向左移动一段。读/写头在磁带上读取和写入符号。
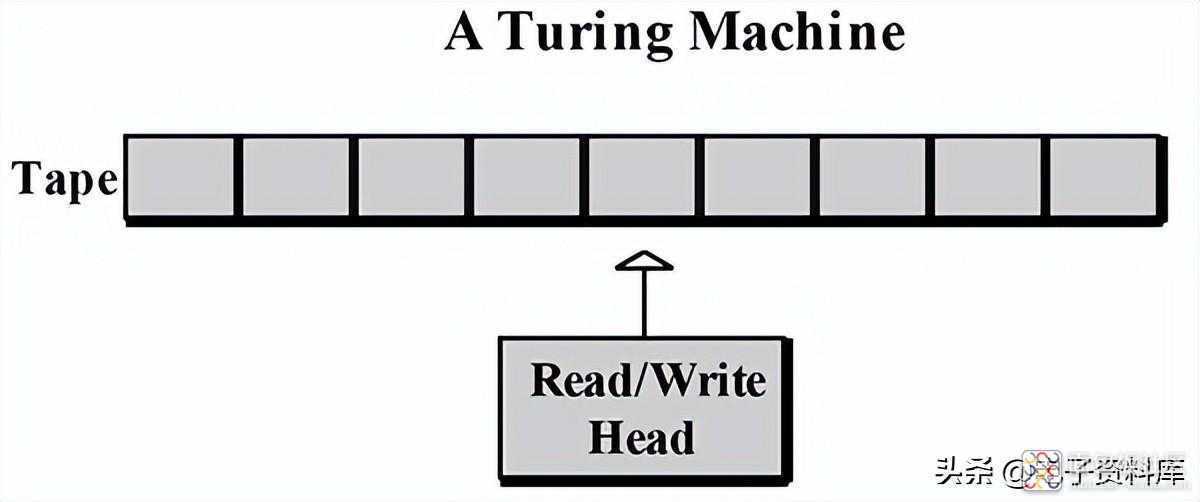
图1。
读/写磁头(有时称为控制磁头)可以读取、写入或擦除其当前所在的磁带段上的符号,但一次只能读取一个段。信不信由你,这种最简单的简单计算机能够完成最强大的超级计算机所能做的任何事情。
如果您研究图灵机,迟早会遇到正式符号。起初它有点吓人,但它确实有用且易于理解。有关图灵机符号的解释,请参见图 2。

图 2。
图灵机的正式定义,表示为 M,是 M = (Q, Σ, Γ, δ, q 0 , B, F)。
含义如下:Q 是一组有限状态,Σ (sigma) 是输入字母表,Γ (gamma) 是磁带字母表,δ (delta) 是转移函数,B 是空白符号,q 0是起始状态,F 为最终状态。希腊字母在理论计算机科学中用作符号约定,就像它们在数学中使用一样。
让我们看一个示例,以便您了解图灵机的工作原理。假设我们有一个胶带,其中填充了符号 a 和 b,并在两端用空白符号框起来,如图 3所示。
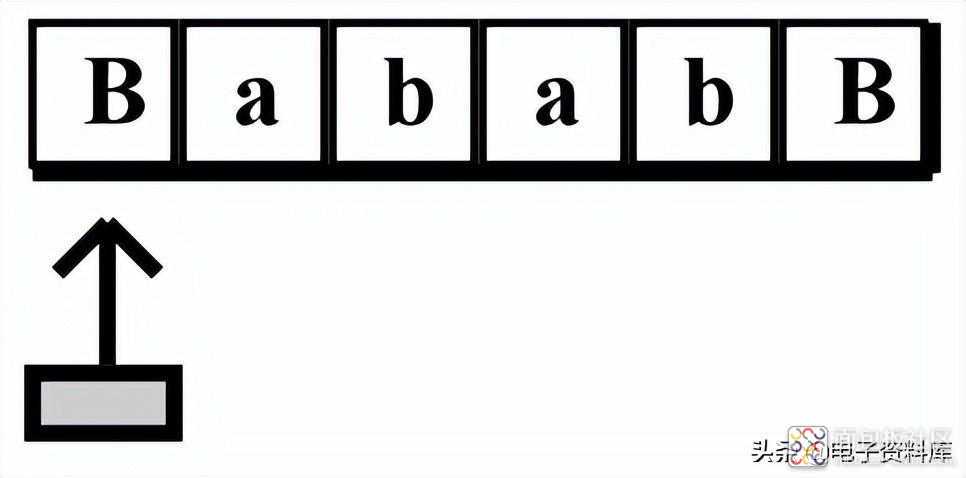
图 3。
我们将在左边的空白处设置起始位置。这是初始状态 q 0。我们希望图灵机做的是将每个 a 更改为 b,将每个 b 更改为 a。我们将此图灵机称为符号交换器。为了对图灵机进行编程以进行符号交换,我们需要开发一组规则或转换函数 δ。以下是英文规则,然后翻译成图灵机符号: 从初始状态 q 0开始。
如果空白在读取头上,则在磁带上重新复制空白,将状态设置为新状态 q 1,并将读取头向右推进。象征性地,我们可以把它写成 (q 0 ,B) = {q 1 , B, R}。一般来说,这意味着 (State, Symbol) = {NewState, NewSymbol, MoveTo}。使用符号,我们可以将冗长的口头描述简化为简短、精确的符号声明。这就是花时间学习和操作符号的价值。
下一步是什么?图灵机现在处于状态 q 1,现在我们希望机器寻找 a 或 b 并交换它们,所以我们需要更多的转换函数。对于状态 q 1,如果 a 在读取头上,则保持状态 q 1,在磁带上写入符号 b,并将头向右推进。这转化为 (q 1 ,a) = {q 1 , b, R}。如果 ab 在读磁头上方,则留在 q 1中,在磁带上写一个 a,然后将磁头向右推进。这转化为 (q 1 ,b) = {q 1 , a, R}。
为了让机器在最终状态 F 中停止,我们还需要一个转换函数。如果空白符号 B 在读取头上方,则停止图灵机。这转化为 (q 1 ,B) = {F}。这个转换函数在执行图灵机时没有正式定义。
为了让图灵机停止,必须有一个未定义的转换,因此读头不能向右或向左前进。图 4列出了描述图灵机的所有转换函数。我们的每个转换都称为一个配置。这是边栏中调用的配置序列 什么是计算?

图 4。
现在我们需要运行图灵机来看看它是否工作。在大多数经典的图灵机文献中,从一个转换到另一个转换的移动由 ( 表示。这个符号表示正在运行的图灵机。图 5显示了我们的图灵机运行时的图形和经典表示。
为任何复杂的图灵机使用图形表示会变得非常麻烦并且占用大量空间,因此您几乎看不到它们。你几乎总是会看到经典的表示。正如您在图 5中看到的,读取头由转换函数 q 0和 q 1表示。读头右侧的符号被认为是读头下方的符号。当读头读取磁带时,它会向右或向左移动并在磁带上重新写入符号。
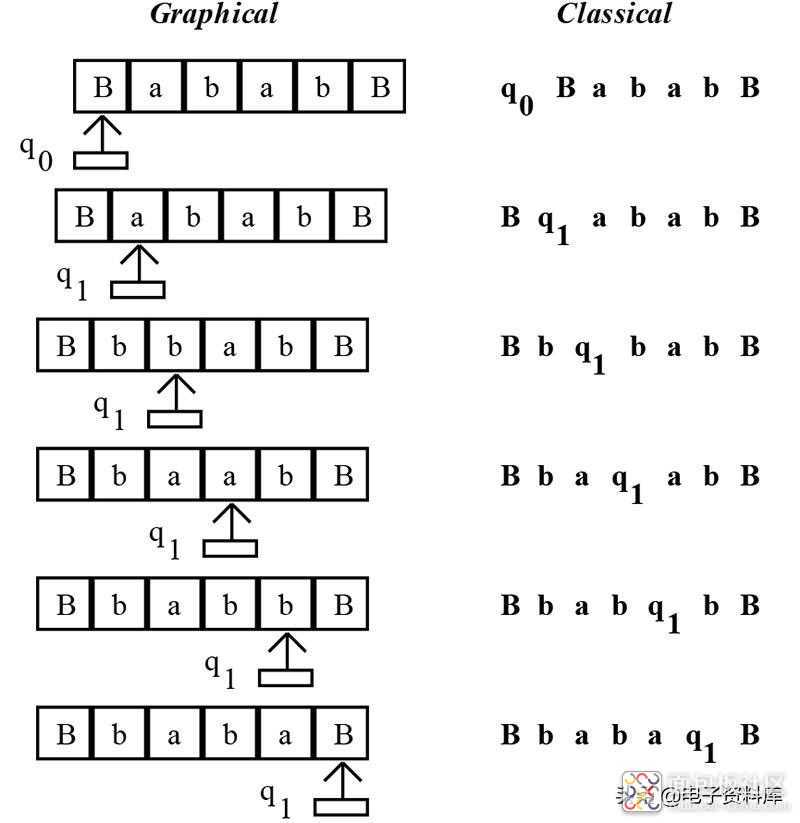
图 5。
所以我们已经证明了将符号 a 更改为符号 b 的图灵机确实有效。那么有什么大不了的呢?好吧,最重要的是,将一个字符转换为另一个字符的算法确实是一种计算,并且由于它在图灵机上正确运行,它应该在宇宙中任何可以想象的计算机上运行!这就是图灵机的深度。
把两个数加起来怎么样?我们直观地知道它确实是一种计算,但你如何证明呢?看看它是否在图灵机上运行!
在磁带上表达数字的一种方法是使用一元格式。在一元格式中,数字二表示为0110。三个一用来表示数字三,零用来分隔数字。数字五是一元格式是 0111110。我们想看看二加二是否是一个计算,所以磁带看起来像 B0110110B(不要忘记磁带充满了空白,所以我们有空白符号达到无穷大胶带的两端)。
我们如何创建一个图灵机来添加这两个一元数?看录像带一会儿。我们想要的结果是 4,即 011110。如果我们可以将最右边的向左移动一位,我们就会得到想要的结果。我们需要的是移位寄存器的一种形式。
图灵机模拟现代计算机的程度令人惊讶,它是在 1936 年发明的!图 6显示了加法器的转换函数,以及使用经典符号的图灵机。通过图灵机模拟器运行它以验证它是如何工作的。

图 6。
图灵机模拟器TMS
图灵机模拟器由三部分组成:输入磁带文件、转换函数文件和 tms.exe 模拟器。输入磁带文件是一个包含磁带字符的 ASCII 文本文件。转换函数文件使用类似于经典图灵机形式的格式。注释也可以通过在行首放置一个 C 来容纳。由于经典的图灵机表示法有点神秘,通常需要自由使用注释(如果你想记住你做了什么!)。一个基本的解析器从源文件中读取转换并将转换加载到结构数组中。
我们真正构建的是一个解释器。转换函数文件是程序源代码,输入磁带文件是数据,tms.exe程序是解释器。读取源代码文件,将源代码分解为单个符号或标记,然后将标记存储在数据结构中的过程称为解析。我们的解析器在函数 ReadTuringMachine() 中。
为了缩短代码长度,ReadTuringMachine() 几乎没有错误检查。这意味着转换函数文件需要相当正确,因为 ReadTuringMachine() 不会检测语法错误。
输入磁带符号被加载到 InputTape[MAX_TAPE_LEN] 数组中。转换函数被加载到一个 TURING_MACHINE 结构数组中。图 7说明了 TURING_MACHINE 结构及其与形式转换函数的关系。

图 7。
图灵机模拟器可以在单步模式下运行,一次执行一个转换,或者在自动模式下,全速执行所有转换功能。符号交换器的输入带、转换函数和计算轨迹如图 8所示。

图 8。
希望这篇文章能让您了解图灵机。这里设计的简单图灵机程序只是一个起点。
有多带图灵机、通用图灵机和许多其他变体。调整 TMS 程序以读取多个磁带将是一个有趣的项目。
有时用图灵机思考可能既困难又费力,但回报是获得对计算基本性质的洞察。编写图灵机并看着它们在模拟器上突飞猛进是很有趣的。
尝试设计一个图灵机来复制字符串或进行其他基本的算术运算,例如减法或乘法。有些机器可能很容易创建,而有些机器可能非常困难。试试看。只需创建一个输入磁带文件和一个转换函数文件。
我通常在输入磁带文件上加上 .dat 扩展名,在转换函数文件上加上 .tm 扩展名。没有命名限制,所以如果你愿意,可以使用你自己的系统。
想了解更多?有很多网站包含有关图灵机的详细、有趣的信息,以及您可以找到通过模拟器运行的大量转换函数。
请记住,在所有科学中,计算机科学仍处于起步阶段。有许多重要的发现有待作出,也有许多重大的问题有待解决。
伟大的发现是从第一原理的框架中产生的。使用第一原理设备,例如图灵机,可能会有所帮助。
来源:电子资料库







 /5
/5 


