matlab工具箱已经成为一个系列产品,matlab主工具箱和各种工具箱,分为通用型和专用型。

Matlab常用工具箱

Matlab常用工具箱
通用型工具箱主要用来扩充matlab的数值计算、符号运算功能、图形建模仿真功能、文字处理功能以及与硬件实时交互功能,能够用于多种学科。而专用工具箱是学科专用工具箱,其专业性很强,比如控制系统工具箱;信号处理工具箱;财政金融工具箱等。
我们以家用空调为例,我们想通过研究空调的制冷效果与用电量之间的关系,从而找到最佳的制冷策略。 那么我们首先需要在实验室,通过试验电机在不同的工作状态下的耗电量并获得大量的基础数据,由于测量误差的存在,可能这些数据建立的方程式相互冲突还无法直接求解。如果我们有一个工具箱把所有需要进行复杂的计算过程组装成一个简单的命令,而这个命令就能帮我们将实验数据模拟出一个函数,使得这个函数与所有的数据结果都很接近(专业术语为拟合)的话,岂不美哉。
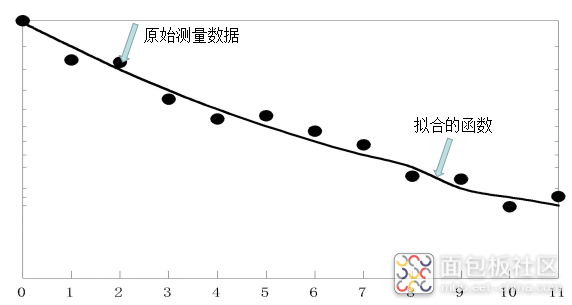
线型拟合

学科前沿最新的工具箱
而这就是工具箱的魅力,通过将一定的基础算法整合到一起,只需要输入几个简单的命令就能完成大量复杂的数学运算和数据处理,甚至我们使用者只需要知道这个工具箱的应用无需知道底层的逻辑依然能够出色的完成任务,这是不是加快了项目的研发进程降低了研发的门槛?这样的工具箱谁又不希望拥有呢。
来源:土豆说科普
Matlab的优化工具箱(Optimization Toolbox)中含有一系列的优化算法,用于求解不同的优化问题,由一些对普通非线性函数求解最小化或最大化极值的函数和解决诸如线性规划等标准矩阵问题的函数组成。
作者:郑铿城,经济学博士,数学建模指导教练
MATLAB优化工具箱拥有以下4类求解器:
1.最小值优化
这一组求解器用于求解目标函数在初始点x0附近的最小值位置。适用于无约束优化、线性规划、二次规划和一般的非线性规划。
2.多目标最小值优化
这一组求解器用于求解一组方程极大值中的极小值(fminimax),还可以求解一组方程低于某一特定值的定义域(fgoalattain)。
3.方程求解器
这一组求解器用于求解一个标量或者向量非线性方程f(x) = 0在初始点x0附近的解。也可以将方程求解当作是一种形式的优化,因为它等同于在x0附近找到一个f(x)模的最小值。
4.最小二乘(曲线拟合)求解器
这一组求解器用于求解一组平方和的最小值。这样的问题常在求一组数据的拟合模型的过程中出现。这组求解器适用于求问题非负解、边界限定或者线性约束解问题,还适用于根据数据拟合出参数化非线性模型。
为此,我们应根据自己的实际需要,根据实际的约束条件来选择相应的求解器。4种求解器所对应的所有优化函数如所示。
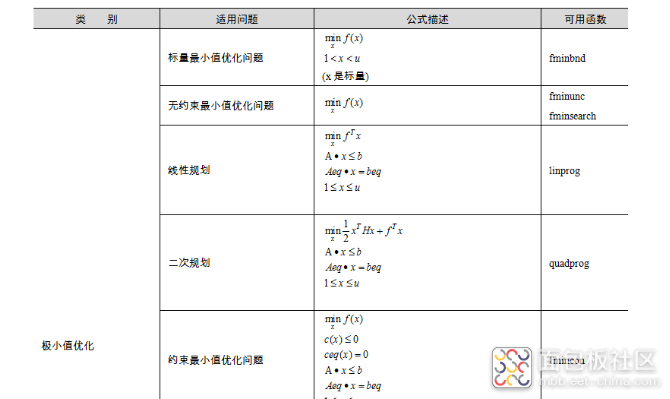



极小值优化
标量最小值优化
求解单变量最优化问题的方法有多种,根据目标函数是否需要求导,可以分为两类,即直接法和间接法。直接法不需要对目标函数进行求导,而间接法则需要用到目标函数的导数。
常用的一维直接法主要有消去法和近似法两种。
消去法:该法利用单峰函数具有的消去性质进行反复迭代,逐渐消去不包含极小点的区间,缩小搜索区间,直到搜索区间缩小到给定的允许精度为止。一种典型的消去法为黄金分割法(Golden Section Search)。黄金分割法的基本思想是在单峰区间内适当地插入两点,将区间分为3段,然后通过比较这两点函数值的大小来确定是删去最左段还是最右段,或同时删去左右两段,而保留中间段。重复该过程可以使区间无限缩小。插入点的位置放在区间的黄金分割点及其对称点上,所以该法称为黄金分割法。该法的优点是算法简单,效率较高,稳定性好。
多项式近似法:该法用于目标函数比较复杂的情况。此时搜索一个与它近似的函数代替目标函数,并用近似函数的极小点作为原函数极小点的近似。常用的近似函数为二次和三次多项式。二次插值法的计算速度比黄金分割法快,但是对于一些强烈扭曲或可能多峰的函数,该法的收敛速度会变得很慢,甚至失败。
间接法需要计算目标函数的导数,优点是计算速度很快。常见的间接法包括牛顿切线法、对分法、割线法和三次插值多项式近似法等。优化工具箱中用得较多的是三次插值法。如果函数的导数容易求得,一般来说应首先考虑使用三次插值法,因为它具有较高的效率。在只需要计算函数值的方法中,二次插值法是一个很好的方法,它的收敛速度较快,特别是在极小点所在区间较小时尤为如此。黄金分割法则是一种十分稳定的方法,并且计算简单。基于以上分析,MATLAB优化工具箱中使用得较多的方法是二次插值法、三次插值法、二次三次混合插值法和黄金分割法。
MATLAB优化工具箱提供了fminbnd函数来进行标量最小值问题的优化求解。

无约束最小值优化
无约束最优化问题在实际应用中也比较常见,如工程中常见的参数反演问题。另外,许多有约束最优化问题也可以转化为无约束最优化问题进行求解。
求解无约束最优化问题的方法主要有两类,即直接搜索法(Search method)和梯度法(Gradient method)。
直接搜索法适用于目标函数高度非线性,没有导数或导数很难计算的情况。实际工程中很多问题都是非线性的,因此直接搜索法不失为一种有效的解决办法。常用的直接搜索法为单纯形法,此外还有Hooke-Jeeves搜索法、Pavell共轭方向法等,其缺点是收敛速度慢。
在函数的导数可求的情况下,梯度法是一种更优的方法,该法利用函数的梯度(一阶导数)和Hessian矩阵(二阶导数)构造算法,可以获得更快的收敛速度。函数f(x)的负梯度方向即反映了函数的最大下降方向。当搜索方向取为负梯度方向时,称为最速下降法。但当需要最小化的函数有一狭长的谷形值域时,该法的效率则很低。常见的梯度法有最速下降法、Newton法、Marquart法、共轭梯度法和拟牛顿法(Quasi-Newton method)等。在这些方法中,用得最多的是拟牛顿法。
在MATLAB中,有fminunc和fminsearch两个函数用来求解无约束最优化问题。

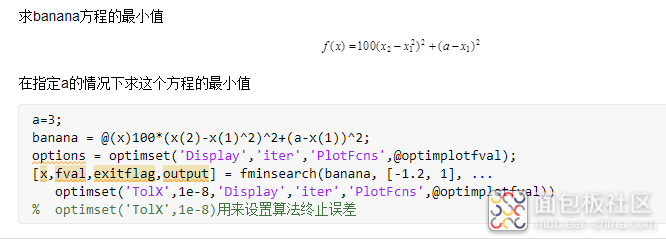
线性规划
线性规划是处理线性目标函数和线性约束的一种较为成熟的方法,目前已经广泛地应用于军事、经济、工业、农业、教育、商业和社会科学等许多方面。
线性规划的标准形式要求目标函数最小化,约束条件取等式,变量非负。不符合这几个条件的线性模型要首先转换成标准形。线性规划的求解方法主要是单纯形法。
MATLAB优化工具箱提供了linprog函数用来进行线性规划的求解
linprog函数适用的线性规划问题标准形式为:
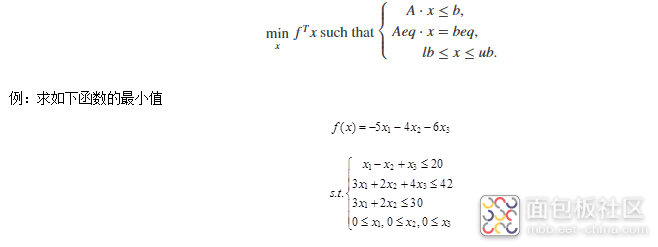

Lambda域中向量里的非零元素可以反映出求解过程中的主动约束。在本例的结果中可以看出,第2个和第3个不等式约束(lambda.ineqlin)和第1个下界约束(lambda.lower)是主动约束。
二次规划
二次规划是非线性规划中一类特殊的数学规划问题,它的解是可以通过求解得到的。通常通过解其库恩-塔克条件(K-T条件),获取一个K-T条件的解,称为K-T对,其中与原问题的变量对应的部分称为K-T点。二次规划的一般形式为:
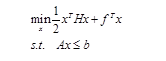


exitflag = 1表示计算的退出条件是收敛于x。output是包含着优化信息的结构数组。lambda返回了x处包含拉格朗日乘子的参数。
有约束最小值优化
在有约束最优化问题中,通常要将该问题转换为更简单的子问题,对这些子问题可以求解并作为迭代过程的基础。早期的方法通常是通过构造惩罚函数等,将有约束的最优化问题转换为无约束最优化问题进行求解。现在,这些方法已经被更有效的基于K-T方程解的方法所取代。K-T方程是有约束最优化问题求解的必要条件。
MATLAB优化工具箱提供了fmincon函数用来计算有约束的最小值优化。

x0 = [10; 10; 10]; % 求解的起始点
A=[-1 -2 -2;1 2 2];
b=[0;72];
[x,fval] = fmincon(@myfun3,x0,A,b)
A*x-b %对约束条件进行验证
多目标优化
前面介绍的最优化方法只有一个目标函数,是单目标最优化方法。但是,在许多实际工程问题中,往往希望多个指标都达到最优值,所以就有多个目标函数,这种问题称为多目标最优化问题。
多目标规划有许多解法,下面列出常用的几种。
化多为少法:将多目标问题化成只有1个或2个目标的问题,然后用简单的决策方法求解。最常用的是线性加权和法。
分层序列法:将所有的目标按其重要程度依次排序,先求出第1个(最重要的)目标的最优解,然后在保证前一个目标最优解的前提下依次求下一个目标的最优解,一直求到最后一个目标为止。
直接求非劣解法:先求出一组非劣解,然后按事先确定好的评价标准从中找出一个满意的解。
目标规划法:当所有的目标函数和约束条件都是线性时,可以采用目标规划法,它是20世纪60年代初由查纳斯和库珀提出来的。此方法对每一个目标函数都事前给定一个期望值,然后在满足约束条件集合的情况下,找出使目标函数离期望值最近的解。
多属性效用法(MAUM):各个目标分别用各自的效用函数表示,然后构成多目标综合效用函数,以此来评价各个可行方案的优劣。
层次分析法:由T.沙基于1980年提出来。这种方法是通过对目标、约束条件、方案等的主观判断,对各种方案加以综合权衡比较,然后评定优劣。
重排次序法:把原来不好比较的非劣解,通过其他办法排出优劣次序。此外,还有多目标群决策和多目标模糊决策等方法。
针对多目标优化问题,MATLAB提供了fgoalattain和fminimax 函数用来进行求解。
例:
某工厂因生产需要欲采购一种原材料,市场上这种原材料有两个等级,甲级单价2元/千克,乙级单价1元/千克。要求所花总费用不超过200元,购得原材料总量不少于100千克,其中甲级原材料不少于50千克,问如何确定最好的采购方案。
设x1、x2分别为采购甲级和乙级原材料的数量(千克),要求总采购费用尽量少,总采购重量尽量多,采购甲级原材料尽量多。
myfun4.m
function f=myfun4(x)
f(1)=2*x(1)+ x(2);
f(2)=-x(1)- x(2);
f(3)=-x(1);
goal=[200 -100 -50]; % 要达到的目标
weight=[2040 -100 -50]; % 各个目标的权重
x0=[55 55]; % 搜索的初始值
% 约束条件
A=[2 1;-1 -1;-1 0];
b=[200 -100 -50];
lb=zeros(2,1);
% 调用fgoalattain函数进行多目标优化
[x,fval,attainfactor,exitflag] =...
fgoalattain(@myfun4,x0,goal,weight,A,b,[],[],lb,[])
方程组求解
优化工具箱提供了3个方程求解的函数,其中,“\”算子可用于求解线性方程组Cx=d。当矩阵为n阶方阵时,采用高斯消元法进行求解;如果A不为方阵,则采用数值方法计算方程最小二乘意义上的解。fzero采用数值解法求解非线性方程,fsolve函数则采用非线性最小二乘算法求解非线性方程组。

x0 = [-5; -5]; % 猜测的搜索初始值
options=optimset('Display','iter'); % 输出显示选项设置
[x,fval] = fsolve(@myfun5,x0,options) % 调用fsolve命令
最小二乘及数据拟合
最小二乘法是一种数学优化技术,它通过最小化误差的平方和找到一组数据的最佳函数匹配。最小二乘法通常用于曲线拟合。很多其他的优化问题也可以通过最小化能量或最大化熵用最小二乘形式表达。
MATLAB中提供了多个函数用来计算最小二乘问题,如\、lsqnonneg、lsqlin、lsqnonlin、lsqcurvefit等
求超定系统C·x = d的最小二乘解,约束条件为A·x≤b,lb≤x≤ub(具体的系数矩阵、边界条件如下所示)。
首先输入系数矩阵和上下边界。
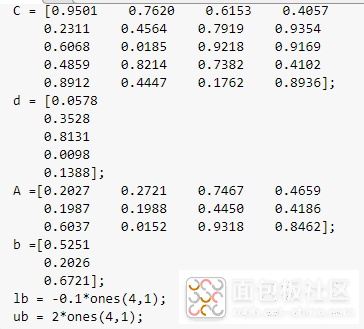
然后调用约束最小二乘lsqlin函数:

lambda结构数组中向量的非零元素可以说明解的主动约束条件。在本例中,第2个不等式约束和第1个、第2个下界边界约束是主动约束。

x0 = [0.3 0.4] % 初始值
[x,resnorm] = lsqnonlin(@myfun6,x0) % 调用优化命令
以上就是优化工具箱的使用,可以在实践中多多运用!






 /3
/3 
