前一篇讨论了傅立叶级数的几何结构与组成，属于二维结构，本篇用空间三维模型来描述它的立体结构，需要结合上一篇才会更加形象直观。
这是取自国外数学家所做的视频，有必要的单独做个说明，供学习参考。
sinθ函数的立体空间模型：底面是XY坐标系，Z轴是随时间变化的wt轴，即角度
当圆旋转时就是：
2cc9c8f6b91c415e8114872490d400ab~noop.image?_iz=58558&from=article.jpg
侧面看
bc2a56ea21a9485aa7122a9c739095b2~noop.image?_iz=58558&from=article.jpg
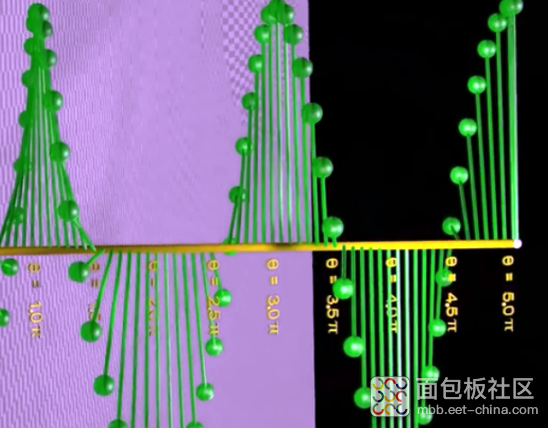
所以sinθ函数在空间上的图形就是螺旋线：
4c8a036ffb064e24b1967e2768dffc51~noop.image?_iz=58558&from=article.jpg
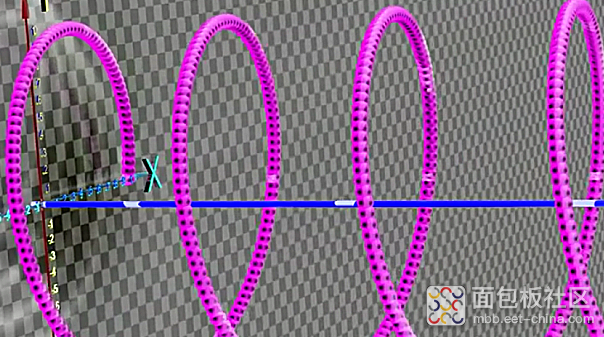
螺旋线ZY平面上的投影
b2518abfff694433934ad45eb36e9931~noop.image?_iz=58558&from=article.jpg
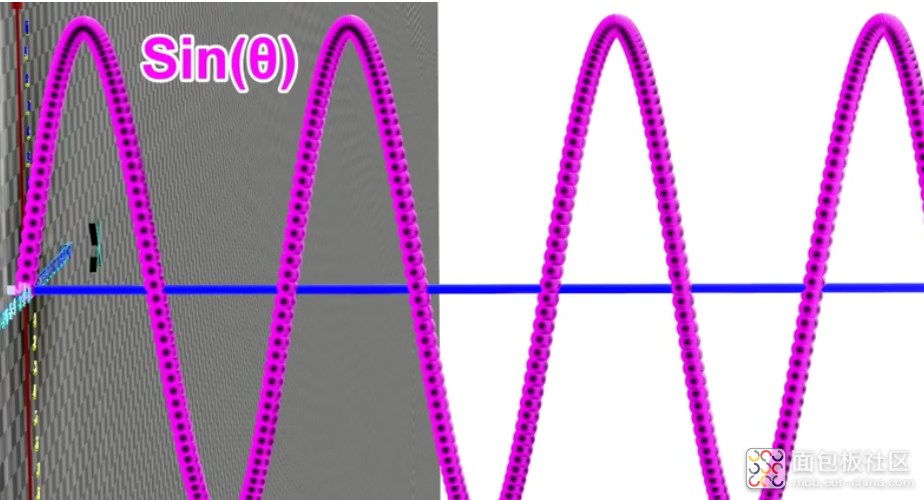
伙伴们可以想下，螺旋线在水平面XZ上的投影就是余弦函数，所以螺旋线就是正弦函数和余弦函数在空间上的叠加
如下是两个相位相同的正弦波叠加模型：会看到等于sinθ。
d659343ce84b42c4a1ea990c5514f3fb~noop.image?_iz=58558&from=article.jpg
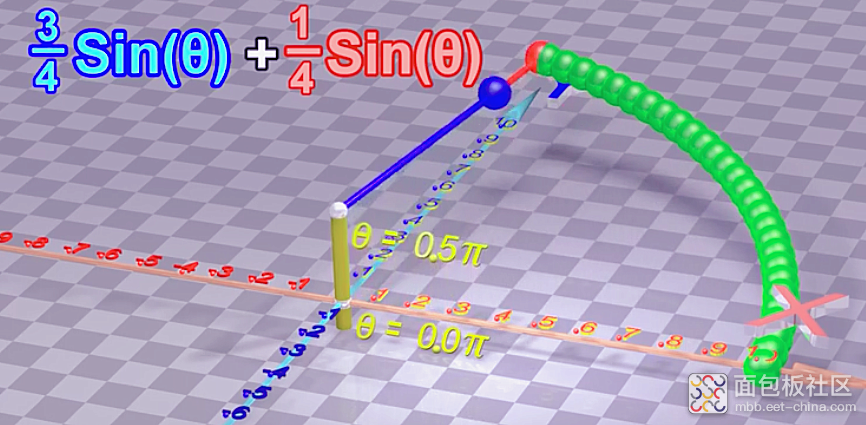
波形拆解开来就是：
0ede9d6cc3724c81a1722d2e84dffdd6~noop.image?_iz=58558&from=article.jpg
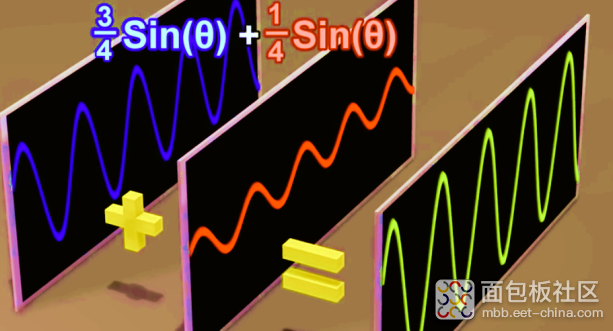
改变其中的一个相位角，相位出现片偏差时，如下红色杆和蓝色杆就不在一条直线上了，图形是
058658fd3e9f4ce795201b5008dc9a4d~noop.image?_iz=58558&from=article.jpg
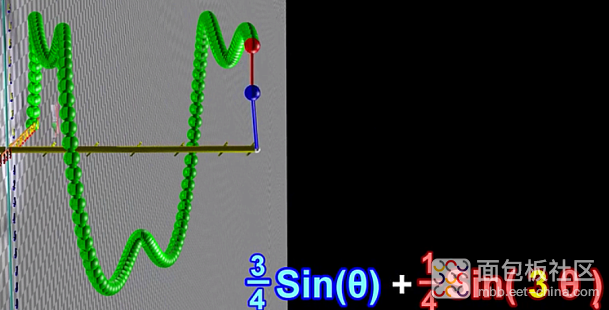
叠加的图形就是两个三角函数单独运作的叠加图形，也是空间模型在YZ上的投影
612117c2e54f4369978512029c1cc0c9~noop.image?_iz=58558&from=article.jpg
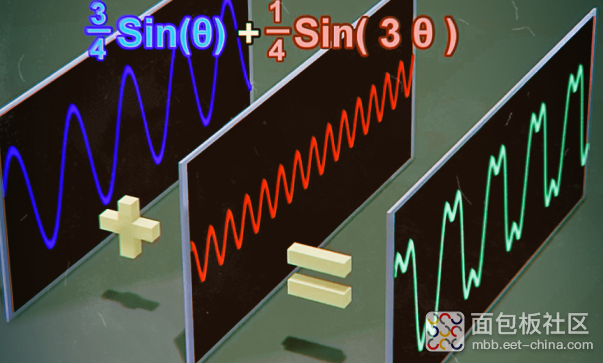
叠加更多相位角不同的正弦波
3f0d188f7da042efafd80ee989f9c39d~noop.image?_iz=58558&from=article.jpg
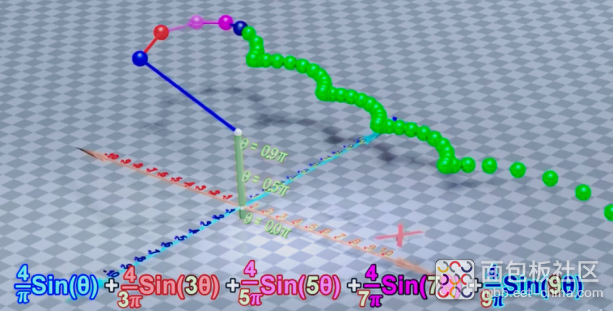
图形就是所有三角函数单独运作的叠加图形
9eb3c44de3a2400b8aebdfbe63321f5f~noop.image?_iz=58558&from=article.jpg
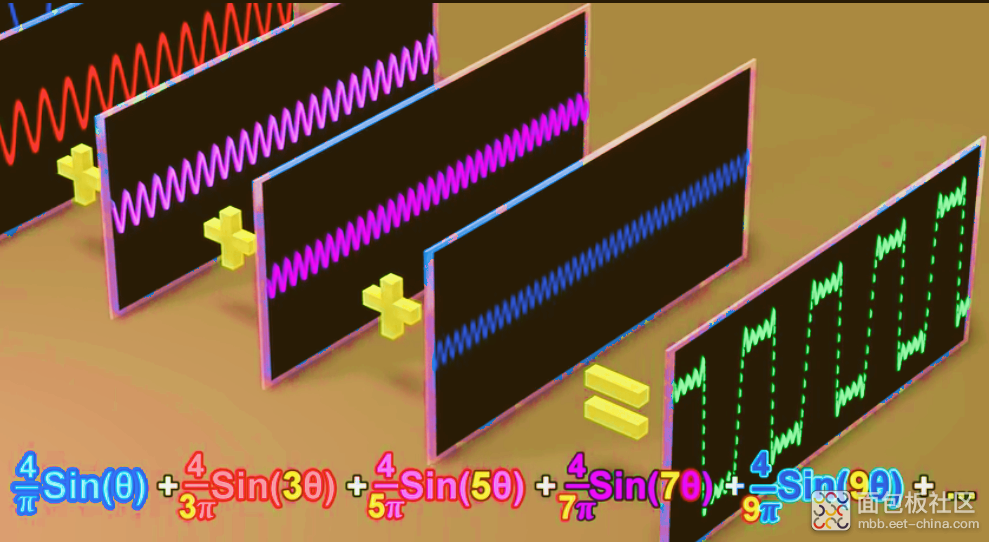
项数越多图形越精确，叠加的模型也正是空间模型在YZ平面上的投影​
4713d722b23343deb929c4b24a50d417~noop.image?_iz=58558&from=article.jpg
这正是方波的图形原理
ae8d06b56a044ba0bdd34212647adefa~noop.image?_iz=58558&from=article.jpg
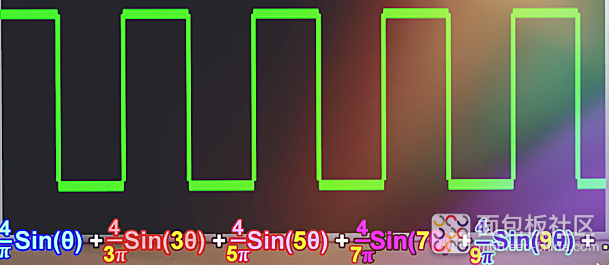
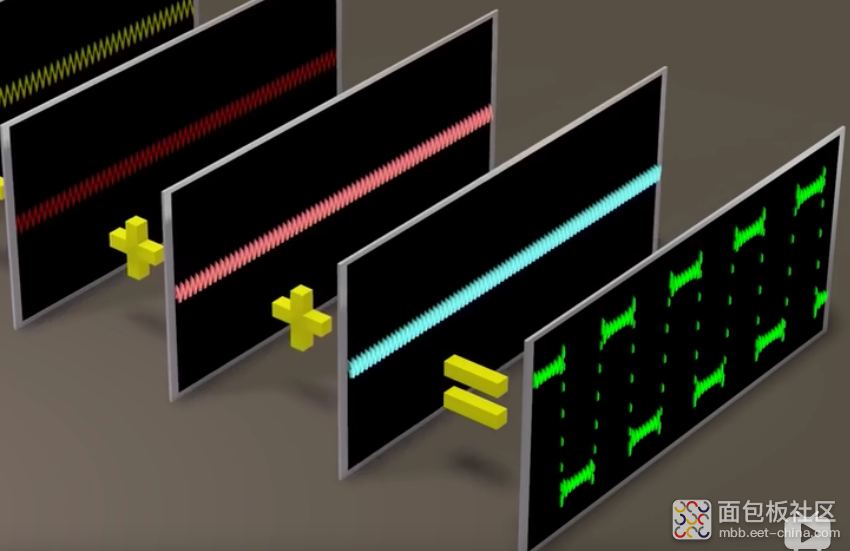
三角波的图形：各个正弦波相位角不同
2460efdce04b41ed907f6e0aea924f2d~noop.image?_iz=58558&from=article.jpg
4469e701e530403db4919df8373d0fcf~noop.image?_iz=58558&from=article.jpg
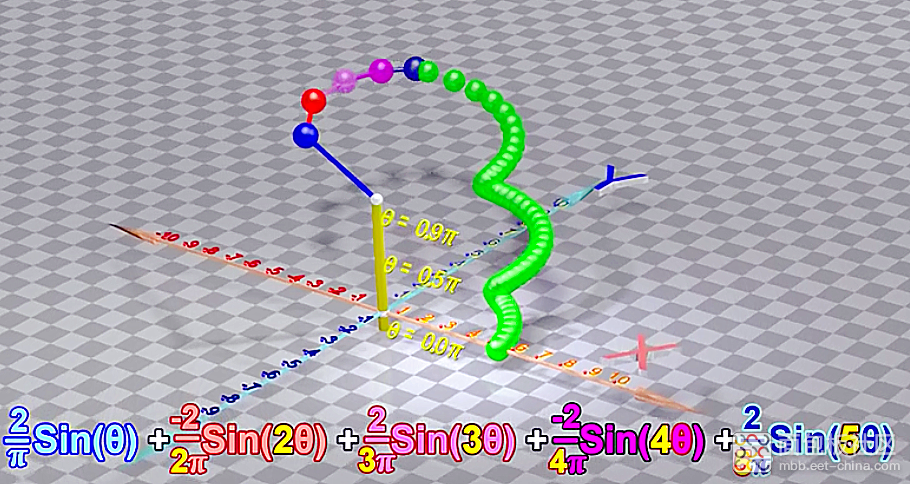
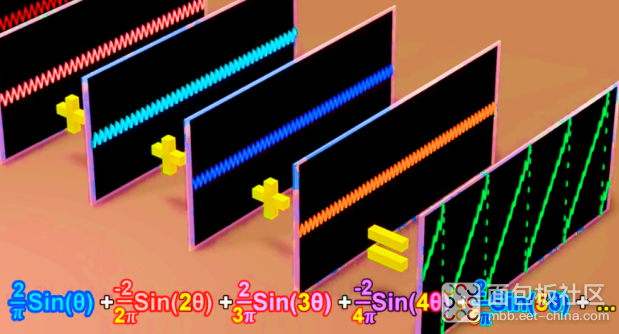
以上就是对傅立叶级数在空间模型上的可视化拆解