昨天看到了一篇TI的技术文章,里面提到了一个比较有意思的电路,就是用多路PWM并联来提高PWM-DAC的输出精度。比如组合两路8bit的PWM来组合为16bit的PWM-DAC。
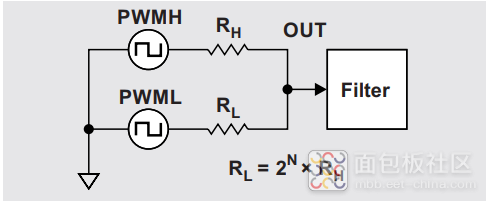
理论:
那么先解释一下PWM的精度问题(因为PWM的占空比精度直接关联到PWM做DAC应用时的DAC精度)。
举一个例子:如果要产生10kHz的PWM波形,而分别提供50Mhz的时钟和10Mhz的PWM外设时钟,那么毋庸置疑的是均可以产生10Khz的波形。但是如果要调整这个波形的占空比,从0%到100%,那么在PWM时钟为50Mhz的时候,可以调整出5000步,而在时钟为10Mhz的情况下,只能调整出1000步。
那么如果在上述的例子中,时钟为10Mhz的情况下,如果想要保持分辨率为5000,那么就要改变PWM的频率,把频率降低为2Khz就可以满足5000的分辨率。然而在降低PWM频率的时候会随之带来另一个问题,那么就是转化出的DAC的纹波变大了(因为滤波器参数没变,PWM的频率降低后,滤波器对PWM的高次谐波的衰减变弱了)。那么为了维持转化后DAC的纹波,就要调低滤波器的截止频率。如下图所示,滤波器和PWM的傅里叶变换后高次谐波的关系。
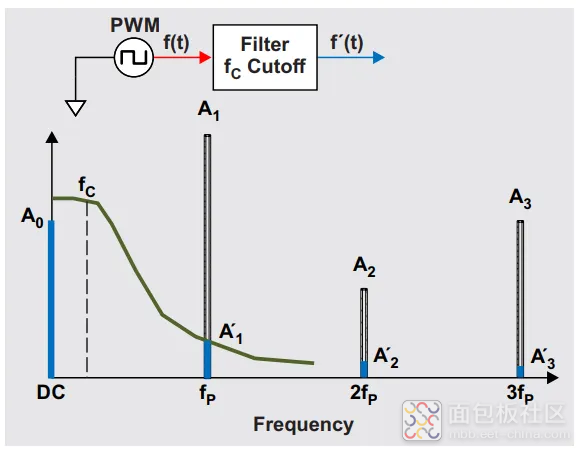
但是由RC滤波器的公式

那么有什么方法可以在保持时钟和频率以及建立时间都不改变的情况下来提高PWM-DAC的分辨率呢?此时就可以使用多个PWM叠加,这种方法来提高转化DAC分辨率的电路,简图如下:
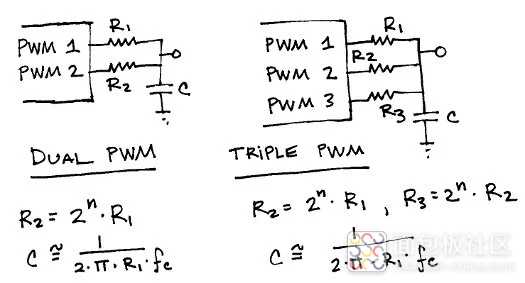
仿真如下:
首先使用信号发生器输出PWM频率为100Khz,假定PWM分辨率为10(即PWM占空比的调节步长为10%)那么如果只用一路PWM转DAC的话,输出DAC的电压只能是0.1*VCC,0.2*VCC,0.3*VCC一直到VCC,DAC输出也是10%步进,和PWM的精度(10%步进)是完全一致的。例如下图仿真,幅值为10V的占空比为40%的PWM信号经过滤波器后输出的电压为4V。这个10V幅值PWM步进10%的话,这个电路的输出电压只能是随着占空比的10%步进而输出0V,1V,2V,3V,4V.....10V(1V精度)。
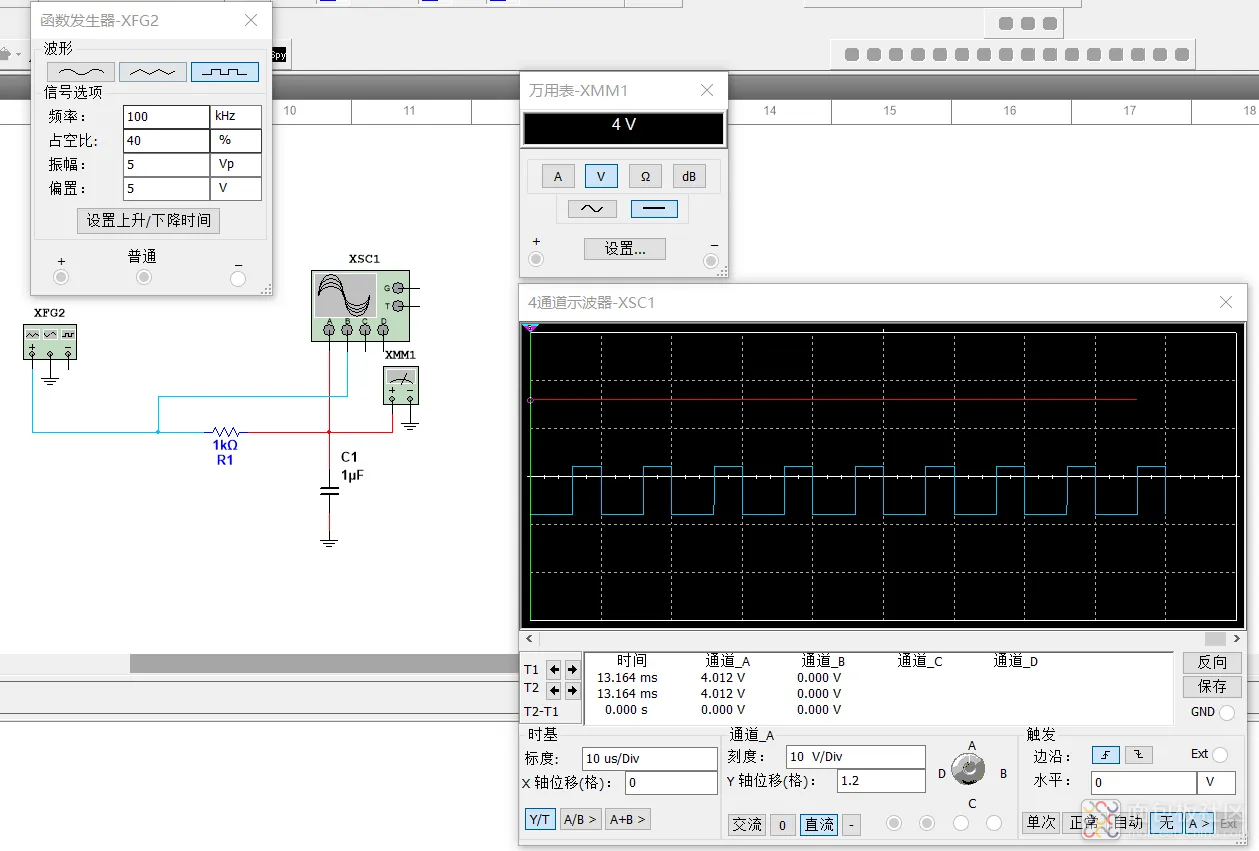
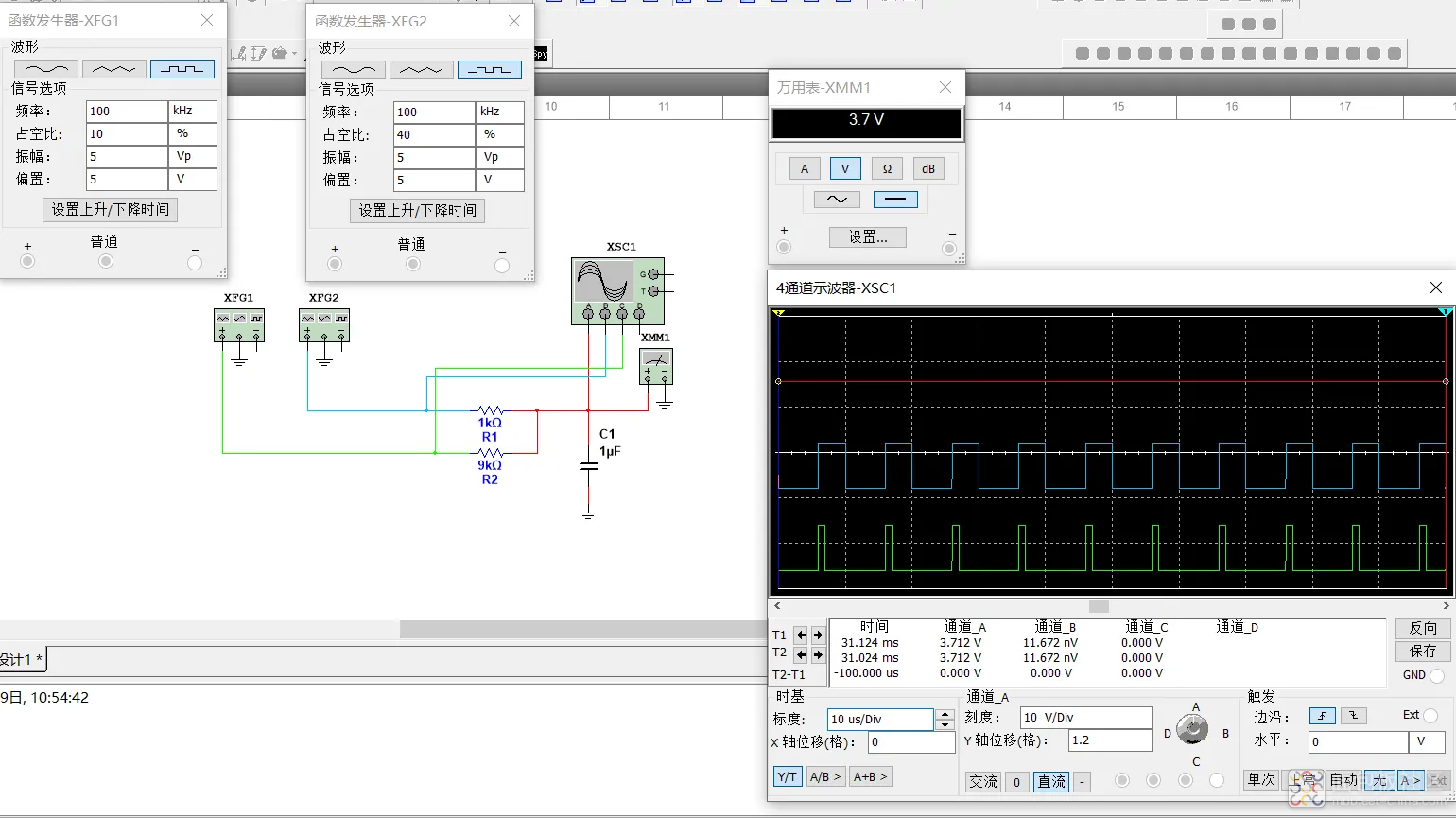
那么假如此时按照TI的思路,再并联一路PWM过去会如何呢?此时绿色信号发生器XFG1的输出PWM1便可以代表DAC的低位(即TI技术文档中的PWML信号),蓝色信号发生器XFG2的输出PWM2便代表DAC的高位(即TI技术文档中的PWMH信号),那么整个电路便可以输出0-10V(1%步进,0.1V精度),输出电压公式可以列为:VXFG2*0.9+VXFG1*0.1(可以用叠加定理求取)。下图仿真的电压为:
10V*40%*0.9+10V*10%*0.1=3.7V
便以此实现了1%的步进精度,提高了DAC的输出。





 /5
/5 


