举个例子,考虑图1 (a)所示的常规比例积分控制器(PI)。 P部分和 I 部分采用相同的反馈信号工作,意味着该信号的动态特性必须适合两种控制路径。不过,P路径和I路径可以分离,如图1 (b)所示。由此还可以再前进一小步,图1 (c)显示P路径和I路径分离,并且采用具有不同动态特性的反馈信号工作。

图1. PI控制器方案
*(a)常规方案
*(b) P路径和I路径分离
*(c) P路径和I路径分离且反馈分离
P部分的任务是抑制快速负载变化和快速速度变化,但精度不是主要考虑。换言之,低抽取率和短延迟的sinc滤波器对P部分有利。I部分的任务是确保稳态性能稳定且精确,它要求高精度。因此,高抽取率和较长延迟的sinc滤波器对I部分有利。这就产生了图2所示的实现方案。

图2. 双sinc滤波器和分离的电流控制器 P 路径和 I 路径
电机相电流由一个传感器(分流电阻)测量,并流经一个抗混叠滤波器,供应给Σ-Δ ADC。然后,1位数据流输入两个sinc滤波器,一个针对P控制器调谐,另一个针对I控制器调谐。
为了评估电流反馈分为两条路径的影响,我们对该闭环执行了稳定性分析。对于传统的Z域分析,sinc滤波器会带来问题。它会引入一个延迟,对于任何实际抽取率,该延迟小于一个采样周期。例如,若系统以fsw = 10 kHz的速率运行,滤波器延迟将短于100 μs。从控制环路方面看,sinc模块是一个小数延迟滤波器。为了模拟小数延迟,将sinc滤波器近似看作一个全通滤波器。在最高为奈奎斯特频率一半的较低频率时,该近似处理是精确的,但在更高的频率,其与理想滤波器有一些偏差。然而,这里的目的是了解双反馈如何影响环路稳定性,就此而言,该近似是合适的。
作为对比,图3(a)显示了反馈路径(无双反馈)中仅使用一个sinc滤波器时的闭环幅度响应。开关频率fsw为10 kHz,奈奎斯特频率设置为5 kHz。在这些系统参数下,对于0 μs至80 μs的sinc滤波器群延迟,绘制闭环响应曲线。注意,群延迟与抽取率直接相关。同预期一样,低抽取率和群延迟对闭环稳定性的影响很小,但随着延迟增加,系统阻尼变得越来越小。
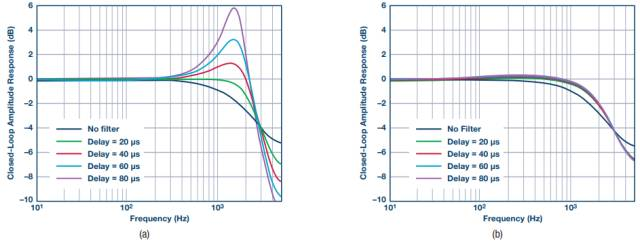
图3. 双反馈对电流控制性能的影响,(a) sinc滤波器为P控制器和I控制器共用,(b) P控制器和I控制器分别使用单独的sinc滤波器
现在将反馈分离,使P控制器和I控制器具有单独的路径,便可获得图3 (b)。这种情况下,用于P控制器的sinc滤波器抽取率是固定值,使得群延迟为10 μs。仅I控制器的抽取率发生变化。
从图3 (b)可看出,提高I控制器的延迟对闭环稳定性的影响非常小。如上所述,可利用这些特性来提高环路的动态和稳态性能。
本文中,使用分离反馈的算法为PI控制器。不过,这只是一个例子,大多数控制系统都有多个算法,根据动态和精度要求调谐反馈对这些算法是有利的。磁通观测器、前馈控制器和PID控制器的差分部分就是一些例子。
来源:ADI




 /5
/5 

