本文针对微带线拐角进行了详细仿真,证明了广为流传的“3W规则”并非性能最优的处理方式。同时,我们通过仿真优化,提供了其他的方案以供性能指标要求高的场合参考使用。
什么是微带不连续?
微带线作为一种最常见的平面传输线,自上世纪60年代以来已广泛应用在射频电路中。图1表示了微带线结构示意图。其中W表示微带线宽度,t表示微带线厚度,h表示微带线到参考地之间的介质厚度,εr表示介质的介电常数。
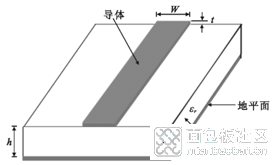
图1 微带线结构示意图
实际电路布线时,由于印刷板大小的限制,常需要做弯折走线处理,即在PCB中会出现微带线拐角,它属于典型的微带线不连续结构之一[1]。文献[1]给出了微带线直角折弯的等效模型,如图2所示,详细的等效推导请查阅文献[1]。由于微带电路尺寸与工作波长可以相比拟,所以这种不连续性会引入寄生电抗,从而引起相位和振幅误差、输入与输出的失配,以及可能存在的寄生耦合,进而导致电路性能的恶化,影响PCB电路信号的传输特性。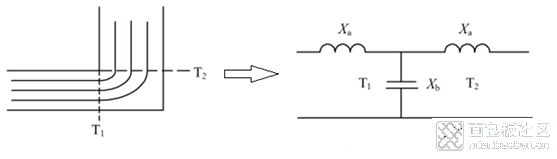
图2 微带线直角折弯示意图及等效模型
以2.4G频段为例,低成本设计中常使用普通FR4板材,并贴装0402封装的电容或电感进行阻抗匹配,为减小实际使用中微带线与元器件焊接的不连续,微带线线宽尽量接近0.5mm(0402封装宽度)。使用AWR公司的TXline软件计算特性阻抗为50Ω传输线的结构参数,依此为初始值,再使用Ansoft HFSS软件对直线进行仿真,寻找出反射最小时的结构参数,最终计算参数为:
t=0.035mm(1oz铜厚)
h=0.275mm(≈10mil)
εr=4.4,W=0.484mm
仿真结果如图3所示,当W=0.484mm时,反射系数S11=-43.26dB,图中两条曲线分别表示理论线宽与优化后的线宽反射系数S11,左上角标注了2.4G频段的反射系数读数,右上角显示了HFSS仿真模型。相对于理论计算结果W=0.5mm,仿真结果表明经HFSS仿真优化后,S11减小了约13dB。
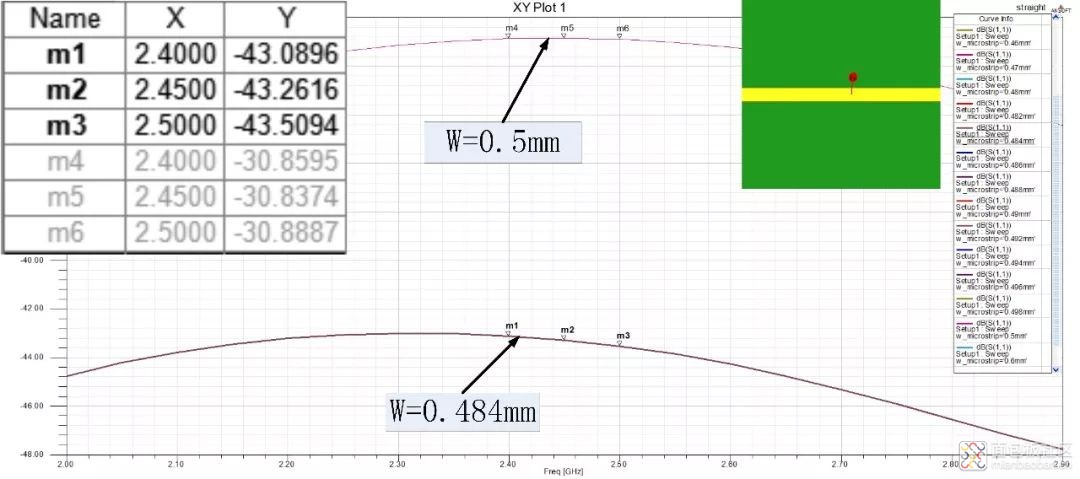
图3 微带线直线仿真结果
使用以上参数对直角折弯进行了仿真,仿真结果如图4所示,明显看出,微带线直角折弯比直线的反射增大了约14dB,达到了-29.82dB。
注:为排除线长影响,本文所有仿真模型中,微带线总长度相等(50mm)。
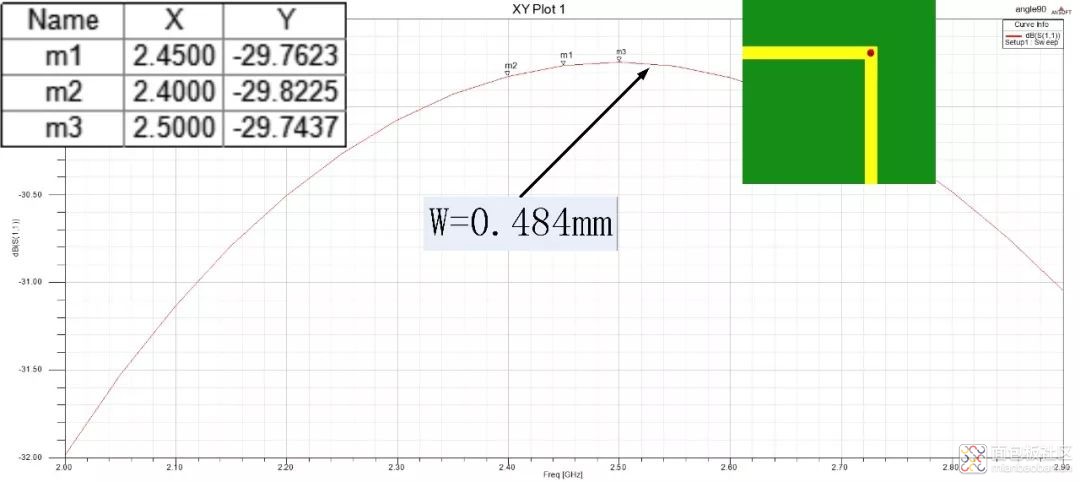
图4 直角折弯仿真结果
你要的“3W规则”
为了减小微带线反射,可能会有很多工程师告诉你:遵循3W规则。
3W规则是什么呢?3W规则表示使用半径大于3倍线宽W的圆弧进行拐弯,能使得转弯处线宽变化较小,从而减小不连续性,在微带线上称之为“扫掠弯头”,如图5所示。
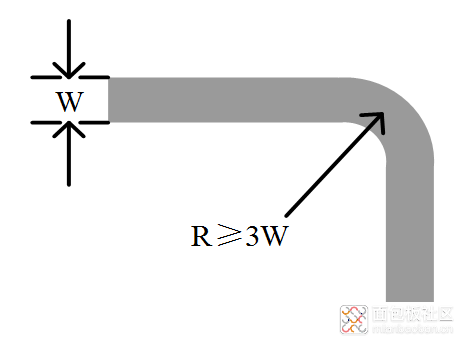
图5 扫掠弯头示意图
对该结构进行电磁仿真,仿真结果如图6所示。当扫掠弯头半径R=3W时,S11=-34.6dB,当R=4W时,S11反而增加,直到R=11W时,扫掠弯头的S11才能降到很低,达到-40.03dB。此时就可以解释文章开篇提出的疑惑之一:为什么是3W?是因为R=3W时,S11值已经能满足多数使用要求,如果再增加R(比如R=4W),性能反而稍差,直到R增加到很大才能使得性能指标接近于直线,但此时将占用很大的PCB空间,这在集成度越来越高的PCB布局中是不能接受的。
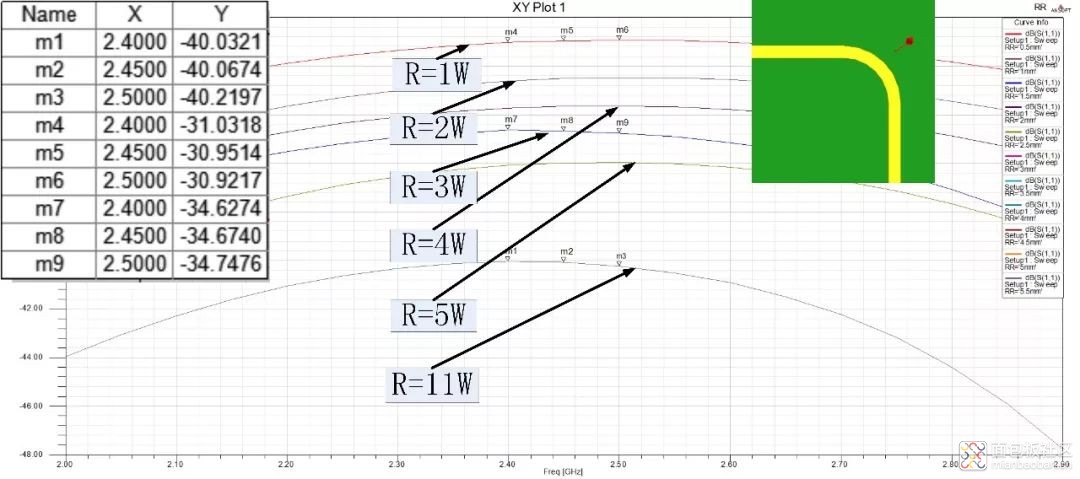
图6 扫掠弯头仿真优化结果
不妨试试直角弯曲45°外斜切
文献[2]提供了其他几种微带不连续性补偿的几种方案,文献[3]、[4]、[5]以实验方法和数值方法详细分析了不同结构的微带线直角弯曲的信号传输特性, 对微带线进行切角处理可以减小拐角处的等效电容,从而补偿微带线直角弯曲的不连续性效应,理论上这种方法可应用于任意张角的拐角。文献中指出微带线直角弯曲45°外斜切结构形式能够很好地改善信号传输特性且存在最佳斜切率。
直角弯曲45°外斜切结构形式如图7所示,图(a)中d 表示微带线直角弯曲内拐角至外拐角的距离,x 表示45°外斜切处至外拐角的距离,并定义外斜切率:m=(x/d)×100 ,当m=0 时意味着微带线直角弯曲外拐角没有被切割,而m=100 时意味着微带线直角弯曲外拐角被完全切割,把微带线从弯曲处分成了两部分。
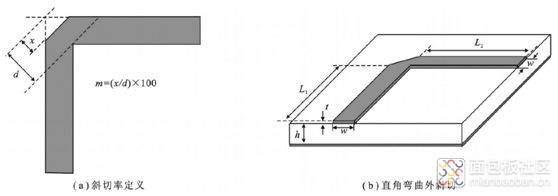
图7 直角弯曲45°外斜切示意图
本文对此种方案也进行了仿真,仿真结果如图8。当斜切率=80时,S11=-41.492dB,反射最小,说明本方案经过优化能得到比“3W规则”更好的性能。对比文献[3]、[4]、[5]中的经验公式,仿真结果与之存在一定偏差,仍然需要经过实际调试才能得到最佳性能。
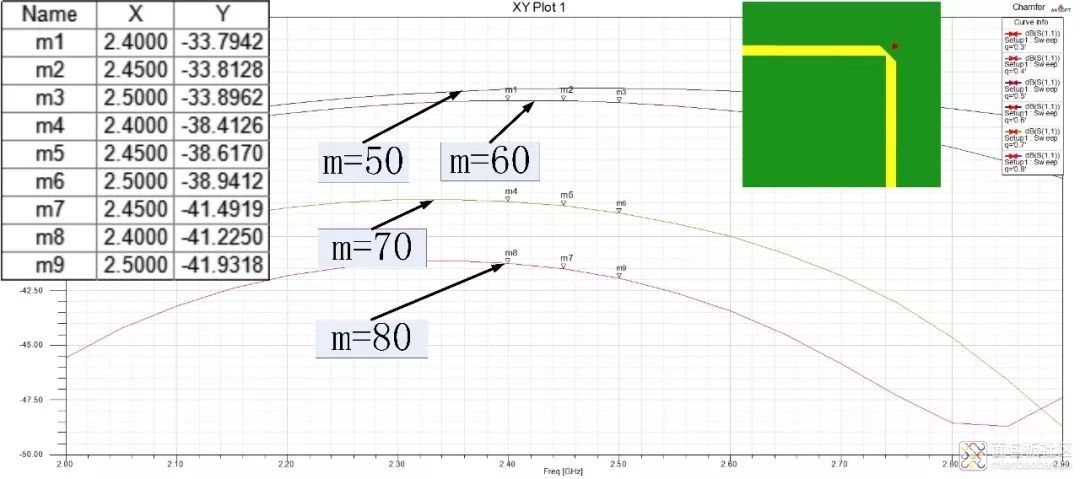
图8 直角弯曲45°外斜切仿真优化结果
文章开篇提出的另一个疑惑此时也迎刃而解:为什么选用3W规则?通过以上仿真分析和大量文献显示,“直角弯曲45°外斜切”法能获得更有优的性能,但是需要仿真结合实际调试才能达到期望的效果,过程相对较为繁杂耗时。对性能要求不高的场合,多数人会选择“3W规则”,加快项目进度。毕竟,时间就是金钱。
用反射抵消反射
微带线不连续导致信号反射大,“3W规则”和“直角弯曲45°外斜切”两种方案作为补偿措施,并没有完全达到直线的性能。我们对技术的探索、对细节的深究是不是就只能到此为止了呢?
矛盾总是有两面性的,我们是否可以利用矛盾抵消矛盾,利用反射抵消反射呢?于是,我们从传输线多次反射的观点[7]出发,提出一种拐角结构,通过两次转折,产生两次反射,期望能够利用反射抵消反射。结构如图9所示,该结构且由小编命名为“双转折”,其中Γ1是第一处转折的反射系数,Γ2是第二处转折的反射系数,θ是两处转折之间的传输线相位,为了作图方便,在仿真中以长度L代替,W是线宽,除了转折处,微带线其他各处宽度均为W,并与以上仿真中的W值(0.484mm)保持一致。
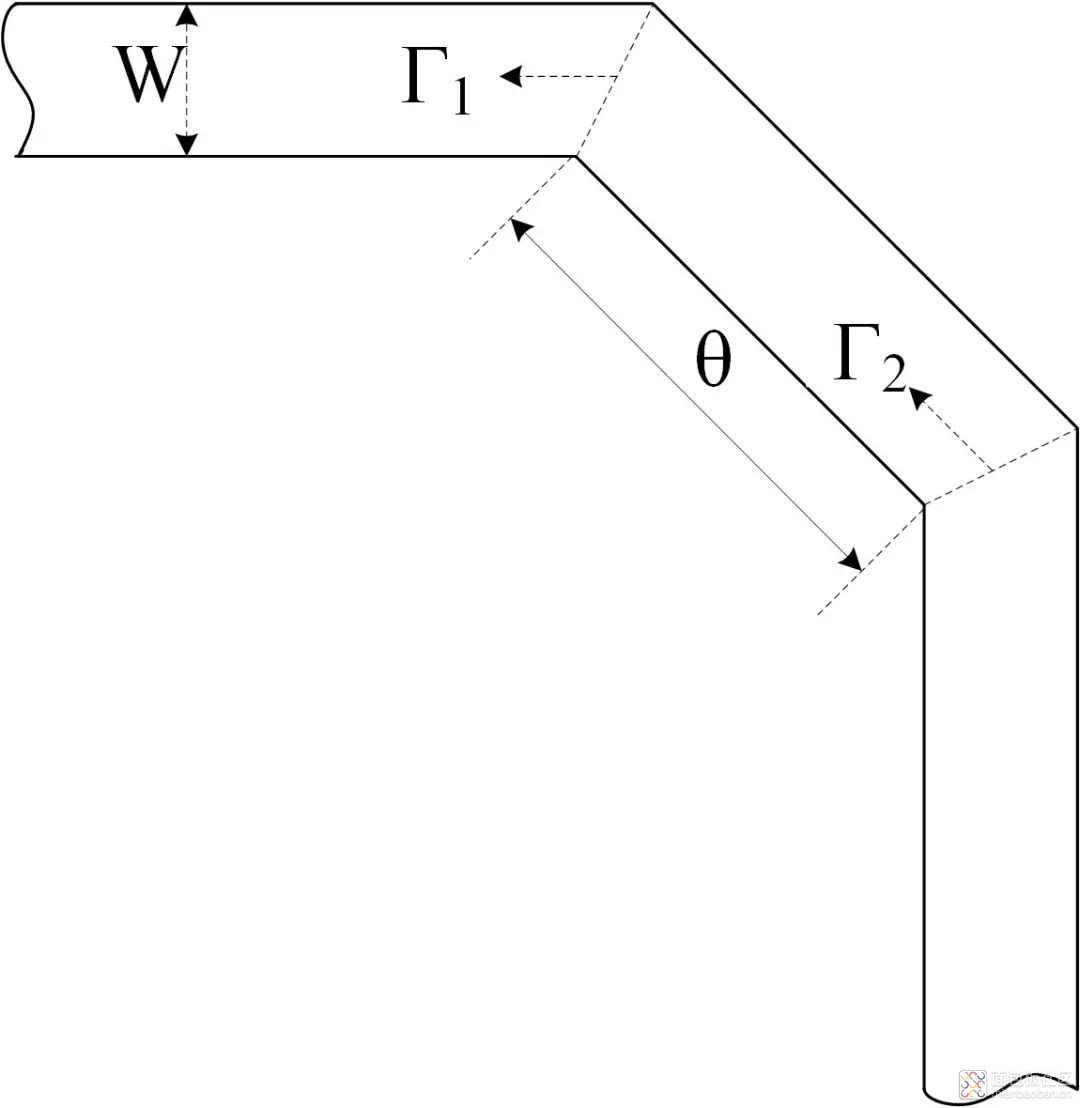
图9 双转折结构示意图
通过仿真调试优化,当L=10mm时,S11=-42.6dB,达到最小,几乎等同于直线时的性能。比“3W规则”提高了约8dB,比“直角弯曲45°外斜切”法提高了约2dB。仿真结果如图10所示,性能对比表见表1。
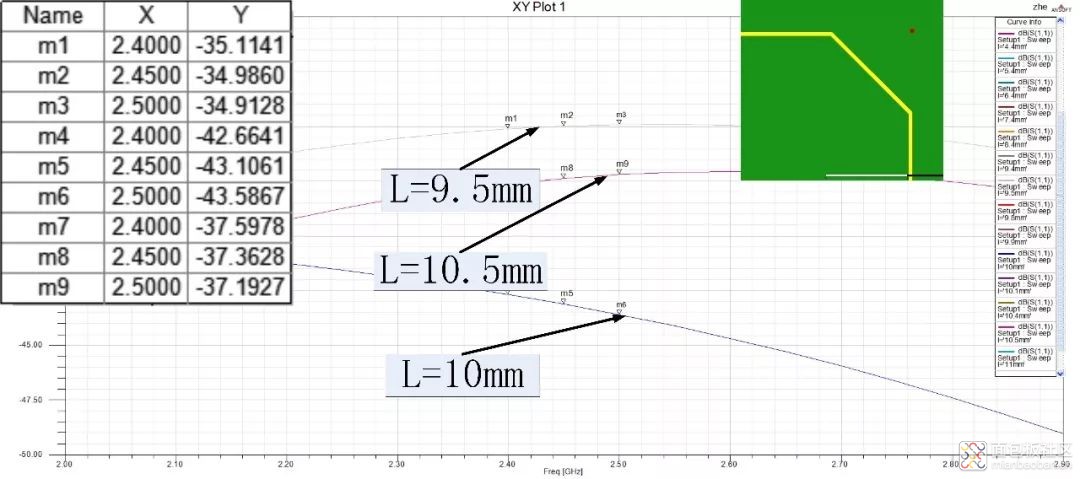
图10 双转折仿真优化结果
表1 微带线拐弯方案性能对比表
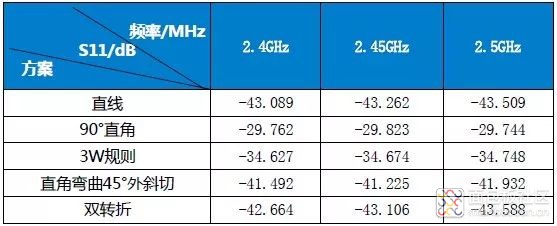
利用反射抵消反射的方法进行的设计案例还有很多,例如阶跃阻抗滤波器和波导法兰盘[2]。
好了,最后我们来总结一下
微带线不连续性的解决方案中,“3W规则”虽然不是性能最优的方案,但在实际应用中,由于其不需要进行详细仿真与调试优化,节约了开发时间,因此,在对性能要求并非特别严格的场合,依然是最便捷的选择。“直角弯曲45°外斜切”不仅能得到十分优良的性能,而且能节约PCB空间,在有条件进行仿真并实际调试的情况下,推荐使用此种方案。“双转折”方案,虽然能得到与直线相媲美的性能,但由于其仿真调试难度大,且占用空间,并不是十分推荐。
来源:ZLG致远电子






 /5
/5 

