在混合信号应用中，正确地选择驱动模数转换器 (ADC) 的运算放大器至关重要。设计人员 必须要对一些问题进行权衡，例如：放大器噪声、带宽、设置时间、ADC 信噪比 (SNR) 的 压摆率、无杂散动态范围 (SFDR)、输入阻抗以及采样时间等等。本文专门对单电源环境中 噪声规范和运算放大器以及逐次逼近寄存器 (SAR) ADC 性能的匹配进行了论述。 放大器产生的噪声源自于输入差动级。每一个放大器的输入级都会产生晶体管器件噪声， 其点噪声曲线图描述了参考输入端 (RTI) 噪声。利用这一图形信息，通过计算出参考输出 端 (RTO) 放大器噪声我们就可以确定 ADC 输入端产生了多少噪声。

　　该讨论首先从对放大器器件噪声的描述开始。随后，将放大器噪声源和一个性能系数联系 在一起，同时将一些单位从伏特转换为以分贝表示的 SNR。终，通过计算出运算放大器 SNR 值与 ADC SNR 性能的组合值就可以得出该混合信号电路（请参见图 1）中运算放大器 所产生的影响。

　　放大器噪声的特点

　　了解本应用中运算放大器产生的噪声是非常重要的。放大器的产品说明书中给出的典型性 能显示，运算放大器的过频率噪声性能具有明显的特征（请参见图 2）。本文中，由于我们 考虑到使用单电源 CMOS 放大器的一些影响，因此输入电流噪声非常低，以至于我们可以 将其忽略不计。这里，我们将只考虑放大器电压噪声的影响。

　　在典型的放大器产品说明书中，放大器噪声规范为一种 RTI 规范。我们可以在放大器的非 反相输入端将放大器噪声量化为一个电压源。运算放大器的电气特征表给出了输入电压噪 声和输入电压噪声密度规范（请参见图 2）。输入电压噪声规范 (10μVPP) 在带宽方面对 放大器的低频噪声作了描述。该带宽是放大器 1/f 噪声区域的一个组成部分。放大器输入 级中的晶体管以及输入级有源负载共同产生了这种噪声。

　　输入电压噪声密度会引起一个频率的噪声系数。例如，图 2 中的电气特征表显示，在 10 kHz 下的输入电压噪声密度 (end) 为 通常，该规范出现在频率曲线的宽带噪 声部分（请参见图 2）。从理论上来讲，这种宽带噪声是平坦的。假设是这种情况，那么 平坦噪声就是对放大器性能的一种较好的*价。不管是扩散电阻器还是晶体管的源极和漏 极，运算放大器中的电阻器都是主要的宽带噪声源。

　　放大器说明书包含了一个典型的规范图表，其显示了输入电压噪声密度与频率的对应关系。 图 2 就是这类图表的一个例子。在本例中，输入电压噪声规范就是输入电压（即 0.1Hz 至 10 Hz 规定频率之间的噪声密度曲线）以下的区域。需要注意的是，该规范的单位为峰至 峰值。为了将其转换为一个 rms 值，只需将峰至峰值除以 6.6（业界标准峰值因数 [CF] ＝3.3）即可。

　　表 1 包含了用于将 rms 转换为峰至峰值（反之亦然）的典型 CF 值。为了估计峰至峰运 算放大器输出噪声电压，我们将 rms 输出电压乘以 2CF。为了估计 ADC 峰至峰输出比特 性能，可从 rms 规范中减去比特峰值因数 (BCF)。

　　表 1 用于将 rms 转换为峰至峰的峰值因数和比特峰值因数值

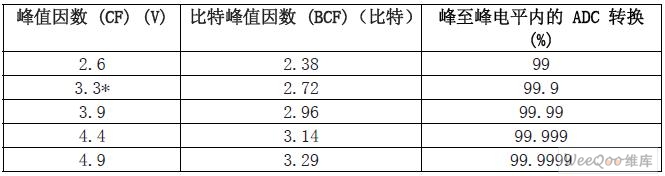
　　*业界标准的峰值因数

　　如图 2，我们可以非常容易地计算出中曲线以下部分，1/f 区域中不同输入电压噪声带宽 的噪声。在这一计算过程中，首先要确定 1 Hz 时的输入噪声密度。一旦我们得出该值， 下面简单的公式便会给出曲线以下的 rms 噪声。

　　我们在考虑这些低频噪声的时候，可能会立即得出这样的结论：我们应该将这种公式用到 非常低的频率中，例如：0.0001 Hz （0.0001 Hz = 每 2.8 小时 1 个周期）。但是，在 低于 0.1 Hz 的频率下，则每 10 秒钟一个周期，在电路中极有可能会出现其他情况，例 如：温度、老化程度或组件寿命等发生变化。实际上，来自放大器的低频噪声可能不会出 现在这种采样速度下，但是电路中可能会出现一些变化（例如：温度或者电源电压等的变 化）。

　　放大器规范表（请参见图 2）还给出了输入噪声密度值。该规范始终工作在较高的频率下， 即在输入电压噪声相对稳定的区域中。就这一曲线区域而言，乘以带宽的平方根和噪声密 度使噪声穿过该带宽。例如，如果放大器噪声在 10 kHz 下为 ，那么 6 kHz 到 100 kHz 带宽的放大器噪声则为：

　　其中，BW 等于相关带宽。

　　那么，我们如何从厂商的图表中得到一个 RTO 噪声值呢？我们可以计算出噪声曲线以下部 分的面积，然后乘以放大器的噪声增益。本例中，电路的噪声增益为+1 V/V。我们首先确 定放大器在两个区域中的噪声，然后使用平方和的平方根将这两个值加起来。图 3 显示了 进行这一计算的公式，并阐明了这两个区域。

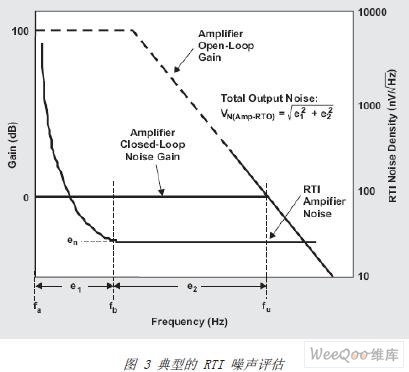
　　图 3 将噪声分为两部分。在区域 e1 中，通过放大器电路的 dc 增益，我们得到了值为 +1 V/V 的放大器 1/f 噪声。放大器噪声的这些规范为几纳伏/赫兹平方根。因此，只有当将 那个区域的带宽平方根乘以这个区域的平均噪声时，该分析才算完成。就 CMOS 放大器而 言，1/f 区域通常为从 0.1 Hz 至 100 Hz，甚至可以高达 1000 Hz。由于这一噪声值被带 宽平方根相乘，因此其产生的噪声较低。在区域 e2 中，放大器的宽带噪声被放大器电路增益（还是 +1 V/V）和带宽平方根相乘。

　　利用 TI 的 SPICE 仿真工具 TINA-TITM，我们可以验证这一噪声计算的正确性。请登录www.ti.com.cn/amplifier 查找该工具。

　　图 4 中的两个曲线图展示了 TINA-TI 如何帮助我们了解电路中的噪声。图 4 (a) 显示了 一个放大器的仿真噪声响应。图4 (b) 显示了频率增加时的累积噪声。需要注意的是，在 图 4 (b) 中，该噪声在较低频率下时非常低，这是因为，较低带宽被一个小数（即带宽） 的平方根相乘。当频率增加时，累积噪声也随之增加。有人会认为，由于图 4 (a) 的特点， 在较高频率下噪声的增加会更少。正如我们所看到的一样，并非如此，因为带宽乘法器（带 宽的平方根）在高频时更大。

　　将运算放大器与 ADC 噪声系数组合

　　我们检查放大器可能存在的噪声源时，可以较为容易地估计出图 1 中系统的总噪声。该系 统使用 16 位 ADC，即 ADS8325，其采样率为 100 ksps。这种器件的典型 SNR 为 91正如我们之前所看到的那样，OPA363 RTO 噪声为 109.8 dB。现在，通过使用运算放大器 SNR 和 ADC SNR，并运用平方和的平方根法则，我们就可以确定该系统的总体噪声了。

　　从这一计算，我们可以看到放大器噪声对系统精度具有非常小的影响。

　　利用电路中的这些器件，SNR 性能将总是等于或者小于值。假定在放大器和 ADC 之间 存在这种相互关系，那么选择一个更高噪声的放大器将得到差的结果。例如，如果我们 使用一个 10 V/V 增益的放大器，其在 10 kHz 下的典型电压噪声规范为 end=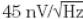 ， 那么 SNRTotal 为 82.2 dB。如果我们使用 16 位 ADS8325，那么 SNRTotal 则为 81.6 dB。在 本例中，放大器决定了电路噪声的高低。

　　还有更多影响放大器选择过程的因素，但是放大器噪声能够对数字编码结果产生巨大的影 响。如果放大器的噪声太大，那么 ADC 肯定会将放大器电路的噪声转换成数字输出。另一 方面，ADC 可能会比放大器电路的噪声更大。如果我们在没有*估系统的情况下选择一款 噪声极低的放大器，那么我们可能会在一个组件或者其他组件上花费太多的资金。确定一 个电路中潜在的噪声一直都是一个巨大的挑战，但是有一些经验法则是可以被用来克服这 些问题的。基于我们在计算方面的优势，我们可以利用电路的频率范围；另外，当我们组 合噪声源时，我们可以利用这一方程式来对平方和的平方根求解。通过使用这些技巧，我 们可以迅速地确定放大器/ADC 组合的一致性。

　　在本电路中，一个放大器将信号链阻抗隔离。我们可以添加其他一些特性，例如：增益或 滤波；但是无论我们在放大器周围添加了什么特性，我们都应该始终确保放大器电路能够 保持 ADC 的完整性。